TOPSIS法用于研究与理想方案相似性的顺序选优技术,通俗理解即为数据大小有优劣关系,数据越大越优,数据越小越劣,因此结合数据间的大小找出正负理想解以及正负理想解距离,并且在最终得到接近程序C值,并且结合C值排序得出优劣方案排序。
-
TOPSIS分析通常包括以下五步。
-
第一步:准备好数据,并且进行同趋势化处理(需要研究者自行处理);
-
第二步:数据归一化处理解决量纲问题(数据处理->生成变量,通常选择‘平方和归一化’);
-
第三步:找出最优和最劣矩阵向量(SPSSAU自动处理);
-
第四步:分别计算评价对象与正理想解距离D+或负理想解距离D-;
-
第五步:结合距离值计算得出接近程序C值,并且进行排序,得出结论。
-
特别提示:
-
针对第1步:数据一定需要全部同趋势正向化,即让所有的数据表示为数字越大越优(如果某指标项数字越大反而越劣,可使用数据处理->生成变量功能的逆向化/倒数功能进行处理);
-
特别提示:TOPSIS法对于数据格式要求严格,请参考下表格:
| 煤矿 | 粉尘浓度 | 二氧化硫量 | 肺病患病率 |
| 煤矿1 | 50.8 | 4.3 | 8.7 |
| 煤矿2 | 200.0 | 4.9 | 7.2 |
| 煤矿3 | 71.4 | 2.5 | 5.0 |
| 煤矿4 | 98.5 | 3.7 | 2.7 |
| 煤矿5 | 10.2 | 2.4 | 0.3 |
-
上表格为TOPSIS法的数据格式要求,当前有5个煤矿关于“粉尘浓度”,“二氧化硫量”和“肺病患病率”共3个指标数据;希望通过TOPSIS法对比5个煤矿的优劣性。数据中“粉尘浓度”,“二氧化硫量”和“肺病患病率”共3个指标,数值越大越劣,明显的需要进行数据同趋势正向化处理。这里直接对数据全部求倒数处理,即进行正向化处理。同时在第二步量纲化处理上,通常选择为‘平方和归一化’(SPSSAU数据处理->生成变量功能里面有)。
SPSSAU分析结果表格示例如下:
| TOPSIS评价计算结果 | ||||
| 项 | D+ | D- | C | 排序结果 |
| 评价对象1 | 1.256 | 0.150 | 0.107 | 3 |
| 评价对象2 | 1.353 | 0.007 | 0.005 | 5 |
| 评价对象3 | 1.246 | 0.291 | 0.190 | 2 |
| 评价对象4 | 1.252 | 0.131 | 0.094 | 4 |
| 评价对象5 | 0.000 | 1.358 | 1.000 | 1 |
-
特别提示:
-
上表格中第1列‘项’,是由SPSSAU默认生成的;
TOPSIS法案例
-
1、背景
有5个煤矿关于“粉尘浓度”,“二氧化硫量”和“肺病患病率”共3个指标数据;希望通过TOPSIS法对比5个煤矿的优劣性。原始数据如下:
煤矿 粉尘浓度 二氧化硫量 肺病患病率 煤矿1 50.8 4.3 8.7 煤矿2 200.0 4.9 7.2 煤矿3 71.4 2.5 5.0 煤矿4 98.5 3.7 2.7 煤矿5 10.2 2.4 0.3 2、理论
TOPSIS有两点需要特别注意,一是数据需要全部同趋势正向化,即数据一定需要越大代表越优(如果不是,则需要数据处理->生成变量功能的逆向化/倒数功能进行处理),本例子明显的数据越大越劣,因此首先使用【数据处理->生成变量】的倒数功能处理,让数据越大代表越优,并且使用倒数后的数据进行分析。接着还对数据进行量纲化处理,使用‘平方和归一化’(数据处理->生成变量),TOPSIS分析一般分为五步分别为:
-
第一步:准备好数据,并且进行同趋势化处理(需要研究者自行处理);
-
第二步:数据归一化处理解决量纲问题(数据处理->生成变量,通常选择‘平方和归一化’);
-
第三步:找出最优和最劣矩阵向量(SPSSAU自动处理);
-
第四步:分别计算评价对象与正理想解距离D+或负理想解距离D-;
-
第五步:结合距离值计算得出接近程序C值,并且进行排序,得出结论。
3、操作
本例子中需要首先对数据求倒数,使用【数据处理->生成变量】的倒数功能处理,接着第2步进行量纲操作(数据处理->生成变量,通常选择‘平方和归一化’),然后再进行分析,分别操作如下。
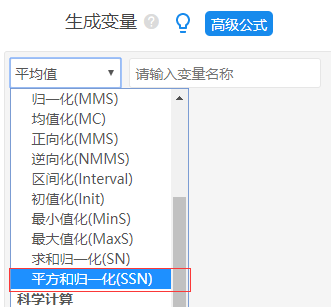
4、SPSSAU输出结果
TOPSIS评价计算结果 项 D+ D- C 排序结果 评价对象1 1.256 0.150 0.107 3 评价对象2 1.353 0.007 0.005 5 评价对象3 1.246 0.291 0.190 2 评价对象4 1.252 0.131 0.094 4 评价对象5 0.000 1.358 1.000 1 -
特别提示:
-
上表格中第1列‘项’,是由SPSSAU默认生成的,其分别代表煤矿1,煤矿2,煤矿3,煤矿4和煤矿5
5、文字分析
TOPSIS评价计算结果 项 D+ D- C 排序结果 评价对象1 1.256 0.150 0.107 3 评价对象2 1.353 0.007 0.005 5 评价对象3 1.246 0.291 0.190 2 评价对象4 1.252 0.131 0.094 4 评价对象5 0.000 1.358 1.000 1 -
特别提示:
-
上表格中第1列‘项’,是由SPSSAU默认生成的,其分别代表煤矿1,煤矿2,煤矿3,煤矿4和煤矿5
从上表可知,针对3个指标(“粉尘浓度”,“二氧化硫量”和“肺病患病率”,进行TOPSIS评价,同时评价对象为5个(样本量数量即为评价对象数量,这里是指5个煤矿);
TOPSIS法首先找出评价指标的正负理想解值,接着计算出各评价对象分别与正负理想解的距离值D+和D-。
根据D+和D-值,最终计算得出各评价对象与最优方案的接近程度(C值),并可针对C值进行排序。具体针对排序来看,评价对象5(煤矿5)最优,其次是评价对象3(煤矿3),而评价对象2(煤矿2)最劣。
6、剖析
-
特别提示
-
TOPSIS法对于数据格式要求严格,请按照事例进行;
-
数据一定需要全部同趋势正向化,即让所有的数据表示为数字越大越优(如果某指标项数字越大反而越劣,可使用数据处理->生成变量功能的逆向化/倒数功能进行处理)。
疑难解惑
-
提示“数据质量异常”?
-
如果原始数据中某一列完全相等,此时SPSSAU无法进行‘归一化’处理【公式为:(X-Min)/(Max-Min) 】,明显的,最大值和最小值相等,被除数为0,因此会提示此错误。可通过描述分析进行检查后,将该类数据移除出去再进行分析即可。
-
TOPSIS (也称DTOPSIS)法时各指标代表的意义?
-
A+和A-值,此两值分别代表评价指标的最大值,或者最小值(即最优解或最劣解);此两值用于计算D+或D-值使用,此两值大小并无太多意义。
-
D+和D-值,此两值分别代表评价对象与最优或最劣解(即A+或A-)的距离(欧式距离),此两值的实际意义是,评价对象与最优或最劣解的距离,值越大说明距离越远,研究对象D+值越大,说明与最优解距离越远;D-值越大,说明与最劣解距离越远。最理解的研究对象是D+值越小同时D-值越大。
-
相对接近度C值,C = D- / (D+ + D-),计算公式上,分子为D-值,分母为D+和D-之和; D-值相对越大,则说明该研究对象距离最劣解越远,则研究对象越好;C值越大说明研究对象越好。
-
是否需要对数据量表化(标准化/归一化等)进行处理?
-
如果说数据的单位并不统一,此时可进行量纲化处理,常用的处理方式为标准化,归一化,均值化等等。当具体针对TOPSIS法,‘平方和归一化’这种无量纲化处理方式使用较多。
-
是否需要对数据正向化/逆向化进行处理?
-
如果说原始数据有的指标为正向,有的为负向(逆向)指标;通常需要首先进行方向的统一,全部统一为正向指标。
-
正向/逆向化的处理方式多样并不固定,比如负向指标可求倒数,此时即把数据负向指标正向化了。建议可直接使用SPSSAU的数据处理->生成变量里面有单独的‘正向化’或者‘逆向化’处理选项即可。还有很多统一指标方向的处理方式,并不固定,目的均在于将指标的方向全部统一化。
-
如果使用SPSSAU的数据处理->生成变量中‘正向化’或者‘逆向化’处理选项,此数据已经进行过无量纲化处理,可以不再进行无量纲处理。
-
为什么分析样本量小于实际样本量?
-
如果分析时出现‘分析样本量’小于样本量,有3种可能。1是免费版(免费版仅分析前100行数据);2是做过‘筛选样本’功能(即主动设置只分析其中一部分数据);3是原始数据中有缺失数据(系统右上角‘我的数据’处可查看原始数据,也可下载原始数据等)。
-
TOPSIS法里面的权重参数是什么意思??
-
如果说进行TOPSIS分析时,各个指标有着权重属性(当然通常情况并没有),那么可对应设置各个指标的权重(输入的权重值可以为相对数字,SPSSAU默认都会进行归一化处理让权重加和为1),在进行D+和D-值计算时,SPSSAU会对应乘上权重值(如果没有权重则下述公式中权重值为1),计算公式如下:
-
-
分析结果中提示“预览前100项数据结果”?
-
SPSSAU中进行某些分析时,比如vikor/灰色关联法/topsis/熵权topsis/耦合协调度/综合指数时,并且分析样本量过大导致需要输出非常多结果时,此时结果仅输出前100项数据结果进行预览。此时可通过以下两步得到全部结果。
-
第1步:在‘开始分析’按钮右侧选中‘保存结果值’,系统将指标值存储在原始数据文档中,并且以不同的标题名称进行标识;
-
第2步:分析完成后,右上角‘我的数据’下载该数据文档,即将全部数据下载出来使用。
