Mood中位数检验案例

• 1、背景

  当前希望比较三种不同教学方法对学生学习效果的影响，即数据包括教学方法（传统教学、多媒体教学、小组合作），研究项分别是数学成绩（0-100分）、阅读成绩（0-100分）和专注时间（分钟），每组20个学生，共计20*3=60行数据，其数据格式类似下图：

  

  当前希望检验三种教学方法在数学成绩，阅读成绩和专注时间共3项上的中位数是否存在显著差异，以用于教育决策提供数据依据。本案例时，由于各组数据较少仅20个，因而数据较难呈现出正态性，而且成绩这类数据也有可能出现异常（比如某学生仅几分），与此同时，使用中位数来表示成绩等信息的整体水平情况也较为适合，因而使用Mood中位数检验较为适合。

• 2、理论

  Mood中位数检验的核心思想是通过比较各组数据相对于总体中位数的分布模式来判断组间差异。Mood中位数检验的假设为：零假设H₀： 各组的总体中位数相等 备择假设H₁： 至少有两个组的总体中位数不相等。其具体计算步骤如下：

  第一步：计算总体中位数

  将所有组的数据合并，计算总体中位数M：

  第二步：构建列联表

  对每个组i，统计低于和高于总体中位数的观察值个数：A_i = 组i中 ≤ M 的观察值个数，B_i = 组i中 > M 的观察值个数，n_i = A_i + B_i（组i的总样本量）。

  第三步：计算检验统计量

  Mood检验使用卡方统计量来衡量观察频数与期望频数的偏离程度，χ² = Σ_i=1^k Σ_j=1² (O_ij - E_ij)² / E_ij，其中：O_ij 是第i组第j列的观察频数，E_ij 是第i组第j列的期望频数，关于期望频数计算上：E_i1 = n_i × A / N （组i中期望的≤M个数），E_i2 = n_i × B / N （组i中期望的>M个数）。

  除此之外，检验统计量的自由度df = k - 1（k为组数），在零假设成立且样本量足够大的条件下，卡方统计量近似服从自由度为(k-1)的卡方分布。结合卡方统计量和df值计算出p 值。

• 3、操作

  本例子操作截图如下：

  

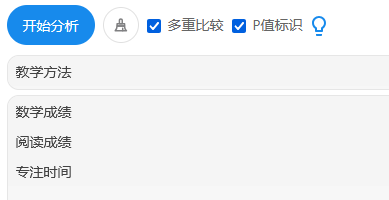
  分别将教学方法放入X框，另外3项放入Y框中。并且默认选中‘多重比较’和‘P值标识’。

• 4、SPSSAU输出结果

  SPSSAU共计输出3类表格和两类图形，分别是描述性统计量、Mood中位数检验结果，Mood检验多重比较结果，柱形图差异对比和可视化P值差异对比。描述性统计量展示各组别基本的中位数，小于或者大于中位数的样本个数信息等，Mood中位数检验结果展示最终假设检验结果，并且通过Mood检验多重比较结果展示两两比较的结果。以及使用两类图形来展示具体差异情况。

• 5、文字分析

  

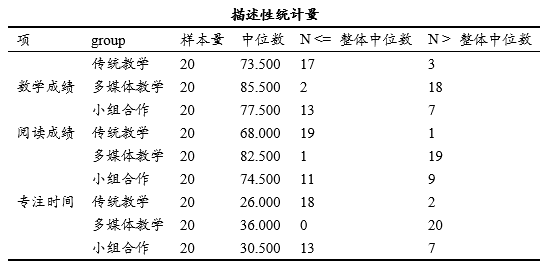
  上表格展示Mood中位数检验的基本统计量信息。包括各个组别时的样本量、中位数指标信息，以及展示各个组别时，数据小于整体中位数或数据大于整体中位数的样本量，当数据呈现出显著性差异时，可具体对比中位数值来描述差异情况。

  

  上表格展示Mood中位数检验的结果；Mood中位数检验适用于数据不满足正态分布且有异常值的情况，反之如果不符合上述特征时，建议使用非参数参数或者方差分析进行研究；如果对应的p 值小于0.05，则意味着拒绝原假设（原假设为各组别中位数相等），即说明各组别中位数不相等，反之则说明各组别中位数无明显差异。

  从上表格可以看到：3种教学方法对于数学成绩、阅读成绩和专注时间均呈现出显著性差异，也即说明不同教学方法时，成绩和专注时间均有着明显的不同。具体进一步可对比差异情况，可直接通过‘描述性统计量’进行描述，比如多媒体未定时数学成绩的中位数（即整体水平）为85.5，并且多媒体教学时阅读成绩明显更高，中位数值为82.5分，与此同时，专业时间也在多媒体教学时表现出最高水平，中位数值为36分钟。与此同时，还可进行两两比较，也即研究3种教学方式的任意两种之间的差异对比，如下表格所示：

  

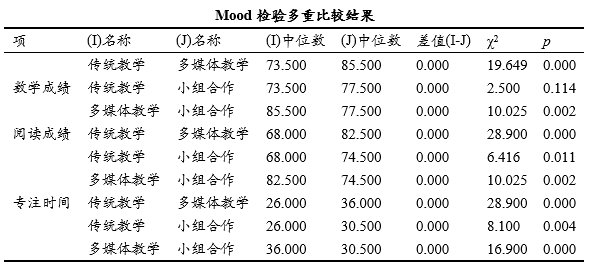
  事后检验(多重比较)对比具体两两组别的差异性，需要注意的是，其前提是Mood检验呈现出显著性，比如本案例时数学成绩、阅读成绩和专注时间均呈现出显著性，因而可进一步使用‘多重比较’结果。上表格展示与各组别对应的中位数，以及中位数差值情况和统计量信息等。

  具体多重比较时，建议需要进行Bonferroni校正，比如显著性水平为0.05，并且两两比较次数为3次，那么Bonferroni校正显著性水平为0.05/3次=0.0167，即p 值需要与0.0167进行对比，而不是0.05；具体来看，比如传统教学与多媒体教学的中位数分别是73.5和85.5，并且p 值为0.000，多数情况下该p 值应该与0.05（即0.05水平）进行对比，但Bonferroni校正时，显著性水平是0.05，但对比的p 值应该与0.05/3次=0.0167，在本例子中，Bonferroni校正差异对比时与0.0167对比（基于0.05显著性水平前提下），也依旧呈现出显著性。

  除此之外，还可使用可视化图直观展示差异情况情况，分别如下：

  

  

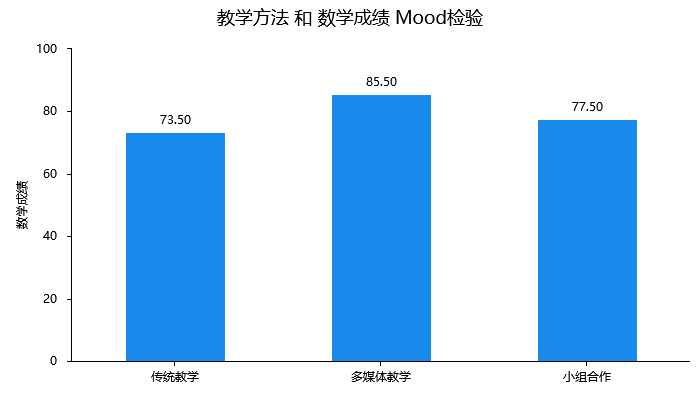
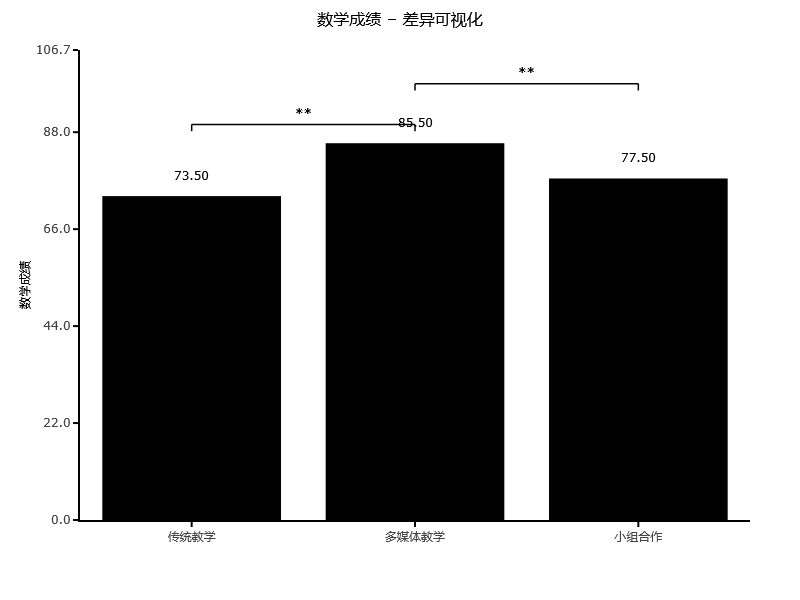
  上图可数学成绩的差异可视化，并且使用*号来标识，并且上图中对比的p 值已经进行过Bonferroni校正来使用，而并非直接使用表格里面的p 值。

• 6、剖析

  涉及以下几个关键点，分别如下：

  • 为什么我的检验结果显示"null"？

  • 如果Mood中位数检验结果显示为null值，可能原因有：①某些组样本量为1或0；②数据中缺失值过多等。

  • p 值很小但中位数看起来差不多？

  • 此情况是正常的，这可能是样本量很大导致。统计显著不等于实际重要，需要结合专业知识判断差异是否有实际意义。

  • 什么时候选择Mood检验而不是其他非参数检验？

  • 当研究时明确关心中位数差异，且数据存在偏态或异常值时，Mood检验是最适合的选择，与此同时也可使用非参数检验这一方法，其也是对非正态数据的差异研究方法。

  • Mood中位数检验时关于多重比较时Bonferroni校正？

  • 在SPSSAU中进行Mood中位数检验时，SPSSAU自动进行Bonferroni校正然后基于此结果进行可视化对比绘图使用，比如显著性水平为0.05，并且两两比较次数为3次，那么Bonferroni校正显著性水平为0.05/3次=0.0167，即p 值需要与0.0167进行对比后来展示*号情况。