Mann Kendall检验案例

• 1、理论

  1.1 基本理论

  Mann Kendall检验的基本原理建立在符号检验的基础上。对于时间序列X₁, X₂, ..., X_n，检验统计量S的计算方法是：

  • 对于所有可能的数据对(Xᵢ, Xⱼ)，其中i < j，计算符号函数：

  • 如果X_j > X_i，则sgn = +1

  • 如果X_j < X_i，则sgn = -1

  • 如果X_j = X_i，则sgn = 0

  最终的检验统计量S等于所有符号函数值的累积和，其用来衡量时间序列中单调趋势强度。如果时间序列存在上升趋势，S值会显著为正；如果存在下降趋势，S值会显著为负；如果没有明显趋势，S值会接近零。通过标准化处理，可以得到标准正态分布的z 统计量，进而计算p 值来判断趋势的显著性。这种方法的优势在于它只关注数据的相对大小关系，而不依赖于具体的数值分布特征。Mann Kendall检验的结果主要通过z 统计量和p 值来判断：p 值< 0.05则意味着存在显著趋势，反之则说明无明显趋势。当存在着显著趋势时，结合z 值判断是上升还是下降，当z > 0则说明是上升趋势，z < 0则说明是下降趋势。另外在SPSSAU中，共提供9种类型的Mann Kendall检验，如下述：

  检验类型	适用场景	推荐使用条件
  原始Mann Kendall检验	独立观测数据	数据点间相互独立
  Hamed-Rao修正	存在自相关的数据	短期自相关明显
  Yue-Wang修正	存在自相关的数据	长期自相关存在
  预白化Mann Kendall检验	强自相关数据	自相关结构已知
  无趋势预白化	既有趋势又有自相关	复杂时间序列
  多变量Mann Kendall检验	多个相关变量	多指标综合评估
  季节性Mann Kendall检验	具有季节性的数据	月度、季度数据
  区域Mann Kendall检验	多个站点数据	比如区域气候分析

  原始Mann Kendall检验：这是最基础的版本，适用于观测值相互独立的时间序列。它的假设条件是数据点之间没有自相关，这在实际应用中往往难以满足，特别是对于连续监测的环境数据。尽管如此，由于其计算简单、结果直观，仍然是趋势分析的首选方法。

  Hamed-Rao修正检验：当数据存在自相关时，原始Mann Kendall检验容易产生假阳性结果（即错误地检测出不存在的趋势）。Hamed-Rao修正通过调整方差计算公式来校正这种偏差。它特别适合处理短期自相关较强的情况，比如日降水量数据中连续几天的相关性。

  Yue-Wang修正检验：这种修正方法在处理长期持续性（长期记忆）方面表现更好。它不仅考虑了相邻观测值的相关性，还考虑了距离较远的观测值之间的相关性。对于气候数据中常见的长期周期性变化，这种方法相对更加可靠。

  预白化Mann Kendall检验：预白化是一种更激进的自相关处理方法。它首先建立自回归模型来描述数据的自相关结构，然后从原始数据中减去这种自相关成分，得到"白化"后的残差序列，再对残差进行Mann Kendall检验。这种方法在自相关结构已知且较强的情况下效果很好。

  无趋势预白化检验：这是预白化方法的改进版本。它认识到在有趋势的时间序列中，简单的预白化可能会错误地移除真实的趋势成分。因此，它采用迭代的方法，先估计趋势，再进行预白化，然后重新估计趋势，直到收敛。

  多变量Mann Kendall检验：当需要同时分析多个相关变量的趋势时，多变量Mann Kendall检验提供了一个综合的解决方案。例如，在分析某地区的环境变化时，可以同时考虑温度、湿度、降水量等多个指标，得出一个综合的趋势判断。

  季节性Mann Kendall检验：许多环境和经济数据都具有明显的季节性特征。季节性Mann Kendall检验通过分别计算每个季节（如每个月）内的趋势，然后综合所有季节的结果，有效地消除了季节性变化对趋势检测的干扰。

  区域Mann Kendall检验：当分析区域性的变化趋势时，比如整个流域的水质变化或某个地区的气候变化，区域Mann Kendall检验可以综合多个监测站点的数据，给出区域整体的趋势判断。这种方法假设所有站点具有相同的趋势方向，但允许趋势的大小有所不同。

  1.2 突变点检测

  在SPSSAU中还默认提供突变点检测，突变点检测是Mann Kendall检验的重要扩展应用，用于识别时间序列中发生显著变化的时间点。这在气候变化研究、环境监测、质量控制等领域具有重要意义。突变点检测基于累积距平的概念。对于时间序列的每一个时间点，计算从序列开始到该点的累积统计量，形成前向序列UF；同时，从序列末尾开始反向计算，形成后向序列UB。当UF和UB曲线相交时，交点对应的时间就可能是突变点。

  具体来说，UF序列反映了从序列开始到当前时刻的趋势强度，而UB序列反映了从当前时刻到序列结束的趋势强度。如果在某个时间点发生了突变，那么这个点之前和之后的趋势特征会发生明显变化，表现为UF和UB曲线的交汇。UF-UB交点检测法最为常用，与此同时，SPSSAU还提供其它两种方式，分别是均值突变法和统计显著性持续验证法。具体如下述：

  均值突变法：基于滑动窗口均值比较的突变检测方法，其核心思想是通过比较时间点前后的局部统计特征来识别突变，该方法假设如果在某个时间点发生了突变，那么这个点前后的数据统计特征（主要是均值和方差）会发生显著变化。此方法重点考察突然点的跳跃情况。

  UF-UB交点检测：经典的Mann Kendall突变点检测方法。通过计算正向和反向的累积统计量序列，寻找两条曲线在95%置信区间内的交点。这种方法的优势是有明确的统计学意义，交点的显著性可以通过置信区间来判断。此方法偏向于判断比如由升而降，或者由降而升的拐点。

  统计显著性持续验证法：趋势强度变化率的检测方法，专门识别趋势发生急剧变化的时刻。通过分析UF曲线的斜率变化来检测突变。如果UF曲线在某点的斜率发生剧烈变化，说明趋势的强度或方向发生了突然改变。此方法重点关注趋势强度变化，比如从缓慢上升转为快速上升。

  • 提示：

  • 突变点检验是Mann Kendall检验的进阶拓展应用，多数情况下并不需要考虑此点。而且对于突变点检验结果需要保持谨慎的态度，因而其对数据质量、时间序列长度等均有较多的要求，建议研究者结合实际数据情况进行综合判断和选择使用。

• 2、操作

  当前有一份长江中游某支流水质监测站1990-2023年的年度监测平均值数据，包括溶解氧浓度（毫克/升）和水温（摄氏度）两项数据，现希望使用Mann Kendall趋势分析历年来的温度趋势情况。本例子操作截图如下：

  

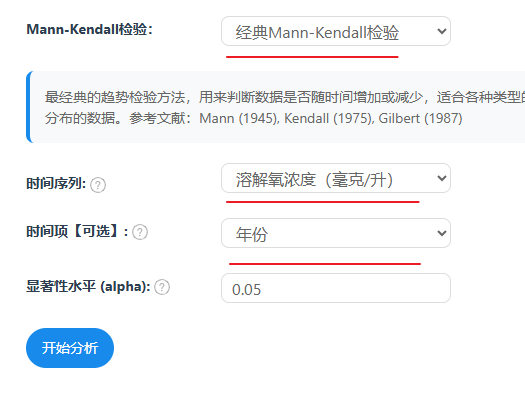
  默认使用经典的Mann Kendall检验方式，将水温项放入时间序列项中，显著性水平默认是0.05，也可修改为比如0.01或0.1等。时间项是可选项，其并不影响结果，但其影响到绘图时横坐标信息。如果不放入，那么SPSSAU默认数据从上到下的顺序展示。

• 3、SPSSAU输出结果

  SPSSAU输出3个表格和2个图，如下述：

  项	说明
  Mann Kendall检验参数信息	展示检验数据，显著性水平等基础信息
  Mann Kendall检验结果	核心检验结果表格，分析趋势性情况等结果
  Mann Kendall检验突变点	展示突变点的检测结果表格
  突变点检测	展示突变点情况
  UF/UB统计量	展示UF/UB统计图

  Mann Kendall检验参数信息
  项	值
  检验类型	经典Mann Kendall检验
  显著性水平	0.050

  针对Mann Kendall检验，绝大多数情况下使用经典Mann Kendall检验类型即可，如果考虑处理自相关问题，可考虑‘预白化Mann Kendall检验’或者‘无趋势预白化Mann Kendall检验’；如果考虑季节性，可使用‘季节性Mann Kendall检验’或‘相关季节性Mann Kendall检验’；如果是同时考虑多个时间序列，可使用‘多变量Mann Kendall检验’或‘相关季节性Mann Kendall检验’；‘Hamed和Rao修正Mann Kendall检验’或‘Yue和Wang检验’时处理自相关性问题时，需要纳入lag滞后项参数，通常情况下为1即可。除此之外，默认显著性水平为0.05，也可考虑设置成比如0.01或0.1

  Mann Kendall检验结果
  项	值	说明
  z 值	7.531	检验统计量，用于计算p 值
  p 值	0.000	如果p 值<0.05则意味着有趋势，反之意味着无趋势
  趋势判断	上升趋势	结合p 值和z 值的正负号判断得到的结论
  Sen's 斜率	0.200	趋势的斜率估计值，大于0时意味着上长趋势，反之小于0为下降趋势，绝对值大小表示趋势强度
  截距值	15.650	趋势线的起点估计值，意义较小
  Kendall's tau值	0.907	时间和观测值之间的非参数相关系数，其介于[-1,1]之间，大于0时意味着上长趋势，反之小于0为下降趋势，绝对值大小表示关系强度
  Mann-Kendal's score	509.000	S统计量，其意义为后一个值大于前一个值的数量减去小于的数量
  方差	4550.333	用于衡量S统计量的波动强度，其意义相对较小

  1990~2023共34年的温度来看，该时间序列数据呈现出极其显著的上升趋势。检验的z 统计量为7.531，远超过95%置信水平的临界值1.96，同时p 值接近0.000<0.01即意味着温度有着明显的时间趋势，并且是上升趋势。

  从趋势强度来看，Kendall's tau系数达到0.907，接近1，说明数据点之间存在极强的单调递增关系，趋势的一致性和稳定性都很高。Sen's斜率估计值为0.200，这意味着在整个观测期间，数据每年平均增长0.200个单位，这种增长速度相对稳定且持续。Mann Kendall原始统计量S值为509.000，这个较大的正值进一步证实了数据的强烈上升趋势。

  综述：该温度时间序列表现出非常明显、统计上极其显著的单调上升趋势。

  Mann Kendall检验突变点
  类型	时间点	值

  SPSSAU共提供3种突变点探测，分别是均值突变、UF-UB交叉点法和统计显著性持续验证法；如果算法自动检测到突变点则会在表格中呈现。以及突变点并非固定式算法，建议仔细甄别判断。上表格显示并没有发现突变点，因而无数据，以及下述的图形也不会展示突变点。

  

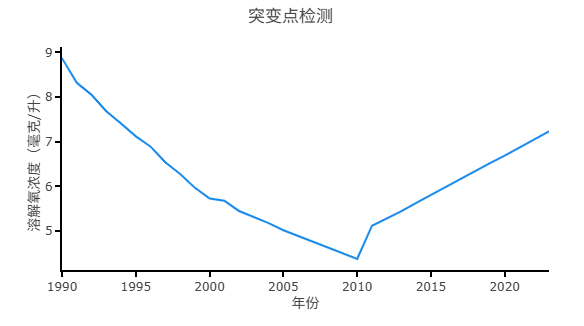
  上图直观展示原始数据序列及突变点，本案例并没有出现突变点，因而图中无展示。如果有突变点则会以红色圆点形式展示出来。

  

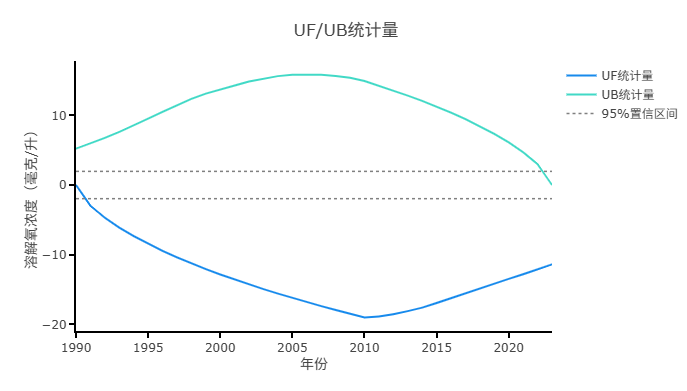
  • 针对UF统计量，UF值表示从序列起点开始，逐步累积的趋势变化情况，经过标准化处理后，其数值可以用于判断趋势的显著性：

  • UF > 0：表示序列在该时刻之前整体呈上升趋势。

  • UF < 0：表示序列在该时刻之前整体呈下降趋势。

  • UF ≈ 0：说明序列在该时刻之前没有明显趋势，变化较为随机。

  • UF 超过临界值（如 ±1.96）：表示趋势达到统计显著性，通常以95%置信度为标准。

  UF曲线的走势可以帮助我们识别趋势的开始时间。例如，UF持续由负转正，且超过显著性界限，说明序列可能在该时刻开始由下降转为上升。

  • 针对UB统计量，UB值是对时间序列从末尾向前计算的趋势统计量，反映的是从未来回看过去的趋势变化：

  • UB > 0：表示序列在该时刻之后整体呈上升趋势。

  • UB < 0：表示序列在该时刻之后整体呈下降趋势。

  • UB ≈ 0：说明序列在该时刻之后没有明显趋势。

  • UB 超过临界值（如 ±1.96）：表示趋势在该时刻之后达到统计显著性。

  UB的意义与UF刚好相反，但它的作用在于提供一个“回溯视角”，当UF和UB曲线在某一时刻交叉，并且该交点位于显著性区间之外，就可能是一个突变点。

  上图中从UF来看其基本全部均小于0，意味着从全局来判断，数据是呈现下降趋势的，以及UF的整体轮廓也展示出该数据的整体走势。类似地UB均在于0，意味着数据从后往前看，全局上是呈现出上长趋势，也即说明全局用一个词来概括的话数据是呈现下降趋势。另外，UB的轮廓走势是数据从后向前看的走势情况。

• 4、剖析

  涉及以下几个关键点，分别如下：

  • 应该选择哪种MK检验？

  • 在SPSSAU中，针对Mann Kendall检验，绝大多数情况下使用经典Mann Kendall检验类型即可，如果考虑处理自相关问题，可考虑‘预白化Mann Kendall检验’或者‘无趋势预白化Mann Kendall检验’；如果考虑季节性，可使用‘季节性Mann Kendall检验’或‘相关季节性Mann Kendall检验’；如果是同时考虑多个时间序列，可使用‘多变量Mann Kendall检验’或‘相关季节性Mann Kendall检验’；‘Hamed和Rao修正Mann Kendall检验’或‘Yue和Wang检验’时处理自相关性问题时，需要纳入lag滞后项参数，通常情况下为1即可。

  • 突变点检验的具体说明？

  • 在SPSSAU中默认提供突变点检测，突变点检测是Mann Kendall检验的重要扩展应用，共提供3种检测方法，其中UF-UB交点检测法最为常用，与此同时，SPSSAU还提供其它两种方式，分别是均值突变法和统计显著性持续验证法。需要说明的是，突变点检验是Mann Kendall检验的进阶拓展应用，多数情况下并不需要考虑此点。而且对于突变点检验结果需要保持谨慎的态度，因而其对数据质量、时间序列长度等均有较多的要求，建议研究者结合实际数据情况进行综合判断和选择使用。