箱线图(也称盒图,箱盒图等)是在1977年由美国统计学家John Tukey发明,分析数据需要为定量数据。通过箱线图,可以直观的探索数据特征。箱线图共有两个用途。分别如下:
-
直观地识别数据中异常值(离群点);
-
直观地判断数据离散分布情况,了解数据分布状态。
箱线图共由五个数值点构成,分别是最小观察值,25%分位数(Q1),中位数,75%分位数(Q3),最大观察值。需要特别说明的是,最小观察值和最大观察值定义如下:
-
最小观察值 = Q1 – 1.5(IQR), IQR = Q3 –Q1
-
最大观察值 = Q3 + 1.5(IQR), IQR = Q3 –Q1
-
如果数据有存在离群点即异常值,他们大于超出最大或者最小观察值,此时此将离群点以“圆点”形式进行展示。
-
箱线图中,‘下限’为最小观察值与真实最小值之间的较大值;‘上限’为最大观察值与最大值之间的较小值。
箱线图的使用场景情况如下:
-
查看可能的异常值数据情况(比如在回归分析前查看是否有异常数据);
-
非参数检验时查看不同类别X时,Y的数据分布情况;
-
其它涉及查看数据分布或者异常值查看时。
SPSSAU操作截图如下:
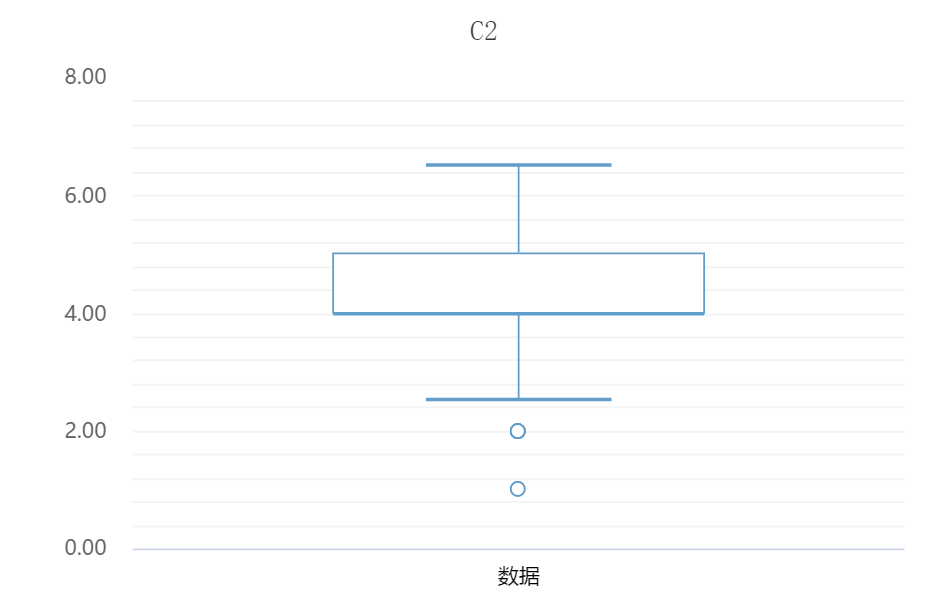
-
上图中直观展示出C2时共有2个异常值点,如果对C2进行分析,且分析方法对异常值敏感时(比如相关分析,回归分析等),此时需要对该2个异常值点进行处理成null或者填充(SPSSAU异常值功能),或者在分析时进行过滤。
-
特别提示
-
SPSSAU提供不同类别X时,Y的箱线图分布,比如上图中可以查看不同性别人群,C1,C2和C3共三项在区分性别时的盒状分布。
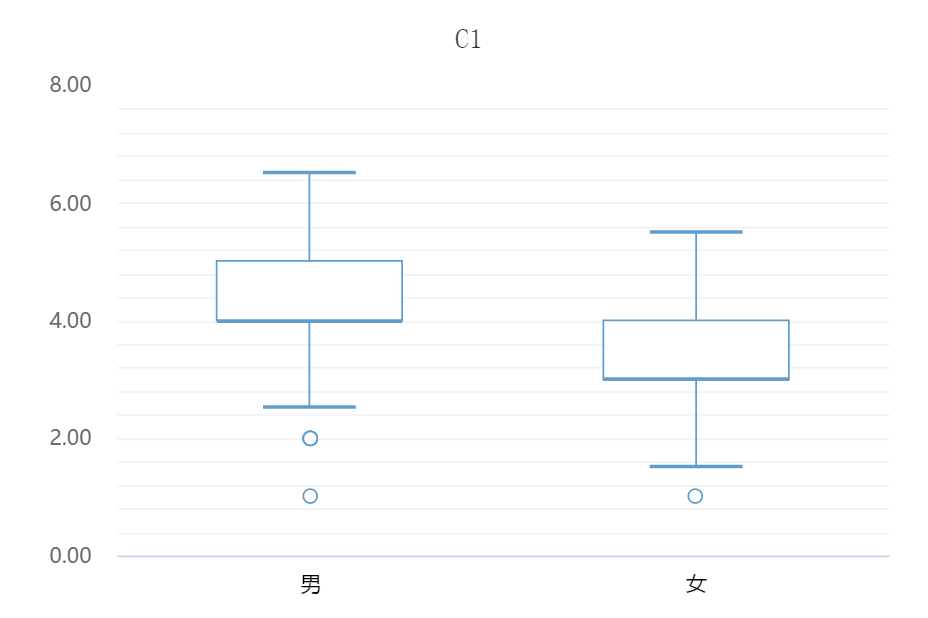
得到结果比如C1的箱线图如下:
-
上图可以看出,在男性时,C1中有2个异常点;女性时,C1共出现1个异常点。移动到异常点时会显示具体数据。此时如果有需要,可将此3个异常值进行处理,或者在分析时过滤掉异常值。
-
除了异常值的观察,还可以通过数据箱线图直观看出,男性在C1上的整体打分,会明显高于女性打分。
疑难解惑
-
极大值和极小值,最大值和最小值问题?
-
箱线图里面的极大值并非最大值,极小值也不是最小值。其计算公式为:最小观察值 =Q1 - 1.5(IQR), IQR = Q3 –Q1;最大观察值 =Q3 + 1.5(IQR), IQR = Q3 –Q1
