-
对于定量数据,比如量表评分(非常不满意,不满意,非常满意等),或者身高体重的值,可以通过描述性分析计算数据的集中性特征(平均值)和波动性特征(标准差值),同时SPSSAU系统还提供最大最小值,以及中位数值.描述性分析通常用于研究量表数据的基本认知情况分析,使用平均值去表述样本对于量表数据的整体态度情况。
分析项 描述分析说明 网购满意度 数字1代表非常不满意,2代表比较不满意,3代表一般,4代表比较满意,5代表非常满意;则可通过描述分析计算平均得分,描述整体满意情况如何。 分析结果表格示例如下(SPSSAU同时会生成折线图/雷达图等):
样本量 最小值 最大值 平均值 标准差 中位数 分析项1 198 1.57 5.00 3.43 0.76 0.76 分析项2 198 2.00 5.00 3.93 0.86 0.86 分析项3 198 2.00 5.00 3.84 0.90 0.90 分析项4 198 1.00 5.00 3.32 1.01 1.01 -
特别提示
-
描述性分析通常可用于 查看 数据是否有异常(最小值或最大值查看),比如出现-2,-3等异常等。
-
如果多个量表题表示一个维度,可使用“生成变量”的平均值功能。将多个量表题合并成一个整体维度。
同时SPSSAU会输出更多细节指标,如下表:
名称 方差 25分位数 中位数 75分位数 IQR 峰度 偏度 A1 0.728 4.000 4.000 5.000 1.000 0.482 -0.841 A2 0.585 4.000 4.000 5.000 1.000 2.317 -1.214 A3 0.683 4.000 4.000 5.000 1.000 0.630 -0.774 A4 0.905 3.000 4.000 4.750 1.750 -0.487 -0.474 -
上表格中指标使用情况相对较少,25分位数是指有25%的点低于该值;类似还有中位数代表有50%的点低于该值,75分位数代表有75%的点低于该值。
-
IQR等于75分位数 – 25分位数,表示数据集中情况。
-
峰度和偏度通常用于判断数据正态性情况,峰度的绝对值越大,说明数据越陡峭,峰度的绝对值大于3,意味着数据严重不正态。同时偏度的绝对值越大,说明数据偏斜程度越高,偏度的绝对值大于3,意味着严重不正态(可通过直方图查看数据正态性情况)。
-
除了使用描述性分析外,SPSSAU也建议用户可使用箱线图直观展示数据分布情况。
SPSSAU操作截图如下:
-
疑难解惑
-
提示“SPSSAU建议使用中位数进行描述分析,而不是使用平均值”
-
描述分析通常分析数据的整体水平情况,通常是使用平均值概括整体水平情况。试想一组身高数据,大部分都是1.7米,但突然出来一个2.2的异常值,一下子就拉高整体水平。此时再使用平均值表示整体身高水平,显得不合适,而应该使用中位数(即原始数据排序后最中间那个数字)表示整体身高水平更为适合。
-
如何计算众数?
-
众数是指出现频率最高的项,建议使用频数分析查看即可。有可能出现频数出现最高的项有多个,此时众数就有多个。众数的实际应用意义较少,建议用户可结合数据类型情况,使用百分比,或者平均值或者中位数等,而不使用众数。
-
排序题如何分析?
-
排序题一般是计算平均排名值,通过排名大小进行对比和分析。直接使用描述分析即可,同时排序题也是‘定量’数据,可使用方差分析或t检验等对比排名的差异情况。特别提示,需要注意数字代表的意义,比如数字越小代表排名越好,还是数字越大代表排名越好。如果数字大小代表的排名好坏与从预期不符,建议可使用数据处理里面的数据编码进行反向处理后再分析即可。
-
描述分析中缺失分析说明?
-
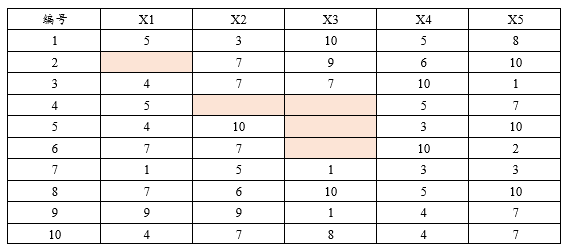
如下图所示:共有10个样本数据,但是X1,X2和X3有不同程度的缺失数据。比如将X1~X5共5项纳入进行比如线性回归分析时,其只会分析该5项均有完整数据,即第1/3/7~10共计6行数据(此6行称为‘全局过滤后样本量’)。而第2/4~5共4行数据有不同程度的缺失,因而不会纳入分析范畴。很多分析方法均需要保证数据具有完整性,SPSSAU会自动过滤数据确保符合算法要求,并且在分析结果中输出真实分析样本数据。