-
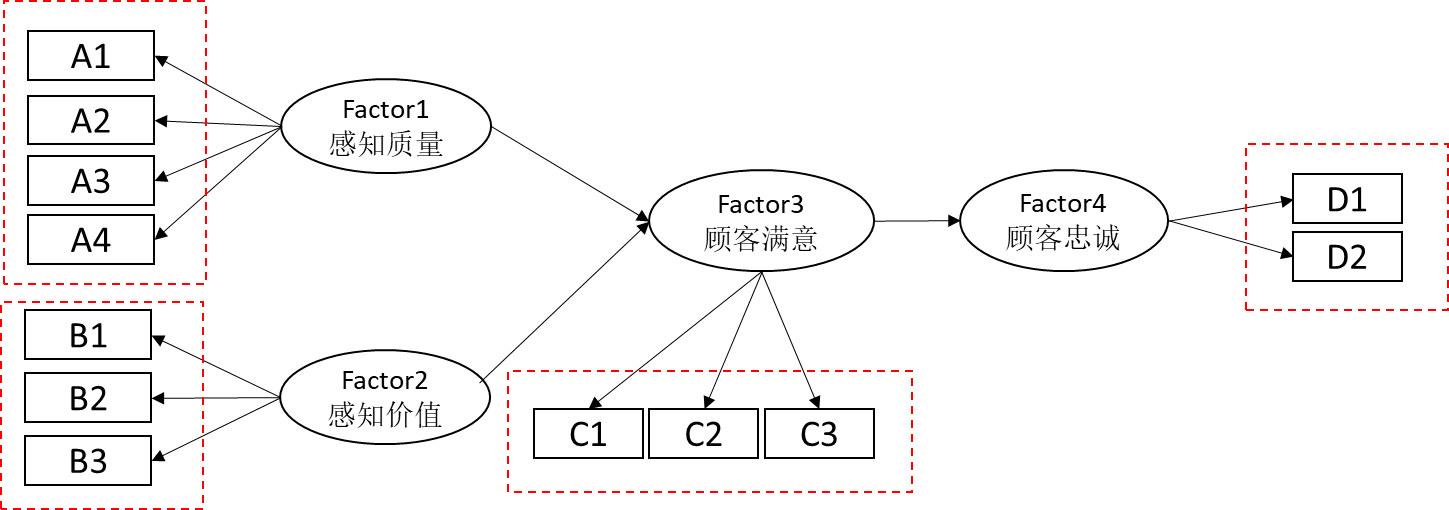
结构方程模型SEM是一种多元数据分析方法,其可用于研究多个潜变量之间的影响关系情况。结构方程模型共包括两部分结构,分别是测量关系和影响关系。比如下面这个结构方程模型,其包括四个潜变量,分别是Factor1感知质量、Factor2感知价值、Factor3顾客满意和Factor4顾客忠诚。
从测量关系来看:Factor1感知质量由A1~A4共4项测量;Factor2感知价值由B1~B3共3项测量;Factor3顾客满意由C1~C3共3项测量;Factor4顾客忠诚由D1~D2共2项测量。
从影响关系来看:Factor1和Factor2对于Factor3产生影响关系;Factor3对Factor4产生影响关系。
类似上述,如果研究中包括测量关系和影响关系时,此类研究均可称作结构方程模型。当然研究者的重心在于研究影响关系,并且进行假设验证等;测量关系并不在重点关注范围,但是测量关系的质量会对模型拟合情况产生很大的影响,因此研究者需要首先保证测量关系的质量情况。
-
特别提示
-
结构方程模型SEM包括测量关系和影响关系;如果仅包括影响关系,此时称作路径分析(Path analysis,有时也称通径分析)。
-
结构方程模型SEM对于测量关系和影响关系均有很高的要求;尤其是对于测量关系,因此研究前一定需要先保障测量关系有着高质量,通常需要进行探索性因子分析和验证性因子分析,均保证测量关系无误之后,再进行结构方程模型构建。
-
由于结构方程模型SEM对于样本量要求较高(通常200以上),以及测量关系,影响关系均有着很高的要求。因此有时会出现无论如何,结构方程模型SEM拟合效果均不理想,此时建议可将模型简化折分,也或者使用路径分析进行研究,如果路径分析也不理想,最终可考虑使用线性回归分析进行研究。
-
结构方程模型SEM案例
-
1、背景
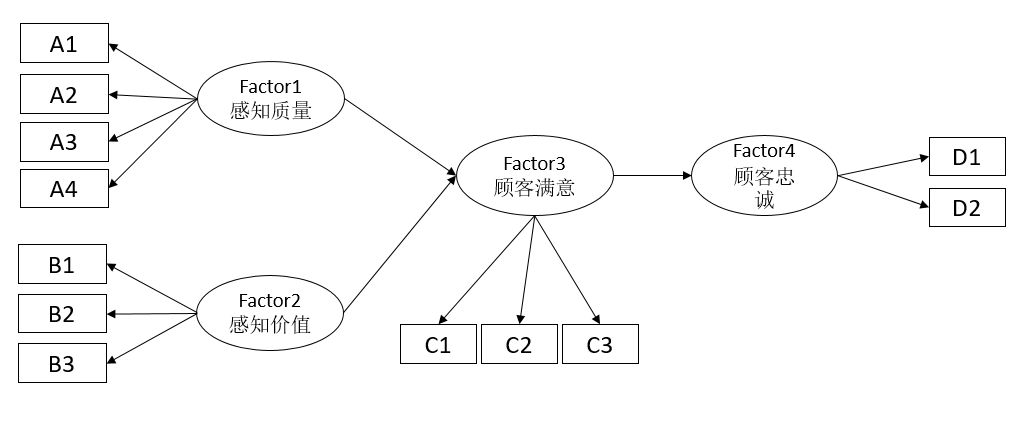
当前有一项研究,共收集样本为201份。并且建立预期模型如下,即研究Factor1和Factor2对于Factor3的影响关系;Factor3对Factor4的影响关系。预期模型如下图所示:
-
2、理论
结构方程模型对于数据质量,包括样本量,测量关系和影响关系均有着很高的要求;如果数据质量稍低则会导致拟合效果不佳,拟合指标不达标,因此SPSSAU提出以下结构方程模型分析流程,以保障高质量的结构方程模型拟合效果。如下图:
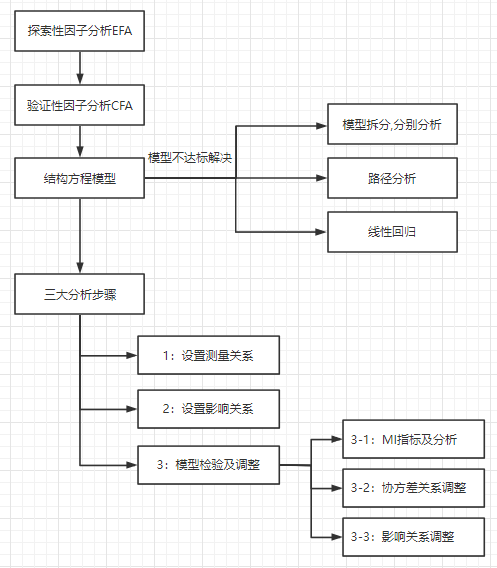
首先,如果想进行结构方程模型SEM分析,SPSSAU建议有效样本量需要在200份以上。同时在正式分析之前,需要保障测量关系具有良好的质量,通过探索性因子分析和验证性因子分析,共两步分析后,以保测量关系的高质量。
在确认好测量关系的高质量之后,接着正式进行结构方程模型构建。分别在SPSSAU平台上,设置好测量关系,影响关系后进行分析。如果对模型进行检验时有发现拟合效果不佳时,可考虑结合MI指标情况进行模型调整,此时有两种调整模型的办法,分别是和‘协方差关系调整’和‘影响关系调整’。
‘协方差关系调整’一般包括2种情况,第1种是指结合MI指标值情况,在原有模型基础上加入‘测量项’之间的协方差关系,此种调整的目的是在于调整‘测量关系结构’。第2种情况是建立factor与factor之间(也或者二阶Scale与Scale/factor)之间的‘协方差相关关系’。
‘影响关系调整’需要结合专业知识和MI指标进行调整,即重新在模型中加入影响关系,此种调整的目的是在于调整‘影响关系结构’。
如果模型无论如何拟合效果均不好,可有三种解决办法,第一种处理是将结构方程模型进行拆分成多个小模型分别进行分析;模型越复杂拟合要求越高,因此将模型的复杂度减低可有效提高拟合效果;第二种处理是改为路径分析(即直接放弃掉测量关系进行多元模型构建,尤其是测量关系质量不佳时);第三种处理是使用线性回归这种复杂度最低的模型进行研究。
-
特别提示:
-
结构方程模型一般要求样本量在200以上,如果过少可能拟合效果较差;
-
结构方程模型SEM构建前需要保障好测量关系的质量,建议结构方程模型SEM分析之前先进行探索性因子分析和验证性因子分析,确保测量关系良好后再进行SEM分析;
-
结构方程模型的分析包括三个步骤,分别是测量关系设置,影响关系设置,以及模型检验及调整;
-
模型调整包括两种,第1种是结合输出MI指标调整协方差关系,即重新加入测量项与测量项之间的协方差关系。第2种是结合MI指标建议及专业知识后,重新调整模型即加入影响关系路径;
-
如果结构方程模型SEM无论如何拟合效果均不好时,可考虑简化模型、使用路径分析、或者线性回归等进行处理解决。
-
-
3、操作
从上述理论描述可知,结构方程模型可分为三个步骤,第一步是设置测量关系;第二步是设置影响关系;分别如下所示:
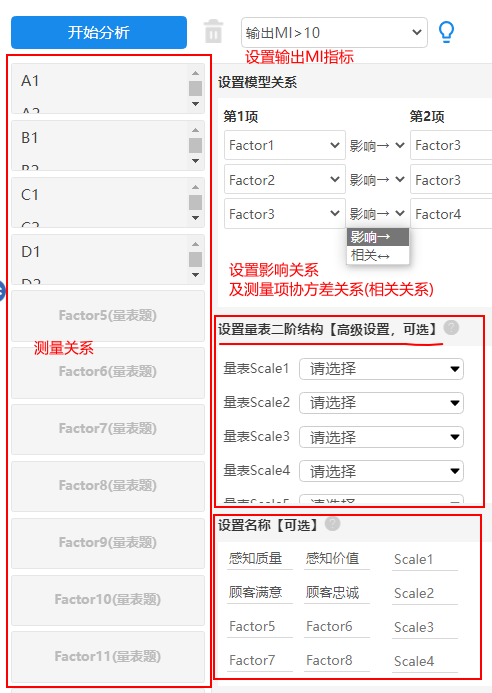
SPSSAU总共可设置12个潜变量,本例子中仅使用4个潜变量,因此分别将4个潜变量具体项拖拽到框中。并且SPSSAU默认潜变量的名称分别是Factor1,Factor2,Factor3和Factor4。并且对应的名称依次是感知质量、感知价值、顾客满意和顾客忠诚。
选择‘输出MI>10’的MI指标结果值,并且设置好4个factor之间的影响关系情况,分别是1->3,2->3,3->4。暂不设置‘测量项协方差关系(相关关系),一般情况下是模型修正调整时才会设置‘测量项协方差关系(相关关系)’。而且本次模型并没有二阶结构,因此不设置,具体二阶结构的内容可参阅本文档中的视频资料或其它文字说明。
-
特别提示
-
设置测量关系的潜变量,一定需要在 ‘影响关系’中出现;比如如果测量关系中有Factor5,但是影响关系中却没有出现Factor5,此时一定会出错。
-
-
4、SPSSAU输出结果
SPSSAU共输出7个表格,此7个表格的作用汇总如下:
名称 作用 模型回归系数汇总表格 潜变量之间的影响关系结果,以及测量关系结果,包括是否显著及回归系数等 模型拟合指标 模型拟合效果判断指标等 协方差关系-MI指标 用于辅助判断是否进行模型协方差相关关系调整的MI指标表格 影响关系- MI指标 用于辅助判断是否进行模型影响关系调整的MI指标表格 模型拟合度R方汇总表格 用于查看各项的R方值 协方差表格 用于查看协方差关系结果表格 残差项估计值 展示各项的残差项等,意义较小 具体7个表格的详细分析,在下面会有说明。
-
5、文字分析
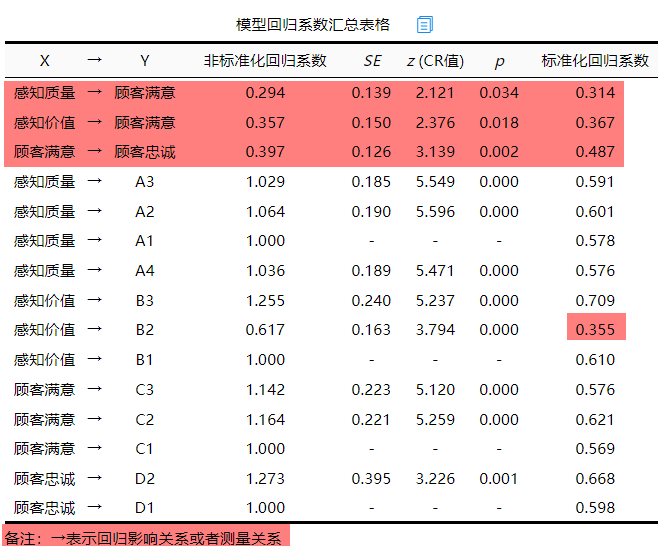
上表格展示潜变量的影响关系情况和测量关系情况,针对影响关系上,从上表可知:感知质量对于顾客满意产生0.05水平的显著影响,标准化路径系数值为0.314,意味着感知质量会对于顾客满意产生正向的影响关系。类似的,感知价值会对顾客满意产生显著的正向影响关系;同时顾客满意会对顾客忠诚产生显著的正向影响关系。
与此同时,‘模型回归系数汇总表格’还展示出所有的测量关系情况,在上表格中可直观查看,另外表格中出现‘-’时意味着该项为参照项因而不会输出。测量关系时第一项会被作为参照项,因此不会呈现P值等,比如A1被作为感知质量潜变量测量时的参照项,因此其对应的CR值,SE值和P值均为空,类似还有B1,C1和D1共3项。
上表格展示测量关系情况,如果测量关系良好,通常来说,标准化载荷系数值基本上均会大于0.6。上表格中B2的标准化载荷系数值为0.355比较低,如果发现模型拟合效果不好时,可考虑对其进行删除再尝试进行分析。(如果在SEM前进行过探索性因子分析和验证性因子分析,其实应该已经发现B2可能需要进行删除处理)。
上表格仅展示出测量关系时对应的系数值,以及辅助判断某项是否应该被删除处理掉,其并没有其它的意义了。当然上述结果需要在模型拟合效果良好的前提下才能使用,模型拟合效果需要通过‘模型拟合指标’表格进行分析。
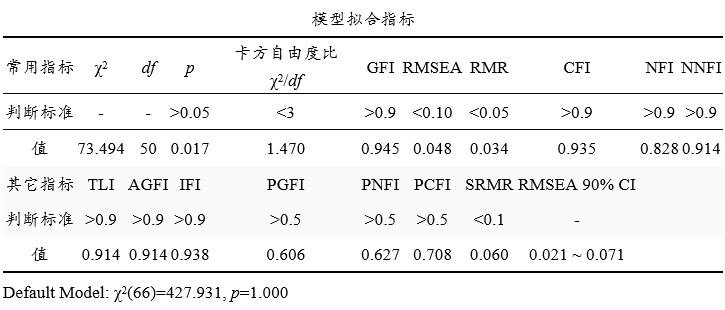
上表格展示模型拟合效果情况。模型拟合指标有很多很多,SPSSAU仅全部列出而已,很少有模型可以让所有拟合指标均达标,但使用最多的拟合指标建议需要在可接受范围内才可以,使用最多的拟合指标整理如下表:
最常使用拟合指标 标准 卡方自由度比 严格是小于3,不严格是小于5(甚至8) GFI 通常需要大于0.9,SPSSAU认为接受0.9基本可接受 RMSEA 严格是小于0.05,不严格是小于0.1 RMR 严格是小于0.05,不严格是小于0.1 CFI 通常需要大于0.9,SPSSAU认为接受0.9基本可接受 NFI 通常需要大于0.9,SPSSAU认为接受0.9基本可接受 AGFI 通常需要大于0.9,SPSSAU认为接受0.9基本可接受 结构方程模型SEM的拟合指标有很多,但并没有固定要求使用哪一些指标。多数研究仅会使用其中几个指标进行报告呈现。建议用户以相关研究文献参考作为最终标准。
本次研究时,卡方自由度比值为1.47,小于3,意味着模型拟合效果良好。同时RMSEA值为0.048小于0.05,RMR值为0.034小于0.05,同时GFI,CFI,AGFI值均大于0.9,NFI值为0.828小于0.9,但是接近于0.9,并且其余指标均在标准范围内,因此说明模型构建良好,模型结果可靠。

上表格展示协方差关系MI指标结果,而且本次参数设置为MI>10才会输出。如果模型拟合指标不好,可考虑需要建立B1与D1之间的协方差相关关系后再次分析。

上表格展示‘影响关系MI指标’,比如上表格中显示,本次参数设置为MI>10才会输出,结果均没有数据,意味着影响关系时MI指标均大于10,当然研究者可以重新设定MI>3这一标准输出MI指标数据,但是通常情况下MI值仅为个位数时其实已经较小。如果有出现MI值很大(比如大于20),此时可能需要对模型重新建立影响关系。
最终是否应该重新将上表格中建立的影响关系,加入到模型中(即重新建立模型);应该结合两点进行考虑。1是专业知识上是否允许;2是结合MI指标值及模型对比变化情况;如果专业上不允许即使MI值很大也不能修正模型,不能为了模型达标而随意调整模型。上表格没有数据结果即MI值全部均小于10,模型不需要进行调整(进行调整也不会让模型变得更好),因此当前模型即为最终模型结果。
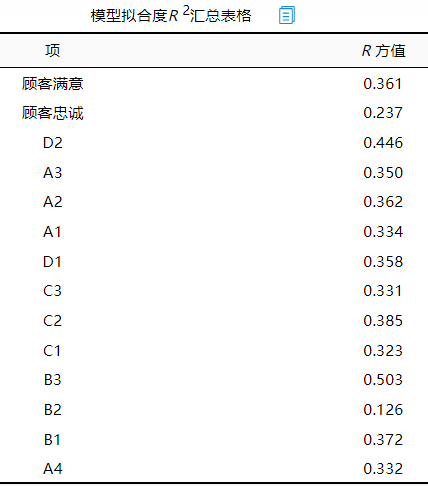
上表格展示拟合度R方值结果,该指标意义在于被影响的项即Y,它被影响项X的解释力度情况。测量项也会有R方值,但其无实际分析意义。
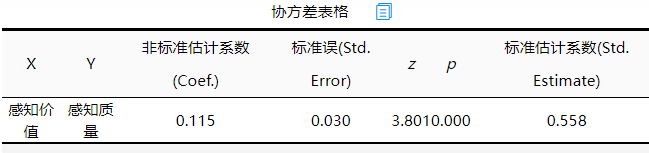
上表格展示协方差关系,即相关关系的意思。此种关系的出现有两种情况。第1种是SPSSAU自动建立的,上表格中显示感知价值和感知质量之间的协方差关系即相关关系系数为0.558(此关系是SPSSAU自动建立)。第2种是如果说研究者进行过‘模型协方差相关关系构建’,此时也会出现在上表格中。
上表格中感知价值和感知质量这两个外生变量,SPSSAU会自动识别出外生变量,并且自动建立起所有外生变量之间的协方差关系,通常其意义很小,原因在于研究的重心不在于协方差相关关系,而在于影响关系。只是出于模型建立的必要性(或者模型协方差关系修正),因此SPSSAU自动进行了建立;
完成上述表格之后,可将最终各结果系数整理汇总在一个图里面,便于展示结果,建立用户在PPT中进行绘图即可,类型如下图:
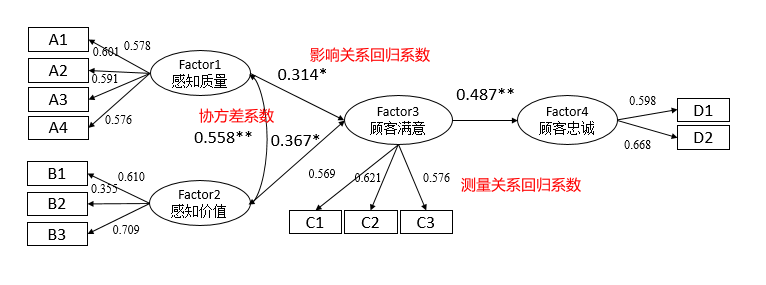
上图为手工PPT绘制,图中展示了‘测量关系和‘影响关系’(模型回归系数汇总表格 中的 标准化回归系数,并手工加入*号表示显著性)和协方差关系(协方差关系表格 中的标准化估计系数)。
-
特别提示
-
‘测量关系’时,箭头需要从潜变量指向测量项;‘影响关系’时,箭头从自变量X到因变量Y;协方差相关关系时,简单为双向。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
结构方程模型SEM包括测量关系和影响关系;如果仅包括影响关系,此时称作路径分析(Path analysis,有时也称通径分析)。
-
结构方程模型一般要求样本量在200以上,如果过少可能拟合效果较差;
-
结构方程模型SEM构建前需要保障好测量关系的质量,建议结构方程模型SEM分析之前先进行探索性因子分析和验证性因子分析,确保测量关系良好后再进行SEM分析;
-
结构方程模型的分析包括三个步骤,分别是测量关系设置,影响关系设置,以及模型检验及调整;
-
模型调整包括两种,分别是和‘协方差关系调整’和‘影响关系调整’。‘协方差关系调整’一般包括2种情况,第1种是指结合MI指标值情况,在原有模型基础上加入‘测量项’之间的协方差关系,此种调整的目的是在于调整‘测量关系结构’。第2种情况是建立factor与factor之间(也或者二阶Scale与Scale/factor)之间的‘协方差相关关系’。‘影响关系调整’需要结合专业知识和MI指标进行调整,即重新在模型中加入影响关系,此种调整的目的是在于调整‘影响关系结构’。
-
如果结构方程模型SEM无论如何拟合效果均不好时,可考虑简化模型、使用路径分析、或者线性回归等进行处理解决。
-
疑难解惑
-
提示‘数据质量异常’?
-
当提示“数据质量异常”时,可能有以下原因所致:
-
第一:如果样本量过小(比如仅几个样本),有可能模型无法拟合;
-
第二:研究关系中出现因果关系研究(比如X影响Y,同时Y影响X),此时有可能出现“数据质量异常”;
-
第三:模型MI调整值设置,如果模型中分析项(显变量)非常多时,按MI指标进行调整时,可能出现自动建立的协方差关系非常多,导致模型无法拟合,建议此时不进行MI指标调整,或者按较低标准设置即可;
-
第四:设置了二阶结构,但是关系里面没有出现该二阶Scale;也或者某factor已经在二阶结构中设置好,但却又出现在关系里面;也或者已经设置好factor对应的题,但在二阶结构或者关系中没有出现;
-
Factor,Scale分别是什么意思?
-
在结构方程模型中,涉及两个名词,分别是“显变量”和“潜变量”。“显变量”指具体有数据的分析项,即拖拽到Factor框中的具体项;“潜变量”指没有实际数据,但可以由“显变量”表示的变量,Factor和Scale均为“潜变量”。
-
比如综合满意度由3个维度表示(分别是价格满意度、服务满意度和质量满意度);价格满意度、服务满意度和质量满意度分别由5个具体题表示。那么总共15个题就是具体项即“显变量”;而3个维度也即3个Factor是潜变量;综合满意度由3个Factor表示,也即满意度为二阶Factor,也称Scale,它也是潜变量。一旦设置好测量结构关系,比如例子中最终设置了Scale,那么影响关系时,则只能出现Scale,而不能再具体其下属的Factor。
-
SPSSAU默认最多可设置12个Factor,5个scale。并且默认名字分别为Factor1,Factor2..直至Factor12。Scale1,Scale2..直至Scale5。
-
SPSSAU结构方程模型中如果输出MI值和如何使用它?
-
如果希望SPSSAU输出MI指标值,可在开始分析按钮右侧下拉选择输出MI值,比如‘输出MI>10’,其意义是将MI值大于10的全部输出(通常情况下MI值非常多,但一般只有较大的值才有参考意义)。在输出之后,可将MI值非常大的两两项之间建立‘协方差相关关系’(即相关关系,在‘设置模型关系’处进行设置),用于修正模型。MI值的修正通常会让卡方自由度值得到减少,其它指标一般不应该有太大的变化,不能过多的依赖于MI值进行模型修改。
-
提示‘数据质量异常’如何解决?
-
出现此种情况,建议按以下步骤进行检查并解决。
-
第一:相关性过低。同一个因子里面的项应该有很强的相关性才正常。因而建议把同一个因子里面的项做相关分析,如果发现某两项之间的相关性过弱(比如相关系数小于0.2),把其中一项从模型中移除出去,重复进行检查即可;
-
第二:样本量过低,比如总共有5个因子共计20个分析项,但分析样本量仅50个,这会导致模型无法收敛因而最终无法拟合。
-
结构方程模型中Scale(量表二阶结构)是什么意思?
-
Scale是量表的意思,比如一个Scale对应着3个因子,每个因子对应着具体几个量表题项。比如下图中的结构,Scale对应着3个Factor,每个Factor对应着一些题项。Scale即为二阶结构,相对模型会比较复杂时才会使用。
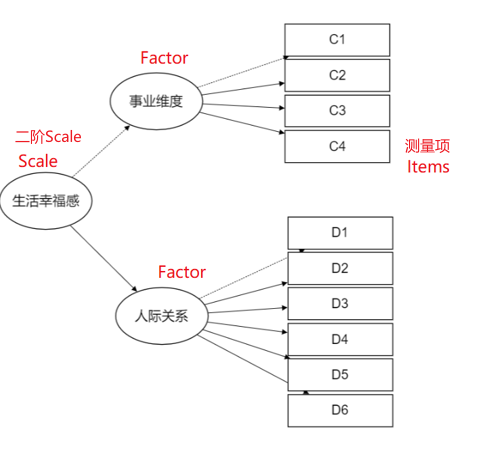
-
拟合度R 方值是什么意思?
-
R 方值是指模型拟合情况,X对于Y产生影响时,X对于Y的解释力度情况,比如为0.2,则说明X对于Y有20%的解释力度。每个Y都会产生对应的R 方值。通常以研究是否有影响作为研究目的,因此此指标的意义相对较小,关注也较少。
-
残差值估计值有什么作用?
-
该指标值通常无实际意义,只是模型拟合后产生的残差值而已。
-
结构方程模型使用的估计方法是?
-
SPSSAU默认使用最大似然法ML进行模型估计。
-
模型拟合度里面自由度为0?
-
模型拟合度出现自由度为0是正常现象,并且此时无法计算得到卡方值,卡方自由度值等,此时直接不关注对应的指标即可。出现自由度为0的原因通常是模型过于简单,或者模型过于‘饱和’,可能是非递归模型所致(比如A影响B,B影响C,C影响A)。
-
标准化载荷系数或标准化估计系数值大于1?
-
如果标准化系数值大于1,通常是由于出现共线性问题所致;建议可通过相关分析查看相关系数,如果某具体项之间的相关系数值非常高,可考虑移除该项;如果共线性不严重,通常并不需要移除。
-
图里面的虚线代表什么意思?
-
SPSSAU默认以放置顺序的第一项作为参考项,图里面的虚线标识出该项为参考项。参考项的非标准载荷系数值一定为1,而且不会有标准误值等。
-
残差值画图?
-
残差值无实际意义,SPSSAU的模型图里面默认没有提供残差值,但输出表格里面有。如果需要可自己手工作图处理。
-
分析框只能放20项?
-
在进行结构方程模型分析时,每个因子(维度)最多可放置20项。正常情况下,同一个因子(维度)正常情况下只会对应3~7项,如果超出10项,建议检查是否进行了正确的分析。
-
模型自动构建说明?
-
相对于传统软件进行结构方程模型构建,SPSSAU自动进行一些处理,便于简化操作。分别如下:第1是自动建立残差;第2是在结构方程模型构建时会将第1项的方差设置为1;第3是外生变量之间会自动建立协方差关系。第1点和第2点是基本默认性操作,正常的模型构建均应该如此;关于第3点,可通过结果中的“协方差关系表格”查看SPSSAU自动构建的关系。
-
结构方程模型拟合指标不好如何调整?
-
如果结构方程模型出现拟合指标不好,大方面的原因可能有两个,分别是模型的‘测量结构’有问题,也或者‘影响关系结构’有问题。建议按以下7种方式进行调整或分析。
-
第1是先进行探索性因子分析,再进行验证性因子分析,保障验证性因子分析等结果良好后再做结构方程模型,此种分析思路在于保障‘测量结构’稳定。此种思路最为重要,因为结构方程模型中包括大量的‘测量结构’,一旦‘测量结构’不合理,无论如何拟合指标均不好;
-
第2是将"模型回归系数汇总表格"结果中出现不显著的关系项,从模型中移除出去。此处理在于优化‘测量结构’和‘影响关系结构’;
-
第3是结合‘影响关系- MI指标’表格,将该表格中MI值较大项加入模型中,此种处理在于优化‘影响关系结构’;
-
第4是进行MI指标调整,比如输出MI>10的数据结果,然后将结果中MI值过高的两两测量项建立协方差相关关系,然后再次进行分析,此种做法在于优化'测量结构',如果模型拟合指标非常糟糕,通常此种处理并不生效,此种处理通常只会降低卡方自由度值,对其它指标帮助非常小;
-
第5是简化模型,从专业角度出发,将模型进行分拆成多个,越简化的模型越容易拟合成功,此种处理在于优化‘影响关系结构’和‘测量结构’;
-
第6是改用路径分析模型,路径分析模型是不带‘测量结构’的结构方程模型,直接不考虑‘测量结构’,此种处理在于优化‘测量结构’,此种处理通常会生效;
-
第7种是改用线性回归模型,线性回归也不用考虑测量结构,而且模型变的更加简单,此种处理在于优化‘测量结构’和‘影响关系结构’,此种处理通常会生效。
-
分析项超过60个不进行MI指标输出和自动按MI指标建模什么意思?
-
如果说分析项(显变量)的个数大于60个,SPSSAU默认不会输出MI指标值,并且如果用户要求进行按MI指标调整模型,SPSSAU也不会进行模型调整。
-
z 值和临界值或t 值的意义?
-
结构方程模型时,SPSSAU输出z 值,该值与AMOS软件等的临界值CR或t 值意义完全一致。
-
结构方程模型如何输出MI指标值?
-
进行结构方程模型时,可在开始分析按钮右侧“MI指标输出”下拉,选择输出MI指标值。如果需要结合MI指标情况进行模型调整,那么可在‘设置模型关系’时设置具体测量项之间的相关关系(协方差关系)即可。MI值越大意味着可减少的卡方值越多,结合该指标进行模型调整时,一般会对卡方自由度值有着较大的帮助。
-
结构方程模型每个框最多可放多少项?
-
结构方程模型时,第个因子框中放置的是其对应的测量项,正常情况下一个因子会对应3~7个测量项。SPSSAU默认最多支持1个因子框中放置20个测量项。
-
测量项需要在因子框中出现!
-
结构方程模型设置时,如果需要建立测量项之间的协方差相关关系,那么测量项一定需要隶属于某个因子(即在某因子框中出现过才可以)。
-
有设置某Scale,则关系中应出现该Scale!
-
结构方程模型设置时,如果设置过二阶量表Scale,那么模型关系中一定需要使用它(否则设置二阶量表就没有意义)。
-
设置过某Factor,则关系/Scale中应出现该Factor!
-
结构方程模型设置时,如果设置过某个Factor,那么Factor需要出现在模型关系中(当然Factor可能隶属于某个Scale,那么此时模型关系中就应该以对应的Scale为准,模型关系中也不能再出现该Factor)。
-
没有设置某Scale,则关系中不能出现该Scale!
-
结构方程模型设置时,如果说没有设置过某二阶结构Scale,那么模型中就不能出现该Scale。
-
没有设置某Factor,则关系/Scale中不能出现该Factor!
-
结构方程模型设置时,如果说没有设置过某个Factor,那么就不能在模型关系(也或者二阶结构Scale中出现该Factor)。
-
一个Factor不能隶属于多个Scale!
-
一个Factor只能隶属于1个二阶结构Scale,不能隶属于多个Scale。
-
1个Scale需要对应至少2个Factor!
-
1个Scale至少需要对应2个factor,否则的话就不需要设置Scale,而是直接以Factor为准进行分析即可。
-
关系设置时,测量项只能与测量项建立协方差关系!
-
如果想建立测量项之间的关系,分析上只能建立协方差关系,通常测量项之间协方差关系的设置依据是结合MI指标值进行。
-
SPSSSAU结构方程模型没有出现测量关系表格?
-
SPSSAU21.0版本起,结构方程模型中的测量关系会放到回归关系中(即‘模型回归系数汇总表格’中),事实上测量关系从数学角度就是一种回归关系,研究者自行知晓对应的测量关系情况即可。
-
路径系数,回归系数是一个意思吗?
-
SPSSAU进行结构方程模型或者路径分析时,会提供路径系数指标,其与回归系数的意义一致,可直接理解为回归系数即可。
-
模型是由系统自动绘制,通常情况下建议先对标题进行简化后再进行分析。比如标题简化为A1,A2,A3,B1,B2,B3,满意度1,满意度2,满意度3等。可通过SPSSAU数据处理->标题处理,批量修改标题名称。
标题过长模型不美观如何图形?
-
中介作用的检验方式通常包括‘逐步检验法’和‘bootstrap法’。如果是使用‘逐步检验法’,可使用线性回归或分层回归等完成,如果是使用bootstrap法,可使用SPSSAU中介作用方法完成。至于结构方程模型进行中介作用,SPSSAU暂没有提供bootstrap法,可考虑使用‘逐步检验法’原理进行结构方程模型,进而进行中介作用检验。具体‘逐步检验法’的原理说明可点击查看。
SPSSAU的结构方程模型进行调节作用?
-
调节作用检验的原理是交互项显著性,建议使用SPSSAU调节作用、或者分层回归进行分析。具体原理可点击查看。当前SPSSAU结构方程模型无法进行调节作用分析,可考虑将潜变量生成平均值得到显变量后再进行即可。
SPSSAU的结构方程模型如何进行中介作用?
-
在某些特殊情况下,此时模型极其糟糕(特征上会出现比如很多影响关系均明显的不显著,也或者拟合指标基本不达标)时,此时模型计算收敛性不稳定可能出现同样的操作结果不同(且差异很大),建议此时检查模型是否适合(因为此种情况下模型糟糕无法使用),以及处理上通常是移除非常不显著的关系路径重新分析,让模型稍正常即可。
结构方程模型出现随机性结果?
-
如果进行SEM模型分析,SPSSAU默认会对外生变量之间建立协方差关系,此方式与R软件保持一致,此功能暂无法取消。
SPSSAU进行结构方程模型时会自动建议协方差关系?
-
SPSSAU进行SEM模型分析绘制模型图时,模型图中默认没有提供残差项,研究者可下载模型图手工进行绘制或者忽略(默认情况下残差项从分析视角上无实际意义)。
