问卷研究中,如果涉及计算权重,通常有以下几种做法,分别是AHP层次法、优序图法、熵值法、因子分析法(探索性因子和验证性因子分析)。在问卷研究》权重这个按钮里面,SPSSAU提供两种方法,分别是AHP层次法和优序图法。汇总说明如下:
| 权重计算方法 | 关键点 | 位置 |
| AHP层次法 | 利用相对重要性进行权重计算 | 问卷研究》权重 综合评价》AHP层次分析法 |
| 优序图法 | 利用相对重要性进行权重计算 | 问卷研究》权重 |
| 熵值法 | 利用熵值信息进行权重计算 | 综合评价》熵值法 |
| 探索性因子分析法 | 利用浓缩因子的方差解释率计算 | 进阶方法》因子分析 |
| 验证性因子分析法 | 利用载荷系数值计算 | 问卷研究》验证性因子分析 |
| 其它 | 综合评价板块 |
如果问卷研究中涉及到重要性打分题,也或者排序题,也或者量表题,此类题的特点是分值越高代表越重要,或者越认可。那么可以理解为重要性越高,权重也会越高。因此可以利用此信息进行权重计算,分别使用到AHP层次分析法和优序图法,此两种研究方法均是利用相对重要性进行权重计算。
AHP层次分析法本身是一种专家打分赋权法,即通过专家打分去描述相对重要性,进而计算得到权重。SPSSAU默认对分析项进行平均值计算,并且利用平均值信息得到相对重要性大小,构建出AHP层次分析法需要的判断矩阵,从而计算得到权重。如果是使用AHP层次分析法,用户也可以自己构建判断矩阵,然后自己手工录入数据进行AHP层次分析法计算,具体可参考此页面详细说明: https://www.spssau.com/helps/weights/ahp.html
类似地,优序图法也是利用相对重要性原理进行权重计算,SPSSAU默认对分析项计算出平均值,并且结合平均值的相对大小构建出优序图权重计算表,进而计算得到权重。
-
特别提示:
-
问卷研究》权重这里的AHP层次分析法,事实上是SPSSAU自动进行了判断矩阵的构建,从而计算得到权重,研究人员也可以使用综合评价》AHP层次分析法,自己输入判断矩阵,进而计算权重,效果是完全一样的。具体关于AHP层次分析法的原理和详细说明,请参考此页面: https://www.spssau.com/helps/weights/ahp.html
问卷权重分析案例
-
1、背景
当前有一项关于网购在乎因素的权重研究,涉及网购在乎因素共为9项,分别是指标1,指标2到指标9。然后使用问卷形式让30名专家对此9个指标的重要性进行打分。利用专家打分进行权重计算,得到此9个指标的权重值。

-
2、理论
AHP层次分析法和优序图法,此两种方法均是利用数据的相对重要性,进而构建出权重计算矩阵进行计算。因此意味着数字越大,其相对重要性会越高,比如本案例中共有9个指标,SPSSAU会首先计算出此9个指标的平均值,然后利用平均值进行矩阵的构建。本次案例中9个指标的平均值得分如下:
名称 指标1
重要性指标2
重要性指标3
重要性指标4
重要性指标5
重要性指标6
重要性指标7
重要性指标8
重要性指标9
重要性平均值 4.100 3.967 3.867 4.300 3.767 4.033 4.133 4.000 4.133 如果是使用AHP层次分析法,SPSSAU自动构建出相对重要性判断矩阵如下。

上表格为AHP层次分析法时SPSSAU自动构建的判断矩阵,比如表格中数字0.967表示指标2相对于指标1的重要性大小,该值=指标2的平均值/指标1的平均值,即0.967=3.967/4.100。接着再根据此判断矩阵进行AHP层次分析法的相关计算,具体关于AHP层次分析法的原理和详细说明,请参考此页面: https://www.spssau.com/helps/weights/ahp.html
如果是使用优序图法,SPSSAU自动构建出优序图权重计算表如下:
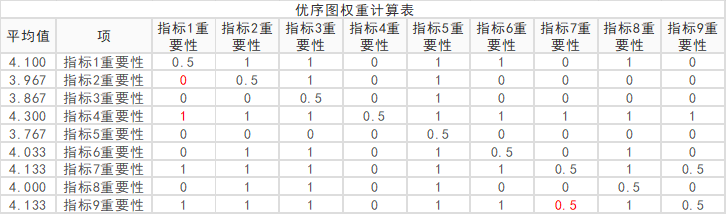
上表格中数字0表示相对不重要,数字1表示相对更重要,数字0.5表示一样重要。比如指标2的平均值为3.967,指标1的平均值是4.1,因此指标2不如指标1重要;指标4的平均值为4.3,重要性高于指标1。也或者指标7和指标9的平均得发均为4.133分,因此它们的重要性一样,记为0.5。
-
3、操作
本例子以优序图法进行讲解, 操作截图如下:
-
4、SPSSAU输出结果
使用优序图法进行权重计算时,SPSSAU共输出两个表格,分别是优序图权重计算表和优序图权重计算结果表格。
-
5、文字分析

本次研究共收集30个专家关于网购在乎因素9个指标的重要性打,分值越高代表重要性越高,同时利用9个指标的平均重要性得分值(平均值),构建出优序图权重计算表格。表格中数字0表示表示指标A相对指标B不重要(即指标A的平均值小于指标B的平均值),数字1表示指标A相对指标B更重要,数字0.5表示指标A和指标B一样重要。
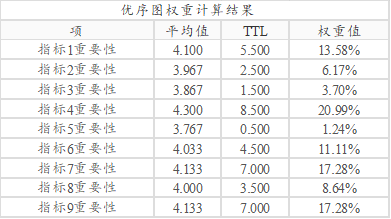
构建完成优序图权重计算表格之后,针对每行进行加和,得到TTL值,比如指标1时TTL值为5.5=0.5+1+1+0+1+1+0+1+0。类似的得到全部指标的TTL值,然后利用TTL值进行归一化处理,最终计算得到9个指标的权重值。
从上表格可以看到,指标4的重要性最高,权重占比是20.99%,其次是指标7和指标9,占比均为17.28%。指标3的重要性最低,因此权重最低为3.70%。
-
6、剖析
涉及以下几个关键点,分别如下:
-
AHP层次法和优序图法都完全利用数字重要性大小进行权重计算,通常适用于专家打分;
-
如果是排序题,或者重要性打分题,均可考虑使用AHP层次分析法或优序图法完成权重计算。
-
AHP层次分析法时,通常情况下是自己构建判断矩阵然后计算。问卷研究》权重按钮里面的AHP层次分析法,其实质是SPSSAU自动进行判断矩阵后进行计算,便于研究人员快速完成研究。其实质上就是综合评价里面的AHP层次分析法。如果是自己手工录入判断矩阵进行AHP层次分析法计算,具体可参考此页面详细说明: https://www.spssau.com/helps/weights/ahp.html
-
疑难解惑
-
RI值与参考文献不一致?
-
平均随机一致性指标RI值通过随机值工程计算得到,本身就带有随机性,但此种随机性体现在数值上仅有非常细微的区别,并且是正常且正确的。SPSSAU使用的RI指标值参考文献如下:
-
洪志国, 李焱, 范植华, et al. Caculation on High-ranked R I of Analytic Hierarchy Process%层次分析法中高阶平均随机一致性指标(RI)的计算[J]. 计算机工程与应用, 038(12):45-47,150.
-
优序图法里面的TTL是什么?
-
TTL是指标得分值,该分值越大说明权重会越高,以及该分值进行归一化后即得到最终的权重值。
-
CI值为0?
-
CI值用于检验一致性,即数据之间是否存在逻辑性,如果使用问卷研究->权重计算AHP权重,系统自动进行平均值大小对比,不会有任何的逻辑问题,因此CI值为0。
-
权重计算出来为0?
-
SPSSAU问卷研究中的权重->AHP法计算时,首先会计算指标的平均值,利用平均值构建判断矩阵。如果说原始数据中出现负数则可能导致平均值有为负数或为0,这是不允许的。可通过描述分析查看数据是否有这一特征。如果确定原始数据中有异常值,可使用数据处理->异常值功能将异常值(小于等于0)设置成null后再分析即可。
-
优序图法、熵值法、AHP法如何选择?
-
如果是希望结合数字大小进行权重计算,比如数字越大即权重越大,此时可使用优序图法或AHP法,AHP法一般是专家打分时使用较多。如果是根据数字本身的熵值进行权重计算,则选择熵值法即可。
