均匀设计案例

• 1、理论

  均匀设计的原则是使试验点在试验空间内分布均匀，并且其通过计算试验点分布的（Discrepancy）来评估均匀性，其理论是基于数论方法和组合数学构建设计表。

  相对于正交设计，均匀设计更强调‘均匀分散性’，但其无‘整齐可比性’特点；关于‘均匀分散性’：其是指实验设计很均匀散开，可全面覆盖设计空间以避免偏差；关于‘整齐可比性’：其是指可有效地识别区分每个因子的效应，每个因子效应互不干扰（即在数学上称为‘正交性’即无相关性），正交设计具有‘均匀分散 整齐可比’的特点，但均匀设计无‘整齐可比’这一特点。

  但是相比全面试验或正交试验，均匀设计可大大减少试验次数，并且其对因子水平数没有严格限制，适用于各种类型因子，整体来看均匀设计时试验点在整个试验区域内分布均匀，而且可根据实际需要选择试验次数和因子数。均匀设计适用于多因子、多水平的复杂试验，也或者试验成本高、周期长的研究项目，以及如果因子间可能存在复杂非线性关系的情况时，此时也可使用均匀设计。除此之外，整理各类试验的优缺点对比如下表格：

  设计方法	实验次数	适用因子个数	说明
  全面试验（比如2水平析因）	n^k（n为水平个数，k为因子个数）	无限制	信息完整但试验量大，适用因子数和水平数均较少
  正交设计	固定	一般≤10	均匀分散、整齐可比，适用于各因子水平数相等或成倍数
  均匀设计	灵活选择	无严格限制	均匀分散，适用于多因子、多水平复杂试验
  响应面设计	中等	2~10个	可拟合二次模型，适用于参数优化、寻找最优点

  比如析因设计，其通常仅适用于因子个数很少的情况，因为通常其实验次数会随着因子个数及水平个数而明显上升；正交设计适用于10个内的因子情况；响应面设计也适用于2~10个因子时但响应面设计可偏向于分析角度，比如需要拟合二次模型，寻找最优点等；均匀设计适用于多因子且多水平的复杂试验场景，其对因子个数限制少且实验次数也非常灵活。

  关于均匀设计的算法实现，SPSSAU借助R语言的mixtox包完成。参考文献如下：

  Xiangwei Zhu. (2022). Mixtox. R package version 1.4.0. Available at: https://CRAN.R-project.org/package=mixtox.

• 2、操作

  SPSSAU平台中进行均匀设计时，仅需要设置因子个数和预期的试验次数即可，当然也可设置因子的名称，以及因子类型及其水平值信息等，如下图所示：

  

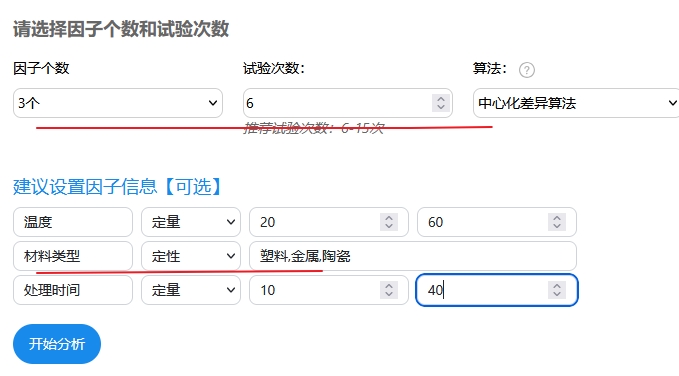
  关于因子信息设置，比如温度，其为定量数据并且介于20到60度之间，那最小值和最大值分别设置即可。比如材料类型这种因子，其是3个类别即定性数据，因而可如图所示，以逗号形式隔开各个水平值。处理时间最小为10分钟最大为40分钟，如图设置即可。

  关于均匀设计求解算法上，默认推荐使用中心化差异算法，其在大多数情况下能产生更均匀的设计，并且计算复杂度适中；SD2（对称差异）算法在某些特殊情况下可能表现更好计算时间可能较长。

  点击‘开始分析’后即得到均匀设计表格，如果有设置过‘因子信息’，SPSSAU会提供‘实际值’表格，其将因子名称及因子水平值等信息展示在表格中，例于实验研究人员参考和记录信息；试验方案编码表格为编码值表格，其里面的编码值是数理上的一个位置编号，用于控制试验均匀性和分布性保证试验点在设计空间中合理分布的数字。编码值和‘实际值’表格有着映射逻辑关系（如下述）。

  除此之外，默认SPSSAU会输出差异值（Discrepancy），该值表示试验点在试验空间中的分布均匀程度情况，该指标越小越好，可对比不同实验设计的优劣情况。

  

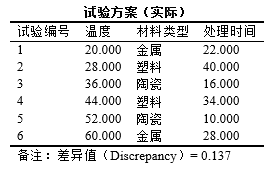
  上表格为实际实验使用时的表格，下表格为试验方案即编码值表格，二者的映射关系说明如下：

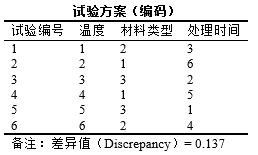
  项	映射关系
  定量数据	实际值 = 最小值 + (编码值-1) × (最大值-最小值)/(水平数-1) 其中：水平数为均匀设计编码表格后不同的数字个数。
  定性数据	编码表格中的1/2/3等表示该因子的对应水平值，比如下表格中2则会展示成塑料，2展示成金额，3展示成陶瓷

  针对定量数据，比如本例子中温度最小为20，最大为60，编码值为1时，则实际值=20+(1-1)*(60-20)/(6-1)=20，编码值为2时，则实际值=20+(2-1)*(60-20)/(6-1)=28。

  针对定性数据，比如本例子中的材料类型，其1/2/3等表示材料类型对应的3个水平值分别是塑料/金属/陶瓷。

  

• 3、剖析

  涉及以下几个关键点，分别如下：

  • 均匀设计时，实际值表格和编码值表格的区别？

  • 编码表格是均匀设计生成的原始试验方案，每一列代表一个因子，每一行代表一个试验点，编码表格中的数字是编码值，通常是整数，比如 1、2、3，其表示该因子在该试验点上取第几个水平。

  • 编码值不代表实际物理量，只是一个位置编号。用于控制试验的均匀性和分布性，确保试验点在设计空间中分布合理。实际值表格是将编码值转换成真实的物理量或工艺参数值，用于实际操作或实验，表格中的数字是真实的实验条件，比如温度、浓度、时间等，实际值表格是实验人员真正执行的试验方案。

  • 如果设置过因子信息，SPSSAU会自动映射编码值和实际值，输出实际值表格，但如果没有设置过因子信息，SPSSAU此时仅会输出编码值表格。

  • 均匀设计时，编码值的实际意义？

  • 编码值并不实际意义，编码值是试验设计中的“位置编号”，用于构造均匀分布的试验点，最终通过映射转换为实际的实验条件。当定性且设置水平值时，编码值的顺序就是水平值的顺序，如果定性但没有设置水平值时，编码值无实际意义。定量数据时，编码值也无实际意义。但编码值可通过映射关系映射成实际值，实际值具有意义。以及分析角度时可能使用到编码值，因为当定量数据时，编码值的具体大小无实际意义，但相对大小有意义；定性数据且有设置水平值时，编码值可表示各个不同的水平值。