统计分布图

• 1、理论

  SPSSAU提供七种常见分布的p 值计算或转换（统计量转换成p 值，或者p 值转换统计量），并且可视化呈现p 值。具体说明如下：

  • 正态分布(Normal Distribution)

  • z 值转p 值计算：根据标准化z 值和检验类型(单侧/双侧)计算对应的p 值

  • p 值转z 值计算：根据给定的p 值和检验类型反推对应的z 值

  • 应用场景：假设检验、置信区间计算、质量控制等

  • F分布(F Distribution)

  • F 值转p 值计算：根据F 统计量和两个自由度(df1, df2)计算p 值

  • p 值转F 值计算：根据p 值和两个自由度反推临界F 值

  • 应用场景：方差分析(ANOVA)、回归模型显著性检验等

  • t分布(t Distribution)

  • t 值转p 值计算：根据t 统计量、自由度和检验类型计算p 值

  • p 值转t 值计算：根据p 值、自由度和检验类型反推临界t 值

  • 应用场景：小样本假设检验、回归系数显著性检验等

  • 卡方分布(Chi-square Distribution)

  • 卡方值转p 值计算：根据卡方统计量和自由度计算p 值

  • p 值转卡方值计算：根据p 值和自由度反推临界卡方值

  • 应用场景：拟合优度检验、独立性检验、方差检验等

  • 二项分布(Binomial Distribution)

  • 成功次数转p 值计算：根据成功次数、试验次数和成功概率计算累积概率

  • p 值转成功次数计算：根据累积概率、试验次数和成功概率反推临界成功次数

  • 应用场景：质量检验、医学试验、市场调研等

  • 泊松分布(Poisson Distribution)

  • 事件次数转p 值计算：根据事件发生次数和平均发生率计算累积概率

  • p 值转事件次数计算：根据累积概率和平均发生率反推临界事件次数

  • 应用场景：稀有事件建模、排队论、可靠性分析等

  • 负二项分布(Negative Binomial Distribution)

  • 试验次数转p 值计算：根据试验次数、目标成功次数和成功概率计算累积概率

  • p 值转试验次数计算：根据累积概率、目标成功次数和成功概率反推临界试验次数

  • 应用场景：质量控制中的抽样检验、生物统计、保险理赔等

• 2、操作

  通过SPSSAU统计控制模块，可进入统计图，默认是正态分布图，下述：

  

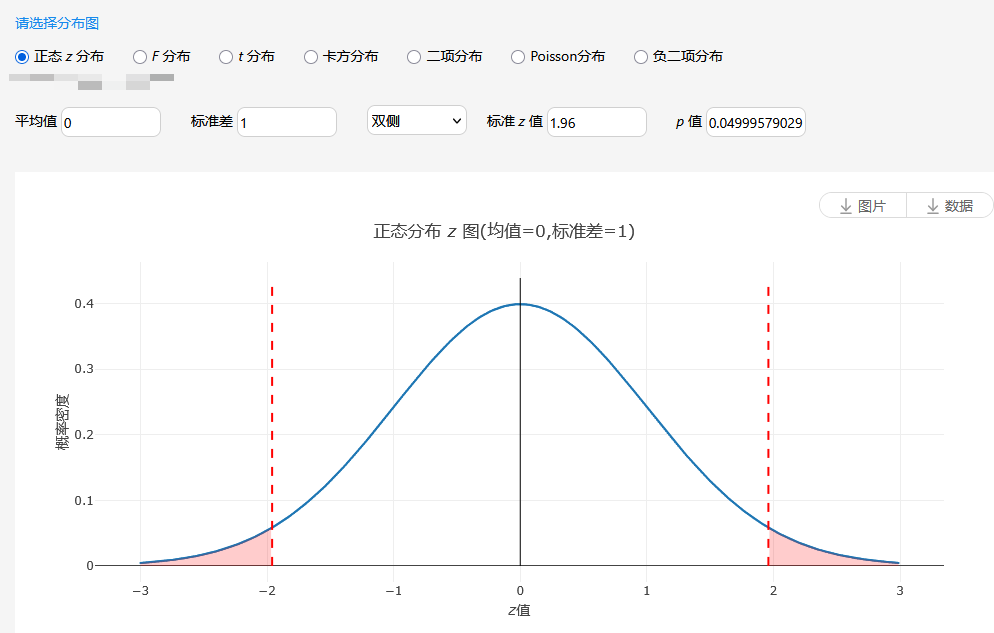
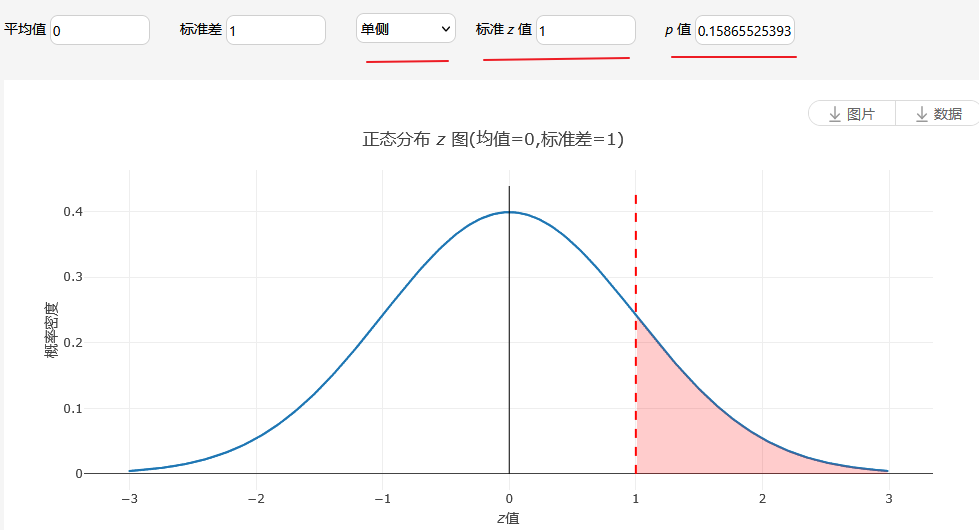
  图中展示正态分布图涉及的几项参数，包括平均值和标准差，当涉及到p 值计算时，其还需要设置双侧/单侧检验，以及结合标准化z 值，可计算得到p 值。比如上图中为‘双侧’，并且标准化z 值为1.96，那么图示中的左右两个红色部分加和即为p 值的可视化呈现。当然可以随意的改变标准化z 值，比如设置为1，并且为单侧，此时p 值为0.15865525393145707，如下图所示。

  

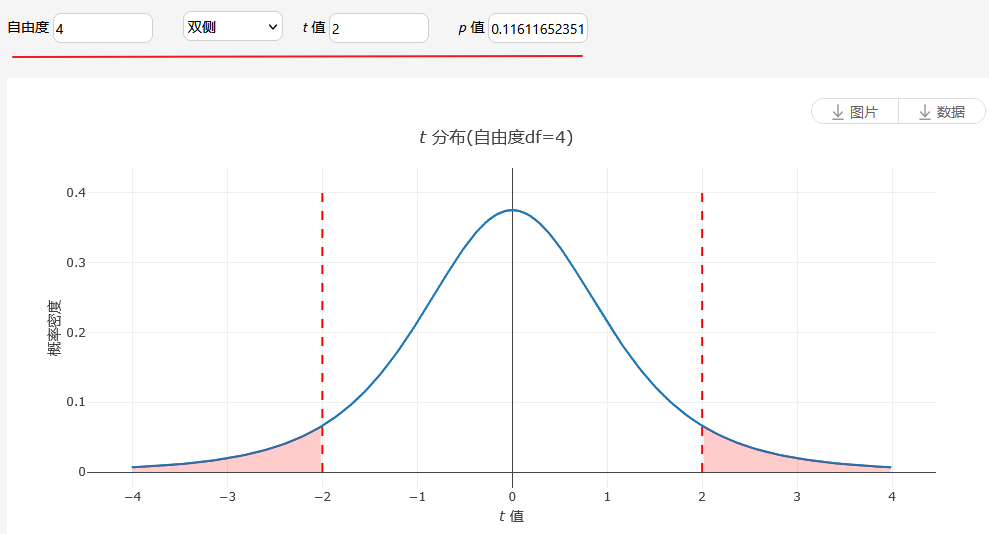
  类似地比如：t 分布时，结合自由度为4，双侧检验和t 值等于2时，可计算得到p 值为0.116116523516816，此处p 值的计算即为比如独立t 检验、单样本t 检验、配对t 检验，也或者线性回归系数的p 值检验数学原理。

  

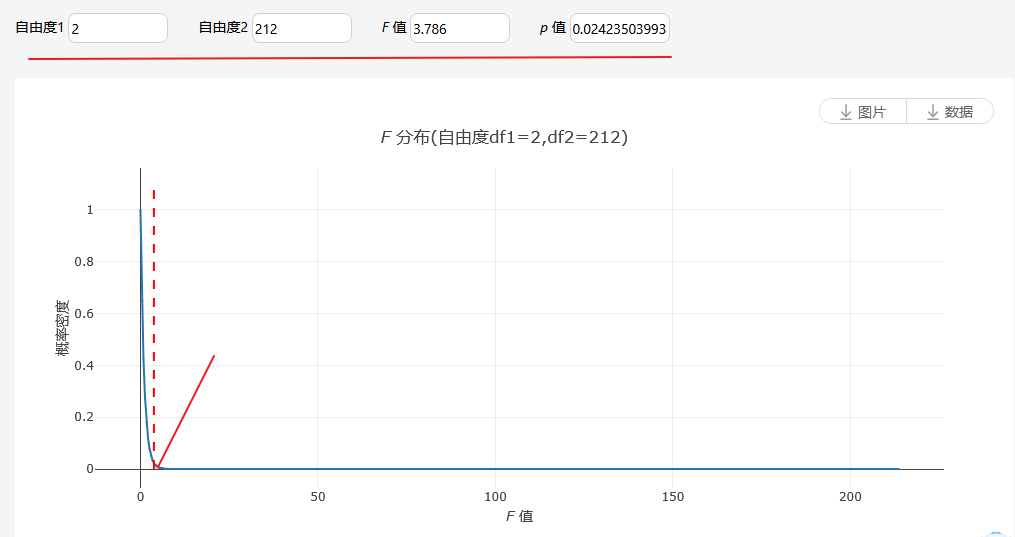
  类似地比如F 分布时，比如SPSSAU中有输出F 检验为比如‘F (2,212)=3.786,p =0.024’，则意味着两个自由度分别是2和212，F 值为2.786，计算出来p 值为0.024，如下图所示（大于虚线即3.786右侧的非常小部分面积即为p 值的可视化呈现）：

  

• 3、剖析

  涉及以下几个关键点，分别如下：

  • 正态分布时，标准化z 值和标准化p 值是什么意思？

  • SPSSAU统计分布图时，其提供标准化z 值和标准化p 值的自动计算，并且在统计图中可视化呈现p 值信息，其为标准正态分布函数作为前提，因此修改平均值或者标准差时，对应的该2项值并不会有任何变化。