响应面分析
-
案例数据下载 下载
响应面分析(Response Surface Methodology, RSM)是一种结合数学和统计学技术的优化方法,用于建立和分析影响因素(自变量)与响应值(因变量)之间关系的模型。通过构建近似函数关系,RSM可以帮助我们理解和优化复杂系统的行为,找到最优的操作条件。响应面分析通常是基于多元二次回归模型,通过设计实验收集数据,然后拟合回归方程来描述因素与响应之间的关系。模型形式通常为:
其中:Y 是响应变量,Xi是自变量(因素),β0, βi, βij, βii是回归系数,ε是误差项。首先,RSM需要考虑基本的主效应,即公式里面的Xi,与此同时,多数情况下,响应面分析需要考虑交互效应即模型里面的XiXj,但是否考虑二阶效应即Xi2,此处需要结合实际情况判断,并非必须项。
正常情况下,RSM是基于实验方案收集数据后进行分析,实验方案通常为中心复合设计(CCD)和Box-Behnken设计(BBD)等。RSM一般用于工艺参数优化,比如制药行业中药品本文优化;质量控制与改进,比如研究最小化缺陷率;产品设计与开发,比如新产品本文设计;相关实验研究,比如生物学实验条件优化等。
响应面分析案例
-
1、背景
当前某化工企业生产高分子聚合物的反应过程,其希望通过响应面分析方法优化反应条件(共5项因素),以获得最佳的‘产品纯度’,此处‘产品纯度’值为越大越好。前期其采用中心复合设计并且通过合理实验点安排,收集到不同因素水平组合下的‘产品纯度’数据。
-
2、理论
响应面是描述响应变量与一组输入因素之间关系的多维曲面。简单来讲,其就是研究因素与响应变量之间的数学关系表达。如果是最简单的主效应(完全不考虑交互效应和平方效应),那么其数学公式为:Y = β0 + β1X1 + β2X2 + ... + βkXk + ε。如果需要考虑交互效应和平方效应,那么其数学公式为:Y = β0 + ΣβiXi + ΣβijXiXj + ΣβiiXi2 + ε。其中,β0是常数项,βi是线性系数,βij是交互项系数,βii是二次项系数。
数学原理上,上述数学模型公式通过最小二乘法进行估计,并且得到回归方程,与此同时,还会进行方差分析等得到相关指标结果。
-
3、操作
响应面分析的数据通常来源于实验设计,比如BBD设计和CCD设计,并且需要在SPSSAU中设置相关的参数。本案例操作截图和参数设计等,说明分别如下:
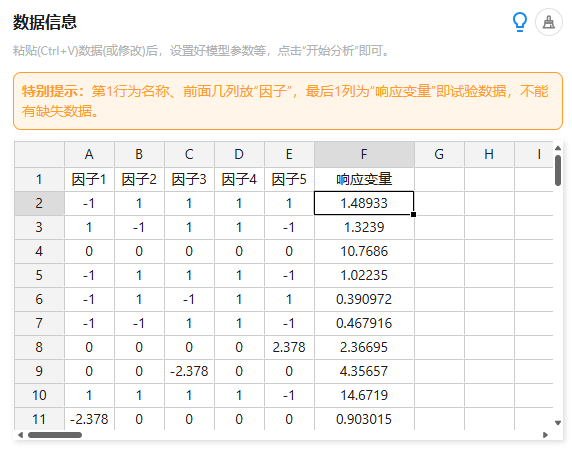
首先在编辑框中直接粘贴试验数据,需要注意的是:
-
特别提示:
-
第1行为名称、前面几列放“因子”,最后1列为“响应变量”即试验数据,不能有缺失数据。
-
如果是DOE设计,那么其通常有两种编码,分别是‘实际值’和‘编码值’,在分析的时候,通常是使用‘编码值’,即使用0/1/2等表示不同水平的编码值。实际值有实际意义比如数字35表示温度这样的值。如果在RSM时放入的是‘实际值’,那么对应参数值应该选中‘“因子”进行数据编码’。如果RSM时放入的是‘编码值’,那么是否选中““因子”进行数据编码”两种情况均可。
关于模型参数设计,如下图和具体说明:
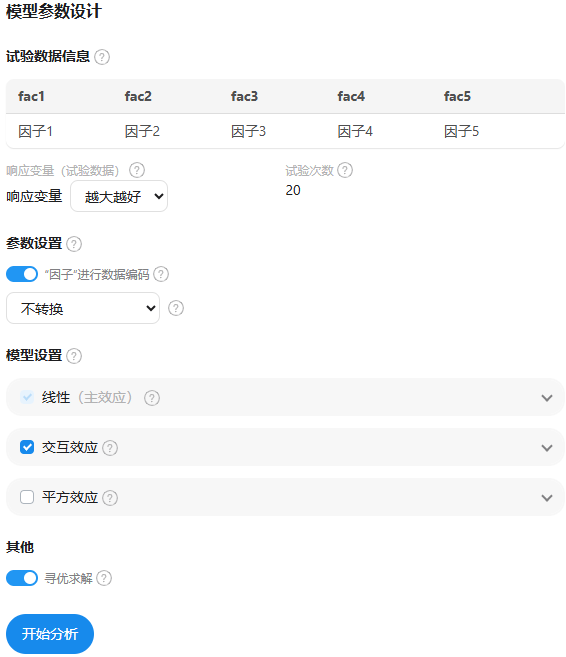
关于‘试验数据信息’
其展示自变量因子的名称即放入数据第1行的前n-1个名称,并且以fac1/fac2等进行命名。
关于‘响应变量’
其展示响应变量的名称,即放入数据第1行的最后1列名称,并且设置其方向,默认是该数据‘越大越好’,也可选择‘越小越好’。此参数对于‘寻优求解’会产生影响。
关于‘因子进行数据编码’
默认进行选中并且强烈建议进行选中,其目的是消除量纲影响。其针对每个因子进行编码后再纳入分析,其编码公式为:(X - 中位值)/((最大值-最小值)/2),中位数=(最大值+最小值)/2。简单来讲即先对放入的数据,以因子(即每列为单位)分别按照编码公式处理后再进行分析。
关于‘响应变量’数据转换
针对响应变量的转换上,默认是不进行转换,即将放入的数据直接纳入分析。当然可以进行一些转换设置,当进行转换后,SPSSAU会先对响应变量数据转换后再进行分析,并且在相关需要用到原始数据(转换前数据),比如响应变量的寻优求解时,SPSSAU会反转换计算后输出,便于分析人员使用。关于转换的各种类型,如下表格说明:
转换方式 计算公式 符号标识 默认值说明 平方根时 sqrt (y + k) SqrtRoot 默认K值=0 自然对数 ln (y + k) Ln 默认K值=0 10为底对数 log10 (y + k) Log10 默认K值=0 平方根反比 1 / Sqrt (y + k) InverseSqrtRoot 默认K值=0 倒数 1 / (y + k) Inverse 默认K值=0 Power幂 (y + k) ^λ Power 默认K值=0和λ值=1 Logit ln ( (y - lower) / (upper – y) Logit 默认Lower值 和 Upper值均为0 反正弦平方根 arcsin(sqrt(y)) ArcSquareRoot 无参数 SPSSAU提供8种响应变量转换方式,比如平方根时,k=0(默认也为0,可自行设置),那么响应变量会按照sqrt(y+k)即sqrt(y)即先求出响应变量的平方根后再纳入进行分析。并且在对应输出需要原始y处时,SPSSAU会先反转换回去。与此同时,为区分转换前和转换后,因而使用符号标识,比如转换后可能名称为:SqrtRoor(响应因变),以便于区分。
关于‘模型设置’
模型设置时,主效应是必须项,默认有交互效应,当然研究者可自行设置具体的交互效应项。以及二阶效应(平方效应)为可选项,以及研究者可具体设置某个或多个二阶效应是否纳入模型中。类似如下图:
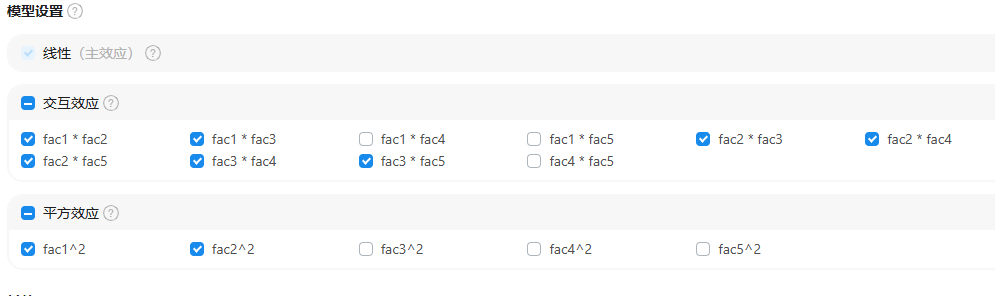
关于‘寻优求解’
寻优求解是指找出响应变量达到最优解时因子的不同水平组合,即找到最佳的因子水平组合时,响应变量达最优解。此处最优解可能是最大值(默认情况),也可能是最小值,其由响应变量的设置参数决定。
-
-
4、SPSSAU输出结果
SPSSAU中进行响应面分析时,其共输出7个表格和3类图,分别说明如下:
项 名称 说明 1 模型参数 基本参数情况说明等,第1个表格就是参数设置的展示 2 方差分析ANOVA结果 核心结果表格 3 响应曲面回归分析 核心结果表格 4 响应面回归拟合指标 响应面回归拟合指标结果值汇总 5 标准化效应Pareto图 虚线是 t(0.975,残差自由度)对应的临界值,用于判断对应项的显著性 6 模型寻优求解 根据参数‘优化求解’而定,不选中则没有该表格 7 模型分析数据 如果有编码则会展示编码后数据,以及拟合后得到的比如Y的拟合值数据等,展示编码后数据/残差/拟合值/杠杆值/cook值/dffit值等 8 模型原始数据 原始数据的展示 9 模型拟合效应图 使用模型分析数据进行绘图,研究者可自由下拉选择。就是用这些来自由绘图查看拟合效果等,比如残差的正态性,残差和拟合值的散点关系等 10 等高线图 等高线绘图,可结合下拉选择进行绘图,可下拉切换不同因子间的等高线图 -
提示:
-
如果纳入分析的数据无法拟合,比如共线性问题非常强导致无法拟合时,SPSSAU会输出‘模型共线性问题识别’表格,辅助研究者判断数据共线性问题,并且移去共线性问题项后再次分析(通常需要移出部分,交互效应或平方效应,因为共线性问题多数原因均是该2项导致)
-
-
5、文字分析

模型参数表格,其展示基本数据信息,比如分析包括20个试验样本,5个因子等;以及参数设置信息情况,包括响应变量的方向为‘越大越好’,并且对因子需要进行‘数据编码’,并没有对响应变量进行数据转换处理,以及需要是否需要进行寻优求解等。
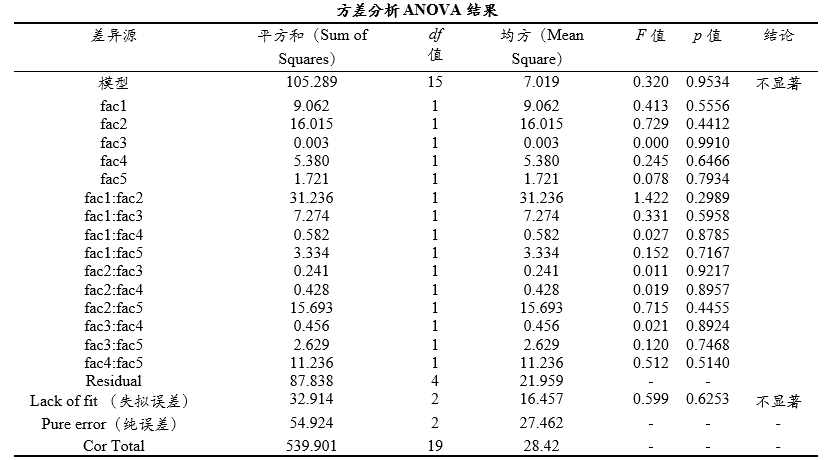
上表格是上表格展示响应面分析的核心结果方差分析结果;第1行即‘模型’,其反应整体模型(包含主效应、交互项和平方项等)对响应变量的解释情况,如果对应p 值呈现出显著性(比如小于0.05或0.01或0.1等),则表明模型整体显著,能有效解释响应变量的变异,反之如果没有呈现出显著性,则可能意味着模型无效;本次构建模型并没有呈现出显著性,那么意味着本次模型(主效应和交互项)均不会对响应变量产生解释作用,意味着模型意义较小,此时可考虑放弃一部分交互项甚至完全不要交互项后,重新进行分析,技巧上一般是把p 值较大的项不纳入分析即可。当然比如本次模型时fac3对应的p 值为0.9910较大也可以直接放弃该项。
失拟项(Lack of Fit),其意义为检验‘模型未解释的变异’是否显著大于‘实验误差’,即模型是否遗漏关键因素或存在结构缺陷),通常希望其对应p 值不需要呈现出显著性(即希望p 值>0.05),上图中显示p 值>0.05,即意味着不存在遗漏着急因素。
纯误差(Pure Error),其意义为实验中不可控的随机误差情况,通常意义较小;总离差(Cor Total),其意义为整体模型的变异,通常意义较小;
一般情况下,基于‘模型’呈现出显著性并且失拟项(Lack of Fit)不显著,这两个条件均满足时才能进一步分析主效应/交互效应/平方效应的显著性。本次仅为案例数据,‘模型’项并没有呈现出显著性,意味着需要重新构建模型。比如把fac3直接从模型中移出不分析。
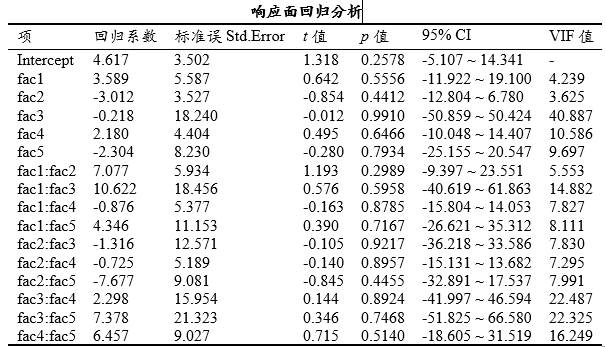
上图为响应面回归分析结果;响应面模型分析时,可从方差分析角度和回归分析角度分别研究效应项对于响应变量的作用情况,方差分析结果更多是检验效应项的显著性情况,即是否有显著影响,回归分析结果更多是从影响方向及影响幅度角度进行分析;
响应面回归分析的解读与线性回归表现出一致性,通常需要分析效应项的显著性,如果呈现出显著性,那么分析回归系数的方向(正数表示正向影响,负数表示负向影响),回归系数的大小表示影响幅度情况;
响应面回归分析时对于共线性问题的关注度较高,如果有发现VIF值较高,可考虑将该效应项移除后重新进行分析;比如上图中显示fac3和fac4对应的VIF值均大于10,尤其是fac3,那么可以先把fac3从模型中移出后再次分析。
响应面回归分析时也有各种拟合指标,在下表格中有具体呈现,包括RMSE、R 方值等,但关注度相对较低。需要说明的是:AIC和BIC通常用于模型选择时使用,该2个值越小时意味着模型越优。比如有多个模型需要对比优劣,那么可结合该2个指标进行,且该两个指标一般是越小越好。

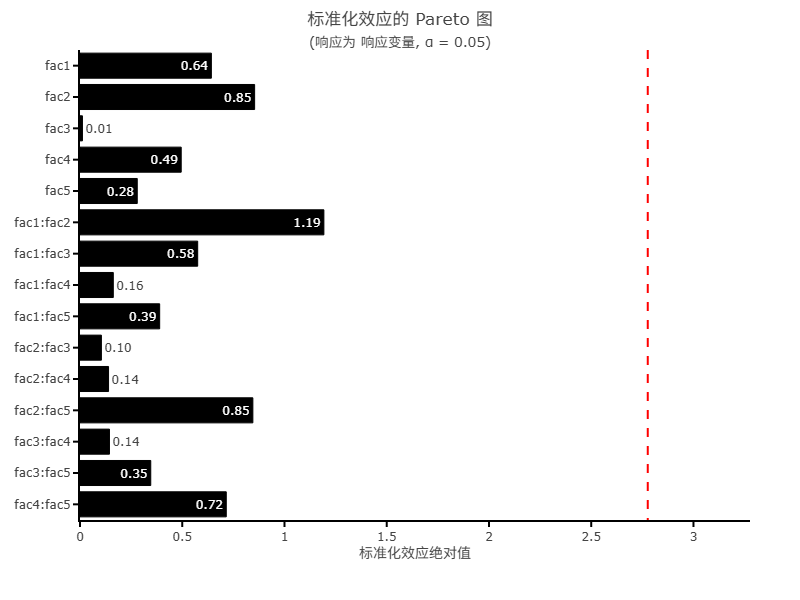
标准化效应图展示各效应项的回归系数t 值(其绝对值)与临界值对比,其目的是查看效应项的显著性情况,当柱子超过红色虚线(即临界值,0.05水平作为标准)时,意味着该项呈现出显著性,反之如果柱子没有超过临界值即意味着该项并没有呈现出显著性;与此同时,基于柱子呈现出显著性(即柱子超过红色虚线临界值时),此时柱子越长时意味着影响幅度会越大。标准化效应图的意义通常较小,但其可更直观地查看效应项的显著性情况。
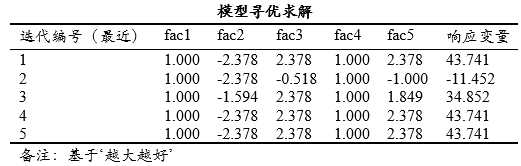
上表格展示出模型寻优求解的迭代过程(并且SPSSAU最多展示最近10次迭代过程)和最终结果,迭代过程表示主效应变量取不同数字水平时,响应变量的取值情况。本案例时响应变量越大越好,迭代5次后就达到最优解结果,即fac1取值为1,fac2取值为-2.378,fac3取值为2.378,fac4取值为1,fac5取值为2.378时,此时响应变量达到最优解,最优解数值为43.741。
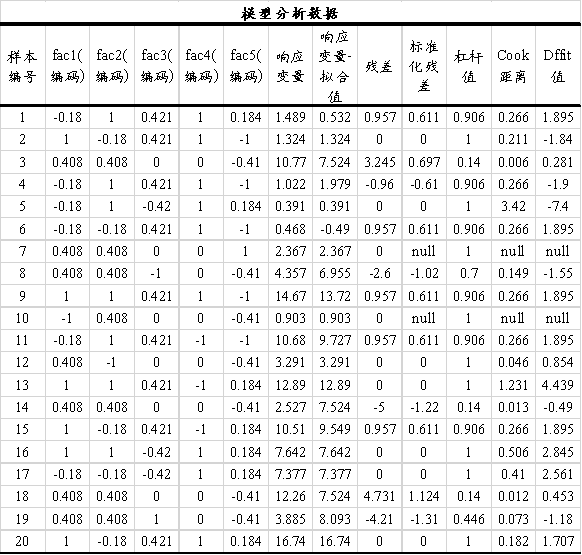
上图展示模型分析数据,由于选择了对因子编码,因此SPSSAU会对因子进行编码,其编码公式为:(X - 中位值)/((最大值-最小值)/2),中位数=(最大值+最小值)/2,并且在上表格中进行展示。与此同时,还展示出响应变量及其拟合值。模型得到的残差值、标准化残差值、杠杆值、Cook距离和Dffit值等,这些数据通常可进一步分析模型质量,比如对于标准化残差绘制直方图以查阅其正态性情况等,也或者查看残并和拟合值之间的散点关系用于分析模型质量等。比如下图为残差的直方图展示结果。
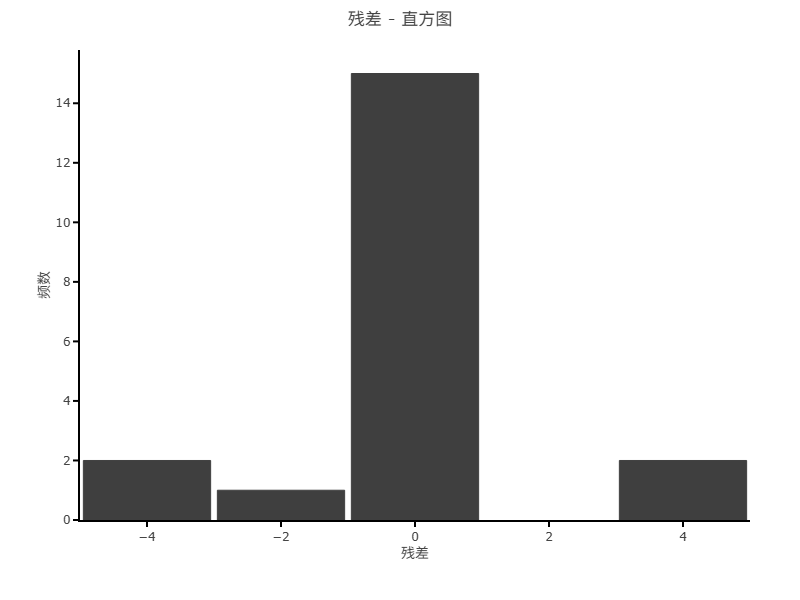
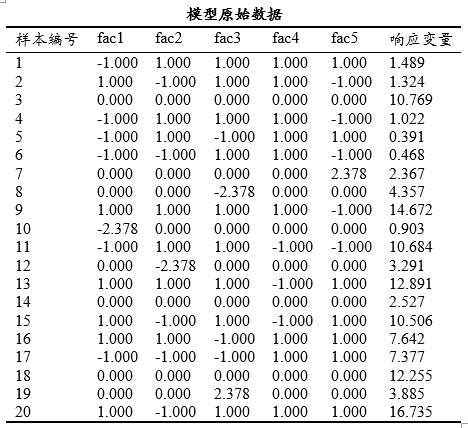
上图展示模型的原始数据,其无特别意义。
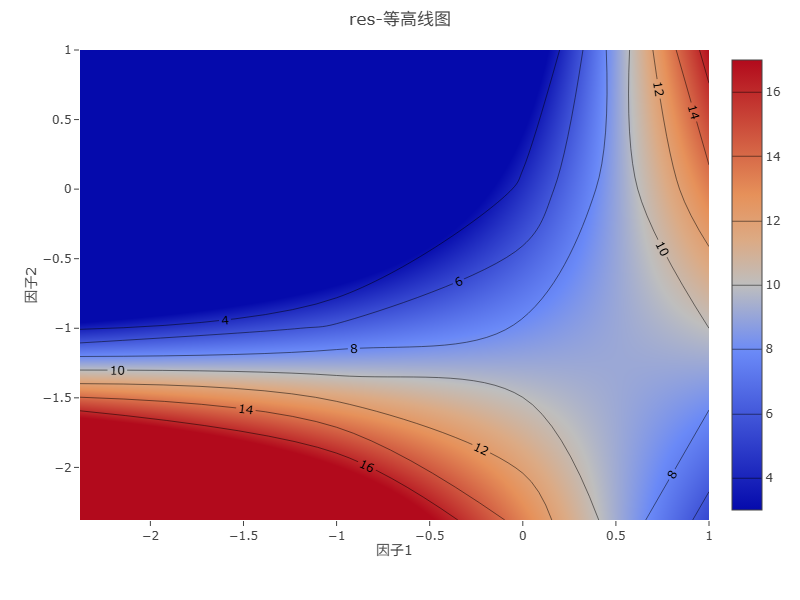
上图为等高线图,默认情况下,SPSSAU展示出因子1和因子2,并且基于其它因子位于中间值(中位数值)前提时的等高线图。
-
从上图可首先看出响应值分布特征情况:
-
左下角区域:呈现深红色,响应值较高(16-18),表明当因子1和因子2都处于较低水平时,响应值达到最大
-
右上角区域:呈现深蓝色,响应值较低(4-6),表明当因子1和因子2都处于较高水平时,响应值最小
-
中间区域:呈现渐变色,响应值从8到12不等,形成平滑过渡
-
接着等高线形态上:
-
等高线呈现出明显的非线性特征,特别是在左下角和右上角区域
-
等高线在左下角区域密集,表明该区域响应值变化剧烈
-
等高线在右上角区域稀疏,表明该区域响应值变化平缓
-
等高线整体呈S形曲线,说明两个因素之间存在显著的交互作用
-
关于‘最优区域识别’上:
-
最优区域位于左下角,即因子1和因子2都处于较低水平的区域
-
在该区域内,响应值达到最高水平(16-18)
-
随着因子1和因子2的增加,响应值逐渐降低
-
关于等高线的常见分析理论知识上:
-
等高线图可直观展示两个效应项之间交互作用下的响应值变化规律,其可辅助定位最优参数值组合。等高线表示两个效应项之间不同数值组合形成的‘相同响应值’,等高线的数字越大(颜色越红),此时表示该两个效应项之间不同组合形成更高的‘响应值’;
-
如果等高线呈弯曲或椭圆状,说明变量之间可能存在非线性关系或交互作用;如果等高线接近直线,说明变重之间的影响可能是线性的,且交互作用较弱或不存在;等高线在某区域内越密集时,意味着该区域内交互作用性越强;等高线图用于可视化两个效应项之间情况,并且基于其它效应变量在固定水平值前提时(研究者可自行设置)。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
响应面分析的数据从哪里来?
-
响应面分析时,其通常是由DOE设计并且收集到实验数据后进行分析,一般是BBD设计或者CCD设计,并且完成试验数据后得到。并且一般分析时使用BBD/CCD的编码数据。
-
响应面分析时出现共线性问题?
-
响应面分析时,模型中的变量(特别是交互项和平方项)很容易出现高度相关,其导致参数估计不稳定。此时建议将VIF值较大项从模型中直接移除出去,再次分析,SPSSAU默认有输出VIF值。
-