质量控制图
统计过程控制图(Statistical Process Control Chart)是一种用于监控生产过程稳定性的统计工具。通过绘制数据点在时间序列上的分布,帮助识别过程中的异常变化。统计控制图可实时监控生产过程是否处于统计控制状态,及时发现过程中的异常波动和趋势,为持续改进提供数据支持,以及可在问题发生前进行预警。SPSSAU中共支持9类统计控制图,分别是:Xbar-S/Xbar-R/Xbar/I-MR/I, P/NP/C/U图。涉及到连续(定量)和离散(定类)两种数据类型,如果是连续数据时区分是否包括子组两种数据格式,如果有子组数据则应该使用Xbar-S/Xbar-R/Xbar,如果没有子组数据则应该使用I-MR/I图,如果是离散(定类)数据,应该使用P/NP/C/U图。具体选择使用可参考下图:
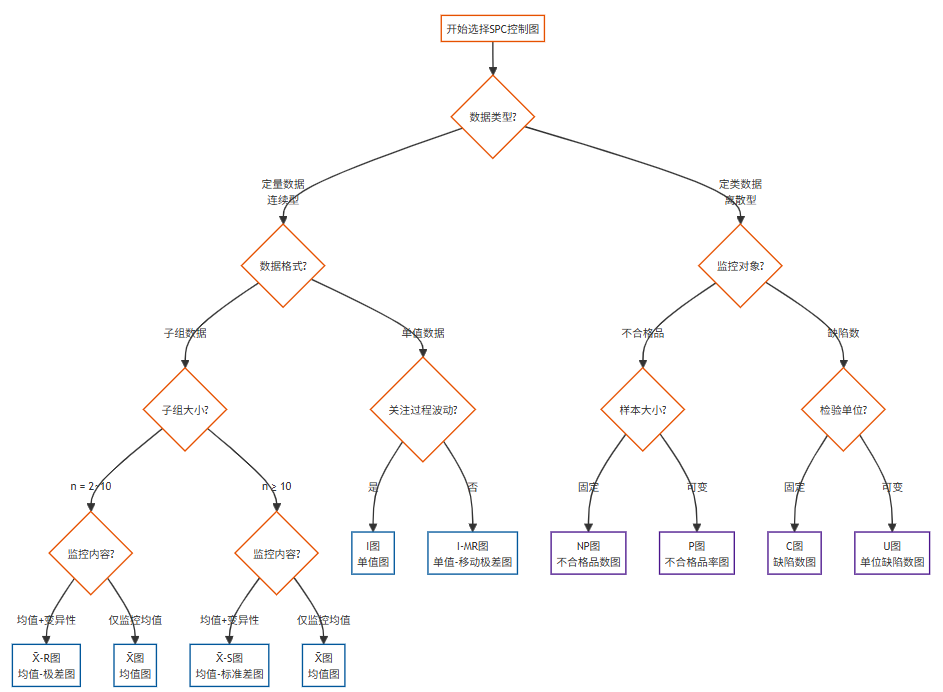
如果是监控连续性数据,那么应该选择Xbar-S/Xbar-R/Xbar/I-MR/I,继续区分数据格式,如果是子组数据那么应该选择Xbar-S/Xbar-R/Xbar,反之如果是单值数据则选择I-MR/I图。进一步似子组大小和监控目的而定,如果子组较少关注均值变异性,那么使用Xbar-R图,如果子组较大监控变异图可使用Xbar-S图,如果仅仅监控均值,那么使用Xbar图即可。单值数据并且关注数据波动时可使用I-MR图。
当数据是离散性,似监控对象而定,当关注不合格品时使用NP/P图,如果关注缺陷数则使用C/U图。进一步判断单位信息情况,比如基数大小固定时使用NP图(关注不合格品数),反之使用P图(关注不合格品率)。基数大小固定时可使用C图(关注单位内缺陷数),反之使用U图(关注缺陷率)。
质量控制图案例
-
1、理论
SPSSAU提供九类质量控制图,该九类的汇总说明,如下表所示:
控制图类型 数据类型 数据格式 子组大小 说明 X̄-S图 连续(定量) 子组数据 n≥10 过程均值+标准差,使用很多 X̄-R图 连续(定量) 子组数据 2≤n≤10 过程均值+极差,使用很多 X̄图 连续(定量) 子组数据 n≥2 仅监控过程均值 I-MR图 连续(定量) 单值数据 n=1 个别值+移动极差,无子组 I图 连续(定量) 单值数据 n=1 仅监控个别值,无子组 P图 离散(定类) 离散数据 可变 不合格品率 NP图 离散(定类) 离散数据 固定 不合格品数 C图 离散(定类) 离散数据 固定 缺陷数 U图 离散(定类) 离散数据 可变 单位缺陷率 如果是连续数据,并且子组数据格式,则应该选择使用Xbar-S/Xbar-R/Xbar图,并且结合子组大小和监控目的进一步进行选择。如果是连续数据并且是单值数据则应该使用I-MR或I图。当是离散数据时,可使用P/NP/C/U图,进一步判断,如果是单位基数固定和不固定两种情况,一种是监控‘数’,一个是监控‘率’,比如NP和C图分别关注不合格品数和单位缺陷个数,而P图和U图分别 关注不合格率和单位缺陷比率。
以及关于9种控制图的数学计算公式,分别如下述:
1) X̄-S图(均值-标准差图)
如果每次取的样本比较多(通常10个以上)时,用标准差比极差更准确。因为极差只看最大最小值,其忽略掉中间数据的变化,而标准差考虑了所有数据点。均值就是平均数,假设每次取5个零件测量长度,得到5个数据,把这5个数加起来除以5就是均值。
计算公式上:对于每组数据,先算出某组的平均值(均值),然后把所有组的均值再平均一次,得到总均值即控制图的中心线。同样,把所有子组的标准差平均一次,得到平均标准差。控制限就像是"警戒线",超出这条线就要注意了。以及下述中会提及A2、A3、B3、B4、D3、D4等这些SPC系数来计算控制限,这类系数是统计学家根据大量数据总结出来的标准值,不同的样本数量对应不同的系数。均值数和标准差图的控制限计算分别如下述:
-
X̄图:中心线=总均值,控制限=总均值 ± 3×(平均标准差/平均c4系数/√平均样本数)
-
S图:中心线=平均标准差,控制限=平均标准差 ± 3×(平均标准差/平均c4系数×√(1-平均c4系数2))
2) X̄-R图(均值-极差图)
X̄-R是最常见的控制图,适合每次取2-10个产品进行测量的情况。比如每小时从生产线上取5个零件测量尺寸,或者每批次取4个产品检测重量。
极差是最大值减最小值,假设每次取5个零件测量长度,得到5个数据,该5个数据的最大值的减去最小值的就是极差。
计算公式上:对于每组数据,先算出某组的平均值(均值),再算出最大值与最小值的差(极差)。然后把所有组的均值再平均一次,得到总均值即控制图的中心线。同样,把所有组的极差平均一次,得到平均极差。以及其控制限的计算说明分别如下述:
-
X̄图:中心线=总均值,控制限=总均值 ± 3×(平均极差/平均d2系数/√平均样本数)
-
R图:中心线=平均极差,控制限=平均极差 ± 3×(平均d3系数/平均d2系数×平均极差)
3) X̄图(仅均值图)
如果只关心平均水平,不太在意波动大小时使用。或者当过程的变异性已经很稳定,不需要再监控时,此时可只使用均值图。
计算公式上:计算各组数据的平均值,然后画成图表。控制限的计算需要借助极差或标准差的信息,或者使用已知的过程标准差。以及控制线计算如下述:
-
中心线=总均值(所有子组均值的平均)
-
控制限:总均值 ± 3×(总体标准差/√平均样本数)
4) I-MR图(单值-移动极差图)
如果每次只能得到一个测量值的情况,比如每天测一次温度、每批测一次pH值等。由于没有多个数据来计算极差,所以用"移动极差"的概念。移动极差就是相邻两个数据之间的差值。比如今天测得25度,昨天是23度,移动极差就是|25-23|=2度。
计算公式上:
-
I图:中心线=总均值,控制限=总均值 ± 3×标准差
-
MR图:中心线=平均移动极差,上限=3.267×平均移动极差,下限=0
5) I图(仅单值图)
I图仅监控单个测量值,其计算较为简单,如下述:
-
中心线=平均值
-
控制限:平均值 ± 3×标准差
6) P图(不合格品率图)
如果关心不合格品占总数的比例时使用,比如客户投诉率、产品缺陷率等。样本大小可以变化,比如这批检查了100个,下批检查了120个。
计算公式上如下述:
-
不合格品率 = 不合格品数/检查总数
-
中心线=总体不合格品率
-
控制限=总体不合格品率 ± 3×√[总体不合格品率×(1-总体不合格品率)/样本量]
7) NP图(不合格品数图)
如果每次检查的数量都相同,关心不合格品的绝对数量时使用。比如每天都检查100个产品,看有多少个不合格。
计算公式如下:
-
中心线=平均不合格品数
-
控制限=平均不合格品数 ± 3×√[平均不合格品数×(1-不合格品率)]
8) C图(缺陷数图)
如果每次检查的数量都相同,关心不合格品的绝对数量时使用。比如每天都检查100个产品,看有多少个不合格。
计算公式上如相:
-
中心线=平均缺陷数
-
控制限=平均缺陷数 ± 3×√平均缺陷数
9) U图(单位缺陷数图)
如果每次检查的数量都相同,关心不合格品的绝对数量时使用。比如每天都检查100个产品,看有多少个不合格。
计算公式如下:
-
单位缺陷数 = 缺陷总数/检查单位大小
-
中心线=加权平均单位缺陷数
-
控制限=平均单位缺陷数 ± 3×√(平均单位缺陷数/检查单位大小)
10) 关于SPC控制系数表
n d2系数 d3系数 c4系数 A3系数 2 1.128 0.853 0.7979 2.659 3 1.693 0.888 0.8862 1.954 4 2.059 0.88 0.9213 1.628 5 2.426 0.864 0.94 1.427 6 2.534 0.848 0.9515 1.287 7 2.704 0.833 0.9594 1.182 8 2.847 0.82 0.965 1.099 9 2.97 0.808 0.9693 1.032 10 3.078 0.797 0.9727 0.975 11 3.173 0.787 0.9754 0.927 12 3.258 0.778 0.9776 0.866 13 3.336 0.77 0.9794 0.85 14 3.407 0.763 0.981 0.817 15 3.472 0.756 0.9832 0.789 16 3.532 0.75 0.9835 0.763 17 3.588 0.744 0.9845 0.739 18 3.64 0.739 0.9854 0.718 19 3.698 0.734 0.9862 0.698 20 3.735 0.729 0.9869 0.68 21 3.778 0.724 0.9876 0.663 22 3.819 0.72 0.9882 0.647 23 3.858 0.716 0.9887 0.633 24 3.895 0.712 0.9892 0.619 25 3.931 0.708 0.9896 0.606 针对SPC控制系数列,如果n小于25时,SPSSAU使用上表格,如果n>25时,SPSSAU会自动进行额外计算,其计算公式如下:
当样本量n>25时,d2系数通过伽马函数积分法计算,即:d2(n) = √2 × Γ((n+1)/2) / Γ(n/2),d2系数用来将极差转换为标准差的估计值。当样本量超过25时,查表法不够精确,需要用数学积分公式来精确计算。这个公式基于统计学理论,通过伽马函数(Gamma函数)来描述极差分布的数学特性。
当样本量n>25时,d3系数通过近似公式计算:d3(n) = 0.886 / √n,d3系数用来计算极差本身的标准差。当样本量很大时,这个系数会随着样本量增加而减小,遵循"样本量越大,估计越稳定"的统计学原理。0.886是一个经过大量统计验证的常数,就像物理学中的重力加速度9.8一样,是通过理论推导和实验验证得出的固定值。
当样本量n>25时,c4系数通过伽马函数计算:c4(n) = √(2/(n-1)) × Γ(n/2) / Γ((n-1)/2),c4系数用来修正标准差的偏差,让标准差的估计更准确。在统计学中,直接计算的标准差往往会偏小,需要用c4系数来"校正"这个偏差。该公式确保了无论样本量多大,计算出的标准差都是无偏的(即长期平均下来等于真实值)。
当样本量n>25时,A3系数通过组合公式计算:A3(n) = 3 / (c4(n) × √n),A3系数专门用于X̄-S图(均值-标准差图)的控制限计算。它结合了c4系数的修正作用和样本量的影响。数字"3"代表3倍标准差的统计控制原理(99.7%的数据应该在3倍标准差范围内)。这个公式确保了控制限的计算既考虑了标准差的偏差修正,又考虑样本量对控制限宽度的影响。
-
-
2、操作
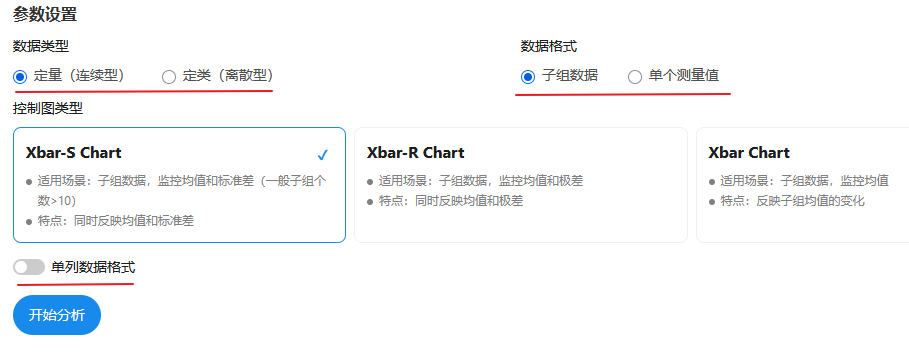
SPSSAU中进行质量控制图时,需要选择数据类型,数据格式(子组数据还是单个测量值),以及如果是子组数据时,需要确认具体子组的表示方式(单列还是多列)。
-
提示:
-
如果是单列数据格式需要设置‘子组大小’参数,比如有100个样本点,子组大小为5,那子组个数=100/5=20,设置子组大小后SPSSAU自动计算子组个数。如果是多列数据格式,格式上为‘一行表示一个子组’。
-
另:SPSSAU默认提供Demo数据,取消‘Demo数据’复选框后则清空默认数据,研究者粘贴实际数据到编辑框后,点击‘开始分析’即可。
-
-
3、SPSSAU输出结果
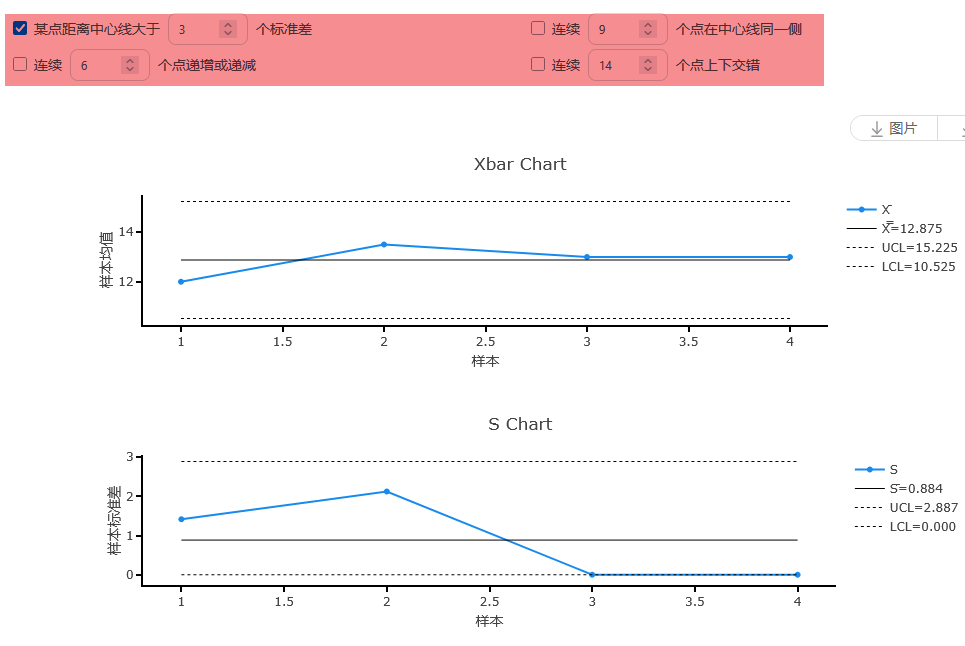
默认情况下,SPSSAU提供控制图,以及分析建议。与此同时,SPSSAU提供控制图时,其列出四项异常值监控方式,分别是距离中心线距离多少标准差(单点超出控制限),连续多少点在中心线同一侧(连续点偏向一侧),连续多少点在递增或递减(连续上升或下降趋势),连续多少点上下交错等共4种异常值检测,并且会在控制图中自动进行切换标识。
规则一:单点超出控制限,默认以超出3σ控制限(UCL或LCL)作为标准,正常过程中,数据点落在3σ外的概率仅为0.27%,研究者可自行进行切换修改该标准。此类点超出控制限时,一般意味着过程发生重大偏移。
规则2:连续点偏向一侧,默认以连续9个点落在中心线同一侧,一般情况下连续9点在同侧的概率为(1/2)^9 ≈ 0.2%。此类情况时,一般意味着过程均值发生系统性偏移。
规则3:连续上升或下降趋势,默认以连续6个点呈单调递增或递减作为标准。一般情况下6个点严格单调的概率为2/6! ≈ 0.28%。出现此类异常时,可能意味着过程存在渐进性趋势变化(如设备磨损)。
规则4:上下交错,默认以连续14个点在中心线上下交替出现作为标准。
-
4、剖析
涉及以下几个关键点,分别如下:
-
SPC控制系数是什么意思?
-
计算公式中会出现,比如d2、d3、c4和A3表等,其都是统计学家通过复杂的数学推导得出的标准系数。这些系数确保了控制图的准确性。当n<=25时,SPSSAU默认查表得到该类系数,当n>时,SPSSAU会自动计算,具体见本文档理论说明。
-
控制图异常值判断判断?
-
SPSSAU当前对控制图异常点判断上,默认提供四项异常值监控方式,分别是距离中心线距离多少标准差(单点超出控制限),连续多少点在中心线同一侧(连续点偏向一侧),连续多少点在递增或递减(连续上升或下降趋势),连续多少点上下交错。
-
清空Demo数据?
-
SPSSAU中进行控制图时,默认提供Demo数据,取消‘Demo数据’复选框后则清空默认数据,研究者粘贴实际数据到编辑框后,点击‘开始分析’即可。
-
子组数据的数据格式?
-
如果是单列数据格式需要设置‘子组大小’参数,比如有100个样本点,子组大小为5,那子组个数=100/5=20,设置子组大小后SPSSAU自动计算子组个数。如果是多列数据格式,格式上为‘一行表示一个子组’。
-