非线性回归
-
案例数据下载 下载
非线性回归是一种统计分析方法,用于描述自变量和因变量之间存在非线性关系的情况。与线性回归不同,非线性回归能够拟合更加复杂的函数形式,适用于那些无法用直线或平面准确描述的变量关系。在现实世界中,许多现象都表现出非线性关系,例如:年龄与工资的关系,药物剂量与治疗效果的关系,温度与化学反应速率的关系,广告投入与销售额的关系,生物种群增长模型。
-
提示:
-
SPSSAU中共提供三种非线性回归方式,分别是进阶方法模块中的曲线回归、非线性回归和质量控制模块中的非线性回归(自定义公式)。曲线回归仅提供二次曲线,三次曲线,对数曲线,指数曲线,复合曲线,增长曲线和S曲线共7种;非线性回归提供固定好的50种非线性函数表达式。SPSSAU推荐使用质量控制模块中的‘非线性回归(自定义公式)’,其高度支持自定义任意模型公式,且公式使用简单易懂。
非线性回归(自定义公式)案例
-
1、背景
当前希望研究年龄对于工资的影响,并且额外还有1个控制变量即教育,教育education使用1/2/3/4编码,分别表示本科以下、本科、硕士和博士共4种学位。研究时希望判断年龄和工资是否有着抛物线关系,即常见的工资先随着年龄上长,然后下降的这种非线性关系。预期的拟合模型公式为:Y = parm1 + parm2 * x1 + parm2 * x1^2 + parm3 *x2,其中Y表示工资Salary,x1表示年龄Age,x2表示教育水平Education,parm1/2/3/4表示需要拟合的4个参数值。
部分数据如下图所示:
-
2、理论
非线性模型数学原理上使用迭代算法进行寻优参数,SPSSAU自动选择最优的拟合结果,内部算法上可能合适到高斯-牛顿法(Gauss-Newton Method)、Levenberg-Marquardt算法等。
-
3、操作
本例子操作截图如下:
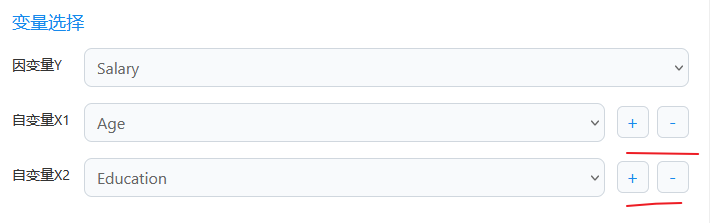
首先在左侧下拉选择变量Y和X,此案例的Y为薪水Salary,X为Age和Education。Age在模型里面也叫做X1,Education为X2。接着输入公式,即:Y = parm1 + parm2 * x1 + parm2 * x1^2 + parm3 *x2,其中Y表示工资Salary,x1表示年龄Age,x2表示教育水平Education,parm1/2/3/4表示需要拟合的4个参数值。
公式可以手工输入,也或者在仪表盘处进行选择,无论如何,SPSSAU会自动校验和提示公式的输入准确性情况。
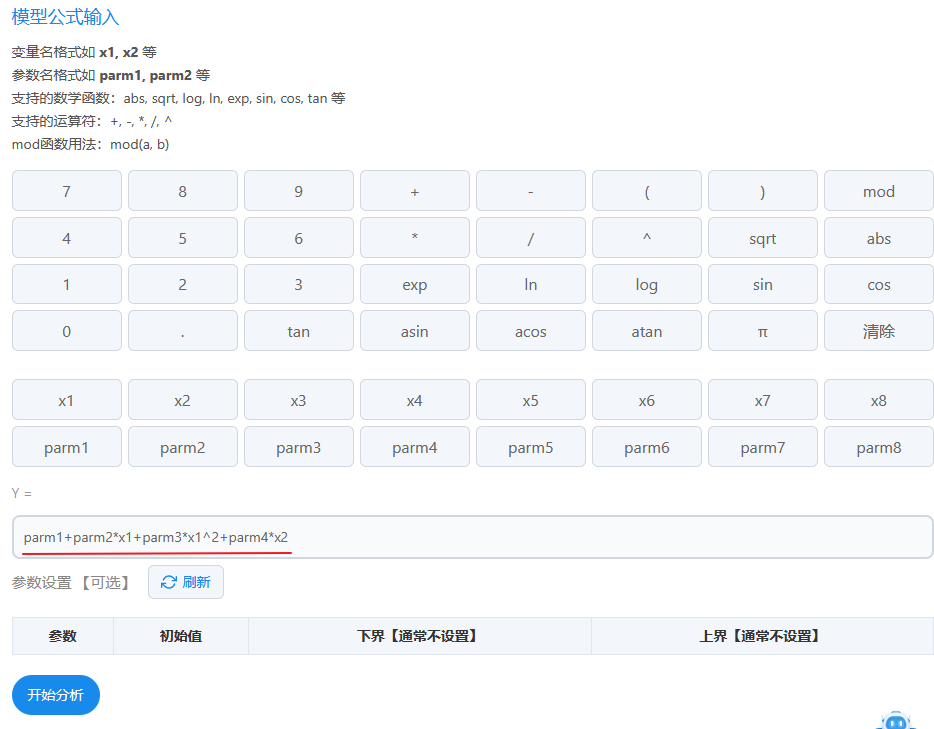
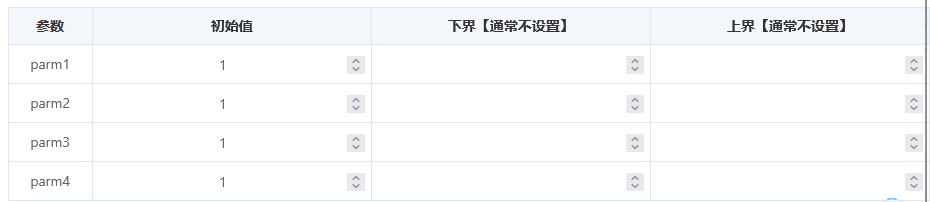
输入完成公式后,可直接进行‘开始分析’即可得到结果。当然也可以设置设置参数,点击‘刷新’按钮,SPSSAU会自动拉取出全部参数名称,研究者可自行设置初始值/下界和上界值,然后开始分析即可,本案例暂不设置参数,以及本案例时共有4个参数,因而下拉出4个参数值如下。
-
特别提示:
-
SPSSAU进行非线性回归时,其对公式的格式要求,说明如下:
-
因变量Y默认为等号左边
-
变量名格式:x1, x2, x3, ...
-
参数名格式:parm1, parm2, parm3, ...
-
支持的数学函数:abs, sqrt, log, ln, exp, sin, cos, tan, asin, acos, atan, mod
-
支持的运算符:+, -, *, /, ^(幂运算)
-
示例公式:1+sin(x1)+parm1*x2
-
-
4、SPSSAU输出结果
SPSSAU中进行非线性回归(并且自定义公式)时,共输出5个表格和1个拟合图,如下述:
项 说明 模型初始参数 展示模型初始参数的设置情况,如果不设置初始值则默认为1 模型参数估计值 非线性回归的核心表格即参数估计值结果,并且展示出拟合参数的显著性等 参数估计值的相关性 参数相关矩阵结果,其可用于查看共线性问题 模型拟合效果 模型拟合效果汇总表格,提供F检验和R方值等 模型拟合散点图 模型拟合散点,可分别查看不同的X与Y之间的散点效果 样本缺失情况汇总 展示真实进入算法的数据情况 除此之外,SPSSAU还提供页面进行预测的功能,输入X的信息,可得到预测的Y值。当然研究者可对得到的模式函数公式进行自主计算(提示:此处需要注意拟合参数的小数位精度问题)。
-
5、文字分析
模型初始参数 参数项 初始值 下界 上界 parm1 1.000 - - parm2 1.000 - - parm3 1.000 - - parm4 1.000 - - 上表格展示NLS非线性回归时可设置初始值,以及初始值的上下界值。初始值设置有助于模型正常且快速收敛,通常可结合专业知识、简单数学计算等确认初始值;如果不设置初始值,则默认为1;参数的上下界范围值,一般不需要进行设置。
模型参数估计值(n =100) 参数项 回归系数 标准误 t 值 p 值 95% CI parm1 36247.402 12231.730 2.963 0.004 11967.611 ~ 60527.194 parm2 2852.553 657.872 4.336 0.000 1546.688 ~ 4158.418 parm3 -111.210 8.275 -13.439 0.000 -127.636 ~ -94.785 parm4 397.544 949.590 0.419 0.676 -1487.377 ~ 2282.465 上表格展示出模型的参数值情况;从上表可知,模型公式为:Salary = 36247.402+2852.553*Age+(-111.210)*Age**2+397.544*Education。
参数parm1为36247.402,95% CI为11967.611 ~ 60527.194,不包括数字0,意味着其呈现出统计学意义。但此处parm1并无实际意义,其有点类似于线性回归的‘常数’,可类比为‘工资的基础值’,其无特别实际意义因而不需要分析。
参数parm2为2852.553,95% CI为1546.688 ~ 4158.418,不包括数字0,意味着其呈现出统计学意义。也即说明年龄对于工资有着正向的线性影响关系,年龄越大通常工资越高。
参数parm3为-111.210,95% CI为-127.636 ~ -94.785,不包括数字0,意味着其呈现出统计学意义。parm3表示工资的平方项的回归系数,其呈现出负数,也即说明年龄与工资之间呈现出抛物线平方项关系,而且为负数,即是一个“倒 U 型”关系,意味着工资随着年龄先上升,达到一个峰值后开始下降。常见于很多职业路径:年轻时工资增长快,中年达到顶峰,老年可能因退休或工作能力下降而减少。
参数parm4为397.544,95% CI为-1487.377 ~ 2282.465,包括数字0,意味着其没有呈现出统计学意义。parm4代表学历的回归系数,其没有呈现出显著性意味着此案例时学历对于工资并无显著影响作用。
参数估计值的相关性 parm1 parm2 parm3 parm4 parm1 1.000 -0.976 0.953 -0.066 parm2 -0.976 1.000 -0.990 -0.072 parm3 0.953 -0.990 1.000 0.025 parm4 -0.066 -0.072 0.025 1.000 上表格为参数相关矩阵(协方差矩阵)表格;相关矩阵表格中的数字表示两两参数之间的相关关系情况,其通常用于分析参数之间的共线性问题,如果该值的绝对值较大(比如0.8),即意味着该两项之间的相关性很强;当参数之间的相关性较强时,可能导致参数估计不稳定,以及模型解释性较低(即参数的数字意义无法描述和解释),此时可考虑移除其中一个参数即重新输入模型公式后再次进行分析。
从上表格可以看到:parm1、parm2、parm3之间均有着较强的共线性(系数绝对值大于0.8),此时可考虑把parm1这个参数移除出模型再次进行分析。本次仅作为SPSSAU案例演示非线性回归使用,并不进一步讨论和操作分析。
模型拟合效果 差异源 平方和SS df 均方MS F p值 回归 599981681154.733 4 149995420288.683 1481.766 0.000 残差 9717834918.177 96 101227447.064 未校正总计 609699516072.910 100 校正总计 487448193945.932 99 备注:模型R 方 = 0.980 模型拟合效果表格用于判断模型拟合效果情况;R 方值用于分析模型拟合情况;F 检验辅助判断模型的拟合效果(但其已经失去线性回归的意义);除此之外,可结合模型拟合图辅助判断模型拟合效果情况。
上表格中显示R 方值为0.980非常高,模型拟合非常理想,以及还可通过散点图查看X与Y之间的散点关系情况。如下图:
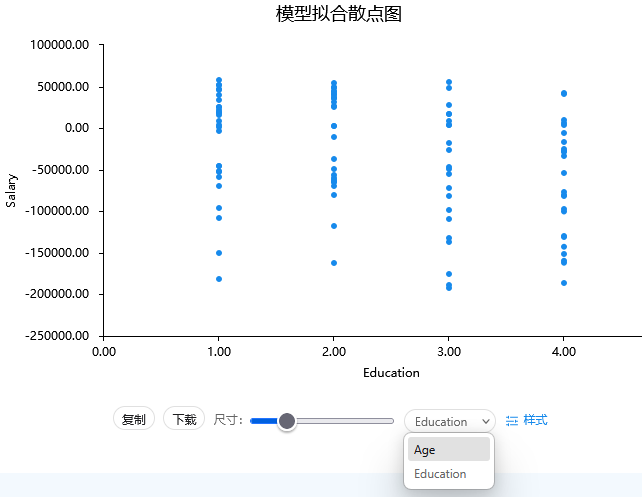
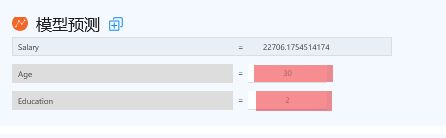
除此之外,SPSSAU还提供模型预测功能,比如下图时输入年龄为30岁,education为2即表示为本科时,其得到的工资为22706元。
-
提示:
-
研究者也可自行结合公式进行手工计算,但需要注意小数位精度问题,建议让SPSSAU呈现出20位小数的精度后在EXCEL中手工进行计算以获得准确预测结果。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
非线性回归的公式如何编号?
-
变量必须从x1开始连续使用(如使用x3则必须有x1和x2)
-
参数必须从parm1开始连续使用
-
函数名与括号之间不能有空格(如sin(x1)而不是sin (x1))
-
数字与变量之间必须有运算符(如2*x1而不是2x1)
-
括号必须匹配且不能嵌套超过3层
-
提示"公式必须包含至少一个变量(x1)"?
-
SPSAU自动校验公式的正确性并且进行提示,原理上每个非线性回归模型必须包含至少一个自变量,且SPSSAU规定必须从x1开始。
-
为什么提示"在xxx和xxx之间缺少运算符"?
-
SPSSAU中进行非线性回归定义公式时,规定变量、参数和常数之间必须用运算符连接,如parm1*x1而不是parm1x1。
-
SPSSAU中非线性回归时参数设置的意义?
-
默认情况下,SPSSAU进行非线性回归时,不需要主动设置参数,但如果出现拟合不出结果也或者结果与实际预期差别很大时,可考虑主动设置参数,设置参数时需要注意下述几点:
-
初始值应尽量接近真实值以提高收敛速度
-
如对参数范围有先验知识,可设置上下界
-
对于收敛困难的模型,可尝试不同的初始值
-
SPSSAU中如何提高非线性回归模型的拟合成功率?
-
拟合非线性回归时,有可能出现拟合不出结果的情况。此时建议从三个方面进行查看或设置,分别是合理设置参数初始值,设置合适的函数形式和设置参数边界。参数的初始值是一个心理大概猜想的数字,函数形式对于模型拟合至关重要,并且可设置参数的边界最小或最大值。
-
函数公式一样,但非线性回归和线性回归结果不一样?
-
如果说函数公式完全一样,但是非线性回归和线性回归出来的参数结果并不相同,这是正常现象,原因在于优化算法不同,非线性拟合使用迭代优化算法,其可能受初始值影响,收敛到局部最优,线性回归则是解析解,唯一且稳定。
-