过程能力分析

• 1、理论

  过程能力分析（Process Capability Analysis）是质量管理中的核心工具之一，用来衡量一个生产或业务过程是否能够稳定地满足客户或规范的要求。比如：产品尺寸或者性能是否稳定，是否持续满足客户要求的精度范围内，是偶尔合格还是一合格。

  过程能力分析包括短期能力和长期能力两类结果，短期过程能力是基于子组内部数据（如同一批次或时间段）评估过程在受控状态下的自然波动能力。长期过程能力是基于整个过程周期内的全部数据（跨批次、跨时间段）评估过程的总体波动性。短期能力和长期能力测量指标不尽可能，相关指标的计算公式和说明分别如下述：

  指标	计算公式	说明
  标准差（σ）	用每个数据与平均值的差距计算波动，公式为S-bar/c4	产品波动有多大，越小越稳定
  Cp（潜在过程能力指数）	(上限 - 下限) ÷ (6 × 标准差)	“理论上”有多准
  CPL（下限过程能力指数）	(平均值 - 下限) ÷ (3 × 标准差)	下限方向的能力，越大越好
  CPU（上限过程能力指数）	(上限 - 平均值) ÷ (3 × 标准差)	上限方向的能力，越大越好
  Cpk（实际过程能力指数）	CPL 和 CPU 中的较小值	“实际上”有多准，考虑偏移
  Cpm（考虑目标值偏离的过程能力指数）	(上限 - 下限) ÷ [6 × Sqrt(标准差² + (平均值 - 目标值)²)]	考虑目标值的能力，偏离目标会扣分
  PPM_below	正态分布计算低于下限的概率 × 100万	每百万个产品中低于下限的数量，越小越好
  PPM_above	正态分布计算高于上限的概率 × 100万	每百万个产品中高于上限的数量，越小越好
  PPM_total	PPM_below + PPM_above	每百万个产品中不合格的总数量

  上表格是短期能力相关指标，在短期过程能力分析中，我们通过一系列统计指标来评估过程的稳定性与精度。首先，标准差（σ）是衡量产品波动性的核心指标，它反映每个数据点与平均值之间的差距，标准差越小，说明过程越稳定。基于标准差，我们可以计算Cp，它表示过程在“理论上”有多精准，即规格范围与过程波动的比例，越大越好。

  进一步地，CPL 和 CPU 分别衡量过程在下限和上限方向的能力，若过程偏离中心值，这两个指标会不一致。Cpk 是 CPL 和 CPU 中的较小值，用来反映过程的“实际”能力，考虑了偏移因素。而 Cpm 则进一步引入目标值，如果过程均值偏离目标，它会扣分，因此更适合用于目标导向型质量评估。

  除了能力指数，我们还关注不合格品的概率。PPM below 和 PPM above 分别表示每百万个产品中低于下限或高于上限的数量，PPM total 是它们的总和，代表整体不合格率。这些指标基于正态分布计算，能直观反映过程输出的质量水平。短期 PPM 是基于组内标准差计算得到，其假设过程处于稳定状态，仅考虑自然波动。

  指标	计算公式	说明
  标准差（σ）	用所有数据计算整体波动	长期来看产品波动有多大
  Pp（总体潜在过程能力指数）	(上限 - 下限) ÷ (6 × 标准差)	理论能力（长期版本的 Cp）
  PPL（总体下限潜在过程能力指数）	(平均值 - 下限) ÷ (3 × 标准差)	长期下限方向的能力，越大越好
  PPU（总体上限潜在过程能力指数）	(上限 - 平均值) ÷ (3 × 标准差)	长期上限方向的能力，越大越好
  Ppk（总体实际过程能力指数）	PPL 和 PPU 中的较小值	长期实际能力，考虑偏差，越大越好
  PPM_below	正态分布计算低于下限的概率 × 100万	每百万个产品中低于下限的数量（长期），越小越好
  PPM_above	正态分布计算高于上限的概率 × 100万	每百万个产品中高于上限的数量（长期），越小越好
  PPM_total	PPM_below + PPM_above	每百万个产品中不合格的总数量（长期）

  长期过程能力分析关注的是过程在较长时间跨度内的整体表现，它考虑了所有数据的波动，包括组间差异、偏移和特殊原因。首先，标准差（σ）在这里是基于全体数据计算的，用于衡量过程在长期运行中的整体波动性。在此基础上，Pp 指标衡量过程的理论能力，是 Cp 的长期版本，反映规格范围与总体波动的比例。

  为了更细致地评估过程在不同方向上的能力，PPL 和 PPU 分别表示过程在下限和上限方向的长期能力。若过程偏离中心值，这两个指标会不一致。Ppk 是 PPL 和 PPU 中的较小值，用于衡量过程的实际长期能力，考虑了偏移因素，是客户验收和质量评估的重要依据。

  此外，长期能力分析也关注不合格品的概率。PPM_below 和 PPM_above 分别表示每百万个产品中低于下限或高于上限的数量，PPM_total 是它们的总和，反映整体不合格率。这些指标基于正态分布计算，能直观呈现过程在长期运行中的质量水平和风险。长期 PPM 则使用总体标准差进行计算，反映过程在实际运行中所有波动的影响。

• 2、操作

  假设某工厂生产一种精密零件，其关键尺寸规格要求为 600±5mm，即规格下限(LSL)为595mm，规格上限(USL)为605mm，目标值(Target)为600mm。为了评估该生产过程的能力，我们收集了10个样本数据进行分析，子组大小是5，即共有2个子组【提示，此为案例demo数据，实际研究中子组个数通常较多比如大于20】。本例子操作截图如下：

  

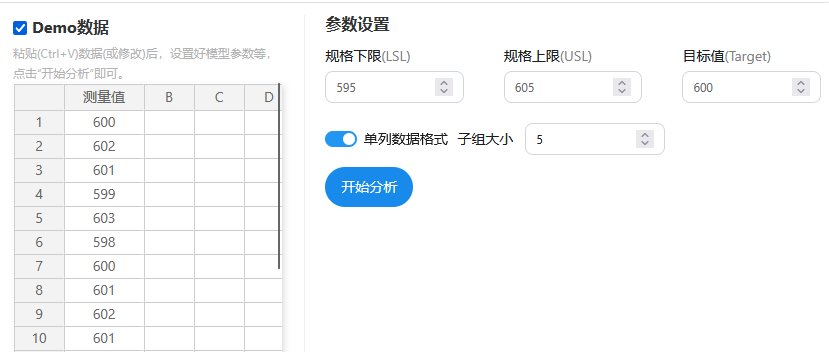
  上图中有设置目标值，该值为可选值，如果不设置则不会计算Cpm指标。

  • 提示：

  • SPSSAU支持两种格式，分别是单列数据格式（默认）和多列数据格式。单列数据格式时需要指定子组大小（2~100之间），默认是5，系统结合单列数个数计算出子组个数（比如100个数字，子组大小为5，那么子组个数=100/5=20）；如果是多列数据格式，1行表示1个子组，第1行的数字个数即为子组大小。

• 3、SPSSAU输出结果

  SPSSAU共输出5个表格和图形，下述：

  项	说明
  基本信息	描述输入指标，子组个数和子组大小基本信息等
  短期过程能力	包括Cp, Cpk等短期能力指标
  长期过程能力	包括Pp, Ppk等长期能力指标
  正态性检验	输入正态性检验指标
  直方图	可视化展示数据正态性情况
  PP图	可视化展示数据正态性情况

  在 SPSSAU 的过程能力分析结果中，基本信息表提供输入参数的概览，包括子组数量、子组大小等，为后续分析奠定基础。接着，系统分别输出短期过程能力指标（如 Cp、Cpk）和长期过程能力指标（如 Pp、Ppk），用于评估过程在不同时间尺度下的稳定性与精度。除此之外，SPSSAU还提供正态性检验结果，帮助用户判断数据是否符合正态分布。配合检验结果，系统自动生成直方图和PP图，以图形方式直观展示数据分布情况，便于用户快速识别偏态、离群点或分布异常。

  在过程能力分析中，结合短期与长期能力指标可以全面评估生产过程的稳定性与合格率表现。短期能力指标如 Cp 和 Cpk 反映过程在受控状态下的潜力与实际表现，而长期能力指标如 Pp 和 Ppk 则揭示过程在整体运行周期中的真实波动情况。通过对比这两类指标，企业可以判断过程是否稳定、是否存在特殊原因变异，以及是否需要调整工艺参数。

  具体而言，Cp 值用于衡量过程的潜在能力，其参考标准如下：Cp ≥ 1.67 表示过程能力非常充足；1.33 ≤ Cp < 1.67 表示能力充足；1.00 ≤ Cp < 1.33 表示能力尚可，需改进；Cp < 1.00 则说明能力不足，必须优化工艺。若 Cp 与 Cpk 相等，说明过程中心与规格中心一致，过程稳定；若 Cp 大于 Cpk，则说明过程存在偏移，需调整中心值。

  此外，若 Cp 与 Pp、Cpk 与 Ppk 基本一致，说明过程在短期与长期表现一致，具备稳定性。反之，若 Cp 明显大于 Pp，则可能存在特殊原因变异，需进一步调查与控制。通过这些指标的综合分析，企业可实现对过程质量的精准诊断与持续改进。

  • 提示：

  • SPSSAU进行能力研究时，直接通过粘贴或者编辑形式放入数据（不支持上传），如果研究时发现数据严重不正态，此时需要做处理比如做Box-Cox变换或Johnson转换等，需要先上传数据到SPSSAU中，通常生成变量处理后得到数据，然后下载粘贴到编辑框进行能力研究。

  

  上表格展示输入的规格下限和上限，目标值等基本信息。数据共10个点，子组个数是2个，每个子组大小为5。

  

  从上表格可知：短期能力时标准差为 1.595，说明过程存在一定波动，属于中等偏上的水平。在此基础上，Cp 值为 1.045，表示过程的理论能力略高于最低合格线（1.00），但仍有较大的优化空间。进一步分析 CPL（1.191）与 CPU（0.899）可以看出，过程在下限方向的能力较强，而在上限方向偏弱，说明过程中心偏向上限。Cpk 取 CPL 与 CPU 的较小值，即 0.899，反映出过程实际能力不足，偏移影响明显，无法稳定满足规格要求。

  Cpm 值为 0.957，考虑了目标值偏离的影响，进一步确认过程中心与目标存在一定偏差。在不合格率方面，PPM_below 为 176.315，PPM_above 高达 3512.888，总不合格率 PPM_total 为 3689.203，说明大部分不合格品集中在上限方向，与 CPU 值偏低相吻合。

  综述，该过程在理论上具备一定能力，但实际表现受偏移影响较大，尤其在上限方向存在明显质量风险。建议通过调整过程中心、优化工艺参数或缩小波动范围，以提升 Cpk 和降低 PPM，从而实现更稳定的质量输出。

  

  从上表可知，长期能力时标准差为 1.494，说明该过程存在一定的波动性，略低于前一组数据（1.595），表明过程在稳定性方面有所改善，但仍未达到高度稳定的水平。Pp 值为 1.115，表示过程总体能力略高于最低要求（1.00），具备一定的潜力。PPL（1.271）高于 PPU（0.959），说明过程在下限方向控制较好，而在上限方向偏弱，存在偏移现象。Ppk 取 PPL 与 PPU 的较小值，即 0.959，反映出过程实际能力受偏移影响，尚未达到理想状态。PPM_below 为 68.349，PPM_above 高达 2005.261，总不合格率 PPM_total 为 2073.610，说明大部分不合格品集中在上限方向，与 PPU 值偏低相一致。这种偏移可能导致产品超出规格上限，影响整体质量。

  该过程在总体能力上略有优势，但偏移问题仍然明显，特别是在上限方向。建议通过调整过程中心、加强上限控制、优化工艺参数，进一步提升 Ppk 值并降低 PPM，从而实现更高质量的过程输出。

  

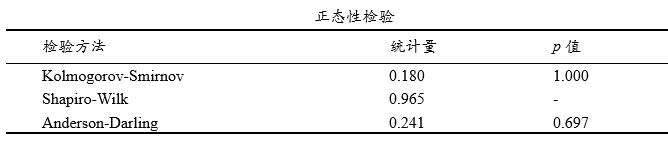
  上表格展示数据的正态性结果，默认情况上过程能力分析是基于正态性前提进行，SPSSAU提供3种检验分别是KS、SW和Anderson-Darling检验结果（该3检验的原假设为数据具有正态性，因而p 值>0.05则意味着数据具有正态性），表格显示p 值>0.05，意味着数据具有正态性。与此同时，SPSSAU还提供直方图和PP图，可通过图示直观查看数据正态性情况。

  

  

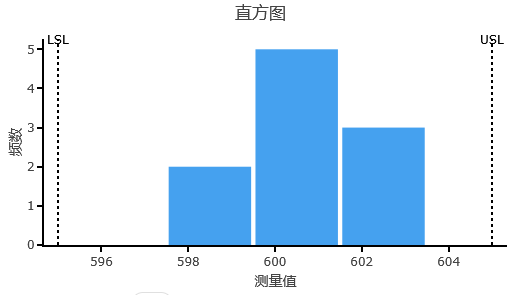
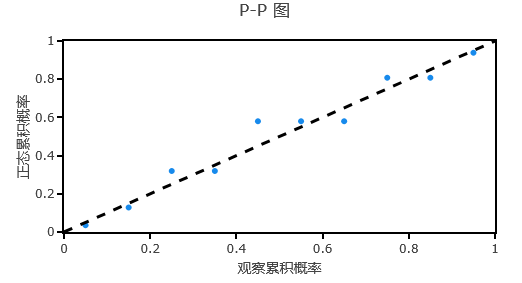
• 4、剖析

  涉及以下几个关键点，分别如下：

  • SPSSAU进行过程能力分析时支持的数据格式？

  • SPSSAU支持两种格式，分别是单列数据格式（默认）和多列数据格式。单列数据格式时需要指定子组大小（2~100之间），默认是5，系统结合单列数个数计算出子组个数（比如100个数字，子组大小为5，那么子组个数=100/5=20）；如果是多列数据格式，1行表示1个子组，第1行的数字个数即为子组大小。

  • 过程能力研究时，短期组内标准差和长期标准差的计算？

  • 组内标准差衡量每个子组内部样本之间的波动，其反映过程在短时间内的自然波动（如同一批次、同一时间点），其适合用于 Cp/Cpk 的计算。长期标准差衡量整个数据集的总波动性，包括组间偏移和特殊原因，其更贴近客户实际体验，适用于 Pp/Ppk 的计算。

  • SPSSAU进行过程能力研究时，组内标准差计算使用平均标准差法即组内标准差= S-bar/c4这一公式，长期标准差公式为所有样本点的标准差值。

  • SPSSAU进行过程能力分析时子组是什么意思？

  • 比如：每小时抽取5个产品进行测量，连续测量4小时，共20个数据，可以将每小时的5个产品作为一个子组，子组大小为5，共4个子组。也或者：每个批次生产100个产品，从每个批次中随机抽取5个产品测量，测量了6个批次，共30个数据，每个批次作为一个子组，子组大小为5，共6个子组。

  • 多数情况下，子组个数通常大于25个，子组大小（即每个子组的样本点通常为4~10个之间）。当子组个数少于 20 时，分析结果可能偏差较大。