朴素贝叶斯模型
-
案例数据下载 下载
贝叶斯模型是利用先贝叶斯定理进行计算的一种机器学习模型,并且此处涉及先验概率和后验概率。比如我们都知道去赌场会十赌九输,此是以前的经验,即为先验概率,也或者大家都知道抛硬币时上下面第一次都是1/2概率,这均为先验概率;如果发现一个人准备跳楼,那么此时他是因为赌博导致的概率是多少?此为后验概率。有了先验概率和后验证概率理解,结合贝叶斯定量即可计算出概率信息值。
接着,朴素贝叶斯是基于贝叶斯定量,并且加上条件(特征之间独立)的一种模型。此处特征属性之间独立是指比如:有100个数据,第1行数据与第2行,第3行等其它任意行数据之间并没有关系,此前提条件非常重要,但现实中较难成立,但这并没有妨碍其的广泛使用,可能原因在于朴素贝叶斯模型通于分类问题处理,其内部算法上会关注于条件概率排序并非具体概率数字,因而其具有一定容错能力,并且特征属性之间假如有着关系并不完全独立,其内部可能存在相关抵消现象。整体上看,朴素贝叶斯模型原理较为简单,且应用较为广泛,比如输入法时可能会进行纠错功能处理,也或者垃圾邮件的识别等。
朴素贝叶斯模型案例
-
1、背景
案例数据依旧采用‘鸢尾花分类数据集’,其数据集为150个样本,包括4个特征属性(4个自变量X),标签为鸢尾花卉类别,其分为3个类别分别是刚毛鸢尾花、变色鸢尾花和弗吉尼亚鸢尾花(下称A、B、C三类)。
-
2、理论
朴素贝叶斯模型的原理较为简单,其利用贝叶斯概率公式,分别如下:
接着假定各特征属性独立,并且将公式进行展示成如下:
关于朴素贝叶斯模型时,其原理理解较为简单,但其内部算法上有着更多内容,感兴趣的读者可参阅下述页面,点击查看。
关于朴素贝叶斯参数上,其特征(自变量X)的数据分布对模型有着较大影响,如下表格说明:
参数 说明 参数值设置 特征分布类型 特征项(自变量X)的分布类型 高斯分布:默认,大多数分布都是高斯分布。
伯努利分布:特征值取0和1的伯努利分布。
多项式分布:特征值取多个离散值的分布。如果特征即自变量X全部均为连续定量数据,那么选择高斯分布即可(此为默认值);如果说特征即自变量X中全部均是定类数据且每个X的类别数量大于2,此时可选择多项式分布。如果每个特征全部都是0和1共两个数字,此时选择伯努利分布。如果特征中即包括连续定量数据,又包括定类数据,建议可对定类数据进行哑变量设置后,选择高斯分布。
关于关于哑变量可点击查看。
-
3、操作
本例子操作如下:
训练集比例默认选择为:0.8即80%(150*0.8=120个样本)进行训练朴素贝叶斯模型,余下20%即30个样本(测试数据)用于模型的验证。需要注意的是,此处不进行处理也可以,尤其是自变量X中有定类数据是,建议默认不进行处理。
接着对参数设置如下:

本案例时四个自变量X(特征项)均为连续数据,因而默认为高斯分布即可;如果数据中包括定类数据,建议参考上一部分内容说明。
-
4、SPSSAU输出结果
SPSSAU共输出5项结果,依次为基本信息汇总,训练集或测试集模型评估结果,测试集结果混淆矩阵,模型汇总表和模型代码,如下说明:
项 说明 基本信息汇总 因变量Y(标签项)分类数据分布情况等 训练集或测试集模型评估结果 分析训练集和测试集数据的模型效果评估,非常重要 测试集结果混淆矩阵 测试集数据的进一步效果评估,非常重要 模型汇总表 模型参数及评估汇总表格 模型代码 模型构建的核心python代码 上述表格中,基本信息汇总表格展示因变量Y的分类数据分布情况,接着展示训练集和测试集效果情况,并且单独提供测试集数据混淆判断矩阵,进一步分析测试数据的正确效果等,模型汇总表格展示整体模型参数情况,并且提供sklean进行朴素贝叶斯模型构建的核心代码。
-
5、文字分析
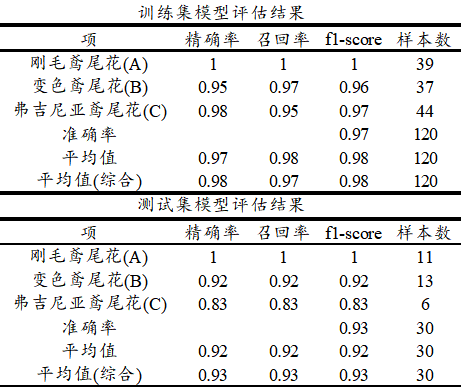
上表格中分别针对训练集和测试集,提供四个评估指标,分别是精确率、召回率、f1-scrore、准确率,以及平均指标和样本量指标等,如下表格说明:
项 说明 精确率 比如:预测为A类时,事实上是A类的比例,越大越好 召回率 比如:事实上是A类时,预测为A类的比例,越大越好 F1-score 精确率和召回率的调和平均数,越大越好,一般使用此指标较多 准确率 整体上全部数据预测准确的比例情况,越大越好,仅1个数字 平均值 对应指标的平均值,越大越好 平均值(综合) 对应指标的加权平均值(考虑样本量情况下) 样本量 各类别的样本量情况 一般来说,f1-score指标值最适合,因为其综合精确率和召回率两个指标,并且可查看其平均值(综合)指标,本案例为0.98,并且测试数据的表现上为0.93,意味着评估效果良好。
进一步地,可查看测试数据的‘混淆矩阵’,即模型预测和事实情况的交叉集合,如下图:
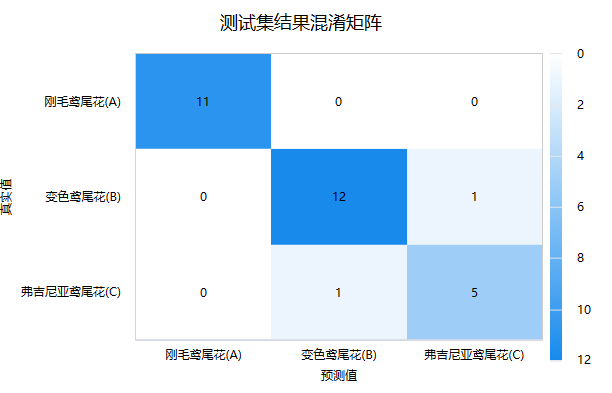
‘混淆矩阵’时,右下三角对角线的值越大越好,其表示预测值和真实值完全一致。本测试数据中有2个样本被判断类别出错,整体模型较优。
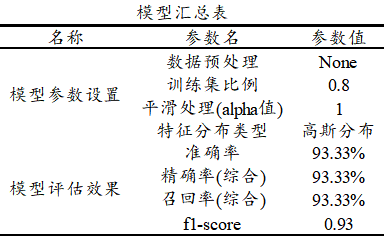
最后针对模型汇总表,其展示构建朴素贝叶斯模型各项参数设置,上表格中单独有输出平滑处理alpha值,当alpha=1.0时,称作Laplace平滑,当0
model = GaussianNB(alpha=1.0)
model.fit(x_train, y_train)
-
6、剖析
涉及以下几个关键点,分别如下:
-
朴素贝叶斯模型时是否需要标准化处理?
-
朴素贝叶斯模型时,其并不涉及距离等计算,不关注于数据的量纲情况,而只关注于各数据情况下的概率情况,因而通常不需要做任何处理。
-
训练集比例应该选择多少?
-
如果数据量很大,比如1万,那么训练集比例可以较高比如0.9,如果数据量较小,此时训练集比例选择较小预留出较多数据进行测试即可。
-
保存预测值
-
保存预测值时,SPSSAU会新生成一个标题用于存储模型预测的类别信息,其数字的意义与模型中标签项(因变量Y)的数字保持一致意义。
-
疑难解惑
-
SPSSAU机器学习如何进行预测?
-
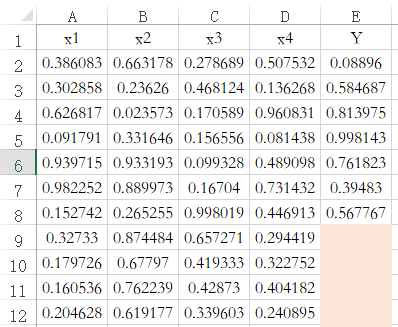
SPSSAU中默认带有数据预测功能,当特征项X有完整数据,但标签项(因变量Y)没有数据时,此时‘保存预测值’,SPSSAU会默认对此种情况进行预测。如下图中的编号9到12共4行数据,其只有X没有Y,那么保存预测值时,默认对该4行数据进行预测。机器学习的各方法(包括决策树/随机森林/KNN/贝叶斯/支持向量机和神经网络等)均遵从此规则。
-
SPSSAU机器学习中量纲归一化处理的具体规则情况?
-
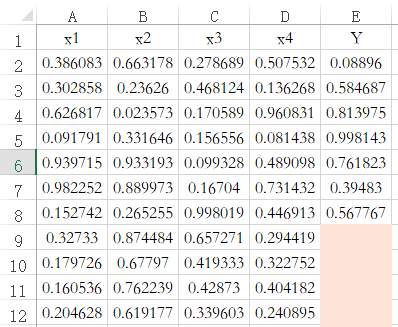
SPSSAU中,机器学习时均具有归一化参数值,并提供正态标准化/区间化/归一化等方式。其原理是针对具有完整数据的特征项X分别进行处理。比如下图中是针对编号为2~12共计11项的4个X分别进行处理。
-
机器学习中分类任务和回归任务的区别是什么?
-
机器学习包括分类任务和回归任务,当标签项(因变量Y)为类别数据时,其为分类任务,比如研究X对于“贷款是否逾期”的预测作用,“是否逾期”这个分类数据,因而此时此为分类任务。如果因变量Y为定量数据,比如研究X对于“贷款金额”的预测作用,“贷款金额”为定量数据,因而为回归任务。决策树/随机森林/支持向量机和神经网络等时,SPSSAU默认会对因变量Y进行识别,并且自动选择分类任务或者回归任务。当然研究者可以在“更多参数设置”处进行选择设置。另外,KNN和贝叶斯这两项仅提供分类任务。
-
机器学习时提示‘分类数据必须为整数’?
-
机器学习包括分类任务和回归任务,如果是定量数据Y进行分类任务,此时系统会提示“分类数据必须为整数”。决策树/随机森林/支持向量机和神经网络等时,可通过“更多参数设置”处进行选择设置,以及KNN和贝叶斯这两项仅提供分类任务。
-
机器学习算法时保存数据集标识的意思是什么?
-
选择‘保存数据集标识’后,SPSSAU会新生成一个标题,用于标识模型构建时训练集或测试集,使用数字1表示训练集,数字2表示测试集。如果后续分析时(比如绘制ROC曲线)只针对训练集,那么使用筛选样本功能,筛选出训练集后分析即可。
-
如何将多个机器学习模型数据绘制ROC曲线?
-
如果有多个机器学习模型后,需要对比模型优劣情况。建议按下述步骤进行。
-
第1步:每个机器学习模型最后一次构建后,选中‘保存预测信息’,系统会生成类别的预测概率;
-
第2步:将多个机器学习模型的某类别的预测概率值一并纳入作为X,以及将Y作为Y,进行ROC曲线【注意,放入的是某个类别的预测概率值】;
-
第3步:设置ROC曲线时对应的分割点,需要注意的是,分割点一定要设置为放入的对应类别时预测概率值对应的数字。
-
需要提示的是:预测概率是指某类别的预测概率值,二分类时只有两个数字,比如是和否(数字1和数字0表示),那么‘是’对应的预测概率值即为模型预测出‘是’的概率,‘是’和‘否’的概率加和一定为1。
-
机器学习算法中保存预测信息具体是什么意思?
-
如果选中保存预测信息,并且为分类任务时,SPSSAU会新生成两项标题,分别是预测类别和预测概率。预测类别是指最终预测出来Y的类别,预测概率是指预测出Y的每个类别对应的概率情况;事实上某个类别的预测概率相对最大时,此时预测类别就为该类别(比如Y有A/B/C共3个类别,某样本时3个类别的预测概率分别是0.4,0.5,0.1),那么预测类别则为B类别。
-
预测类别标题名称类似为‘NeutralNetwork_Prediction_****’,以及预测属于每个类别概率标题名类似‘NeutralNetwork_Prediction_probability_****’。
-
保存预测信息后,可进一步使用预测概率进行其它的分析或者处理,比如绘制ROC曲线等。