冗余分析(Redundancy Analysis, RDA)是一种约束排序方法,用于分析响应变量矩阵(Y)与解释变量矩阵(X)之间的关系。RDA结合了多元回归分析和主成分分析(PCA)的优点,通过构建线性模型来解释响应变量的变异,并将这些变异分解为可由解释变量解释的部分(约束变异)和不可解释的部分(非约束变异)。
RDA的数学模型可以表示为:Y = XB + E
其中:
-
Y 是响应变量矩阵(n×m,n为样点数,m为响应变量数)
-
X 是解释变量矩阵(n×p,n为样点数,p为解释变量数)
-
B 是回归系数矩阵(p×m)
-
E 是残差矩阵(n×m)
RDA首先对响应变量矩阵Y进行多元线性回归,得到由解释变量X预测的Y值矩阵,然后对预测值矩阵进行主成分分析,提取主要的排序轴。这样,RDA轴既反映了响应变量间的关系,又体现了环境变量对响应变量的影响。
-
RDA广泛应用于生态学、环境科学等领域,特别适用于:
-
1.分析环境因子对物种群落结构的影响
-
2.识别影响生态系统的主要环境驱动因子
-
3.探索多变量数据集之间的关系
-
4.进行群落生态学研究
冗余分析案例
-
1、背景
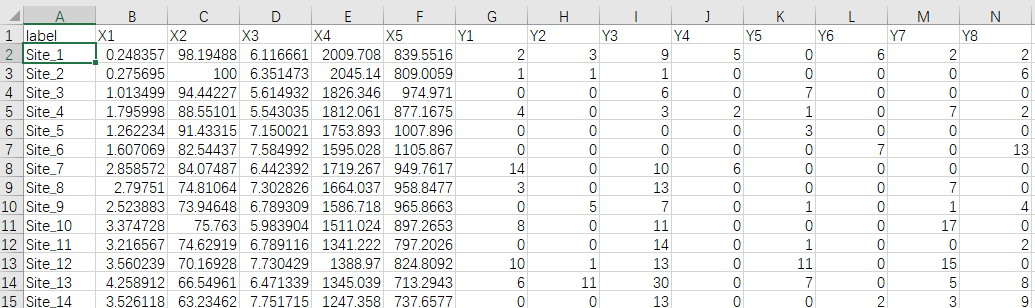
某生态研究团队调查了30个不同地点的植被群落和环境因子,希望通过RDA分析了解环境因子如何影响植物群落的分布格局。数据包括5个环境变量(X1-X5)和8个植物物种(Y1-Y8),部分数据如下。
-
2、理论
RDA的数学原理如下:
1.数据预处理:对数据进行中心化或标准化处理,SPSSAU默认提供‘标准化’参数,研究者可不勾选该参数,此时SPSSAU则进行中心化处理;
2.多元回归:将响应变量(Y)对解释变量(X)进行多元回归,得到拟合值矩阵
3.特征值分解:对拟合值矩阵进行奇异值分解(SVD),提取RDA轴
4.方差分解:将总方差分解为约束方差(可由环境变量解释)和非约束方差(残差)
5.显著性检验:通过置换检验判断环境变量对响应变量的解释是否显著
RDA的排序结果可以用双序图(biplot)展示,图中同时显示样点、响应变量和解释变量的位置关系:
-
样点之间的距离反映群落组成的相似性
-
响应变量箭头的长度反映其在排序中的重要性
-
解释变量箭头的方向反映其与排序轴的关系
-
样点与解释变量箭头的夹角反映环境偏好
-
-
3、操作
本案例操作截图和说明分别如下:
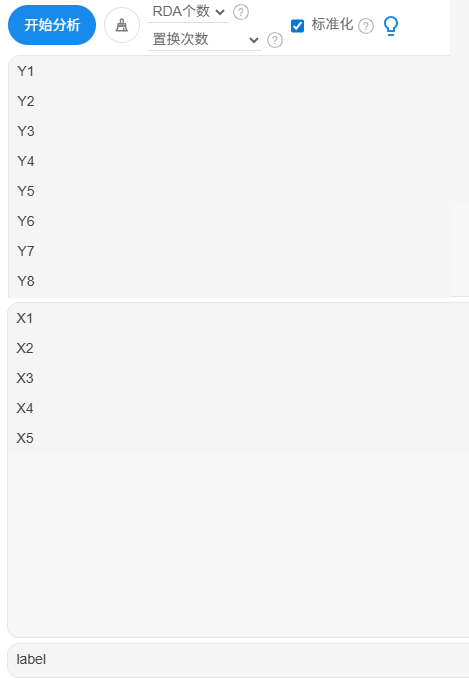
将X和Y分别放入右侧框中,右下方放入样本点的标签列数据,如果不放入,SPSSAU默认会输出比如第1项,第2项等内容。以及RDA个数默认是3个。
SPSSAU进行RDA分析时,共涉及3个参数,分别是RDA个数,标准化和置换次数,如下述:
-
关于‘RDA个数’
-
SPSSAU默认是3个,研究者可自行设置RDA个数,但需要注意的是,RDA个数需要小于X或Y的个数,且需要小于样本点的个数。
-
关于‘标准化’
-
默认SPSSAU选中该参数,其处理量纲问题,将X和Y均进行标准化处理。如果不选中,默认SPSSAU则进行中心化处理。
-
关于‘置换次数’
-
默认为200,更多次数结果更稳定但计算时间更长。
-
-
4、SPSSAU输出结果
SPSSAU中进行冗余分析时,其共输出9个表格和RDA双序图,分别说明如下:
项 名称 说明 1 置换检验结果表(方差分析表) 显示模型整体显著性检验结果 2 方差分解结果 显示总方差、约束方差和非约束方差及其比例 3 特征值和解释方差 显示各RDA轴的特征值和解释方差比例 4 RDA双序图 可视化展示样点、响应变量和解释变量的关系 5 解释变量与RDA相关性及解释方差 显示各解释变量的解释方差百分比及与RDA轴的相关性 6 解释变量与响应变量相关性 显示解释变量与响应变量间的相关性 7 样本得分表 显示各样点在各RDA轴上的坐标 8 Y变量得分表 显示各响应变量在各RDA轴上的坐标 9 X变量得分表 显示各解释变量在各RDA轴上的坐标 10 样本缺失情况汇总 展示真实进入算法模型时有效样本和排除在外的无效样本情况等 -
提示:
-
通常分析上,首先查看‘门槛模型检验’,用于判断模型是否有着‘门槛效应’,只有模型有着门槛效应后才能进一步分析,否则应该使用普通回归模型比如OLS回归等。
-
如果分析目的是多次对比各种门槛模型,那应该更多关于‘门槛模型比较’这个表格,其用于展示模型质量指标,包括RSS、MSE、R方、AIC和BIC等,RSS和MSE均为越小越好,R方一般越大越好,AIC和BIC这两个指标用于对比不同模型的优劣,该两个指标均为数值越小,模型越优,以及该两个指标相对更倾向于选择更简约的模型。
-
-
5、文字分析

模型解释的方差为1.394,占总方差的17.4%,说明解释力偏弱。F 值为1.013,p 值为0.490,远大于0.05,表示模型整体不显著。原假设为“X对Y无显著解释力”,此结果无法拒绝原假设。也即说明当前模型其实无法使用,但出于案例演示需要,继续进一步往下解读各表格。
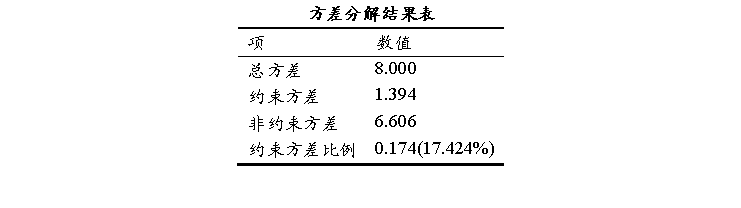
上表格中,总方差(Total Variance),其表示Y变量变异性的总和,反映了数据集的整体变异性;约束方差(Constrained Variance),其表示由X变量解释的响应变量变异部分,表示X对Y的影响程度;非约束方差(Unconstrained Variance),其表示未被X变量解释的变异部分,可能由随机因素或其他未测量因素引起;约束方差比例,其表示X变量对于Y的解释力度,该比例越高,说明X对Y的解释能力越强,模型的拟合度越好。
表格中显示约束方差比例仅17.424%,即说明X对Y的解释能力一般,这也与置换检验结果为没有显著性对应。
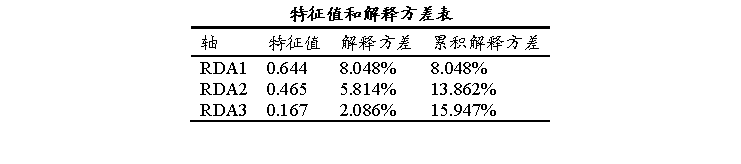
本次分析时共设置3个RDA,RDA1是最重要的轴,解释了 8.05% 的变异。前三轴累计解释仅 15.95%,说明数据维度分散,主轴解释力有限。
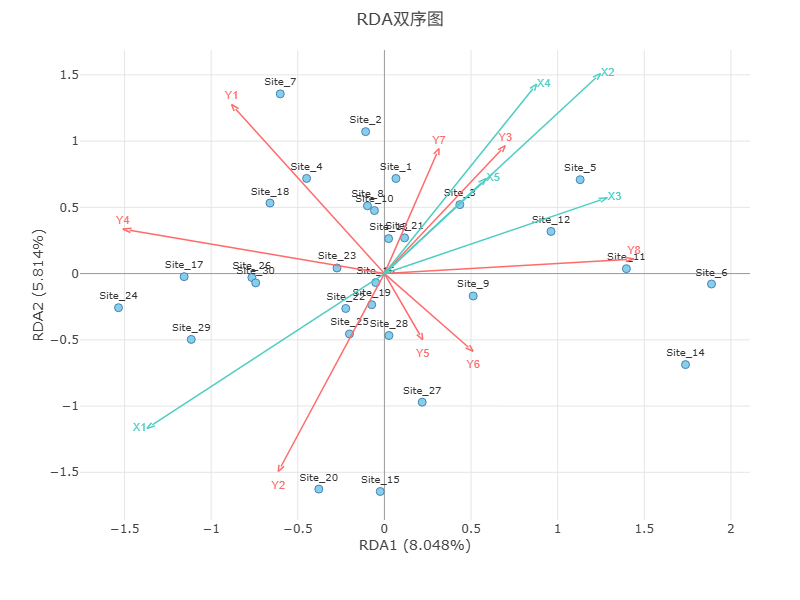
RDA双序图是最重要结果;分析解读可参考下述:
第一:可通过样点位置、箭头长度和方向,一图看清‘谁和谁相似’、‘什么因素重要’、‘谁受什么影响’等;
第二:任意两样点挨的越近,则意味着该两样点越‘相似’;
第三:箭头越长则意味着该变量的重要性越高(不论X变量或Y变量);
第四:样本点离某变量箭头越近,意味着该样本点与该变量之间的关系越强;
第五:X变量和Y变量之间的夹角表示二者关系强度,如果二者是垂直90度则说明二者没有关系,越接近0度意味着二者越强的正相关关系,越接近180度说明越强的负相关关系。
-
提示:可点击‘隐藏样点’将图中的样本点隐藏起来;除此之外,可切换RDA下拉框展示不同的RDA轴时,X与Y在RDA轴上的映射关系。
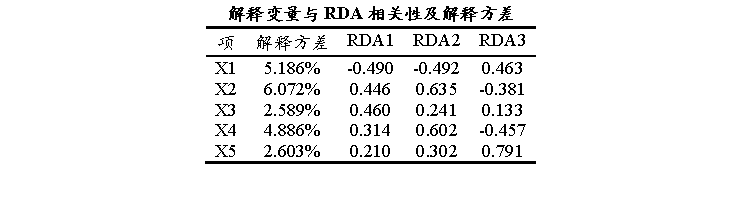
上表格展示X变量的重要性情况;解释方差指标:其指某个X变量能够解释所有Y变量总变异的百分比,该值越大意味着该X是主要的驱动因子;解释方差= 单个X变量通过回归能预测的所有Y变量方差 ÷ Y变量总方差 × 100%,其实际意义为该X变量单独能解释多少比例的Y变量变化;X变量与RDA轴的相关性系数,该系数表示X变量与RDA轴的关系情况,该指标值较高时则意味着该X变量在该轴上的作用越大,可以辅助理解X对Y变异的具体贡献。
上表格可以看到:X2是最强解释变量,但也仅6.072%,在RDA1和RDA2上贡献显著。X1、X4也有较高解释力,X3、X5较弱。相关系数显示变量在不同轴上的方向和强度。
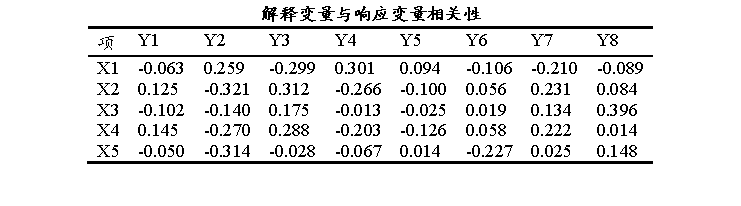
上表格展示X变量和Y变量的相关关系情况;分析上可以理解为X和Y的Pearson相关系数情况;可识别出强相关关系,绝对值较大的相关系数(如>0.5或< -0.5)表示强相关关系,可辅助分析哪些X对Y有重要关系。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
SPSSAU中RDA分析时如何标准化处理?
-
SPSSAU默认提供标准化处理,如果不选中该参数,则进行中心化处理。
-
SPSSAU中RDA分析时显著性检验?
-
RDA分析时,其通过置换检验判断环境变量的解释能力是否显著,默认置换次数是200次。
-