1、背景

本案例研究身体特征指标（共3个X，分别是体重X1、腰围X2和脉博X3）对于训练指标（共3个Y，分别是单杠Y1、弯曲Y2和跳高Y3）的影响关系，样本数据为20个。由于数据样本量非常小（20个），并且因变量为3个无法概括成一个，并且3个X之有着共线性，因此使用PLS回归进行研究。

2、理论

PLS回归的核心思路是：将X和Y进行信息浓缩，得到主成分，然后通过研究主成分与X或Y之间的关系，从而研究得到X对于Y的影响关系。PLS回归融合了主成分分析、典型相关和多元线性回归共三个算法的内容，主成分用于信息浓缩，典型相关用于研究多个X和多个Y之间的关系，多元线性回归用于研究影响关系情况。

3、操作

本例子研究3个X对于3个Y的影响关系，操作截图如下：

首先第一步成分数量这里不选择，默认即可，SPSSAU会自动生成主成分数量，经过对交叉有效性和投影重要性VIP分析，确认好主成分数量之后；接着第二步操作，在这里选择主成分数量，即得到最终结果。

主成分数量的选择判断上，可综合使用多个指标进行分析综合进行判断，包括‘交叉有效性’，‘VIP值’，‘精度分析’，‘RMSEP值变化’，‘R 方值变化’等5个角度进行判断和决策。下面以‘VIP值’，‘交叉有效性’和‘RMSEP值变化’这三项进行本次案例的主成分个数判断

>

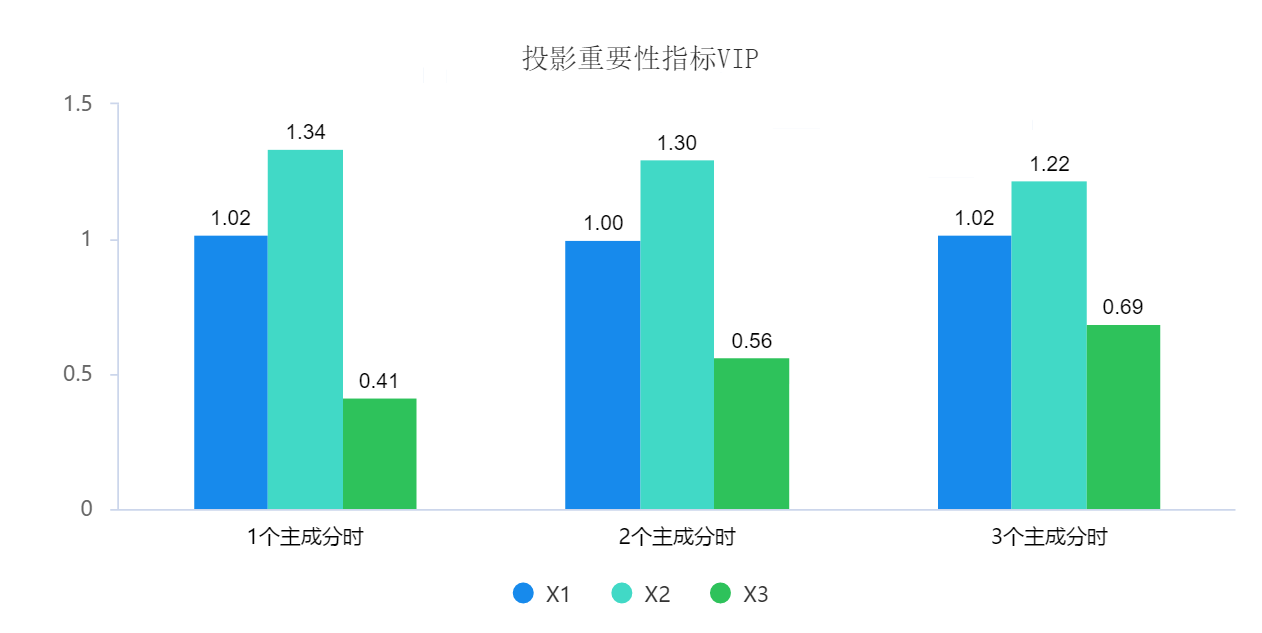
投影重要性VIP指标，其反映了X对于Y（所有）的解释力度，并且区分不同主成分的情况，如果说主成分继续增加，VIP指标并没有明显的增加时，则说明找出最佳的主成分数量。上表和下图显示，1个主成分和2个主成分时，3个X对应的VIP指标变化均很小，仅X3有着一定变化（从0.414到0.565），2个主成分到3个主成分时，3个X对应的VIP指标变化也很小。因而说明可能1个主成分或者2个主成分均较为适合，具体还可以结合交叉有效性进行综合决定。

另外从下图还可以看到，X2对于Y的影响力度最高，其次是X1，X3对于Y的影响力度最小。

交叉有效性中包括不同主成分数量时（上表分别是1个主成分，2个主成分和3个主成分）时，误差平方和SS，预测误差平方和PRESS，以及Qh2共三个指标。SS和PRESS为中间过程值，Qh2 = 1 – PRESSh/SS(h-1)；比如h=2(即2个主成分时)，Qh2 = 1 - 135933.273/96596.314 = -0.407。当h=1时，Qh2为1。

至于如何利用交叉有效性确认主成分数量，常见的标准是Qh2>=(1-0.95)^2=0.0975时，说明该主成分对模型是有贡献的，如果Qh2小于0.0975，意味着该成分对于模型没有贡献，上表格中，成分数量为2或者3时，Qh2均小于0.0975，因此说明选择2个或者3个主成分不合适，因此第2个或者第3个主成分对于模型没有贡献，因此最终选择1个主成分作为结论。

除此之外，可结合RMSEP（预测误差均方根）值查看，该值意义为‘平均的残差值’，该值肯定是希望越小越好，如果说主成分个数增加，但是该值变化不明显，那就说明找到对应的最佳主成分。本次分析时，如下图所示，

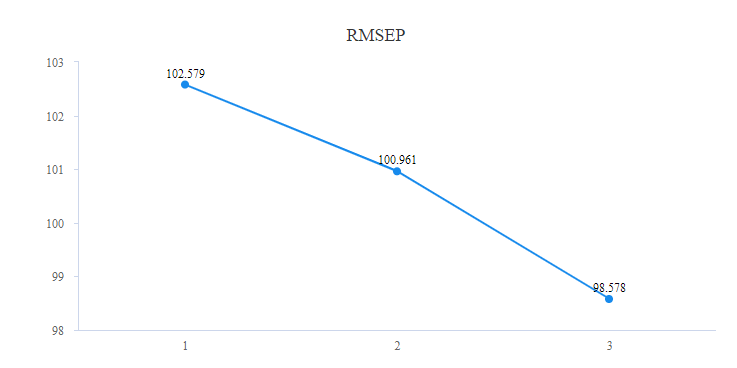
如果提取为1个主成分，此时RMSEP值为102.579，2个主成分时为100.961，3个主成分时为98.578，RMSEP值变化非常不明显，意味着提供1个或者2个均可，最终考虑提供1个主成分作为结论。

上述投影重要性VIP分析，交叉有效性和RMSEP值分析结束后，最终确认主成分数量为1，接着选择主成分数量为1进行PLS回归分析。

特别提示

• 主成分数量如果为1个，则说明X全部浓缩成1个整体特征，此种情况下在实际研究中出现较少。

4、SPSSAU 输出结果

SPSSAU共输出9个表格和1个图形，分别如下表：

5、文字分析

最终提取主成分数量为1个，分别命名为U1和V1，U1对应着X的信息提取主成分，V1对应着Y的信息提取主成分。主成分U与自变量X之间的关系表达式，以及主成分V与因变量Y之间的关系表达式 ，如下所示：

• 主成分U1=0.590*X1+0.771*X2-0.239*X3

• 主成分V1=-1.101*Y1-1.341*Y2-0.461*Y3

Loading值表达主成分与研究项的相关关系情况，该值介于-1~1之间，绝对值越大说明相关关系越强，正负号表示相关关系方向。从上表格可以看到：主成分U1分别与X1,X2均有着较强的正相关关系，loading值分别是0.666和0.676，主成分U1与X3有着负向相关关系。

主成分V1与Y1,Y2,Y3均有着负向相关关系，loading值全部均小于0。结合loading值，研究人员可对主成分U1或V1进行命名，让其具有实际意义，而非仅仅是个符号。

上表格展示因变量Y与自变量X之间的回归关系表达式，包括每个因变量Y与所有自变量间的关系表达式，如下所示：

• Y1=-0.202*X1-0.264*X2+0.082*X3

• Y2=-0.245*X1-0.321*X2+0.099*X3

• Y3=-0.084*X1-0.110*X2+0.034*X3

上表格显示，X1,X2对于Y1，Y2和Y3均为负向影响，X3对于Y1，Y2和Y3均为正向影响，至于影响大小幅度情况，可结合图形和表格数字进行描述，建议研究人员可结合图形进行研究X对于Y的影响幅度情况。

精度分析研究主成分对于研究项的信息提取情况，并且分为两个，分别是主成分U与X或Y的精度分析；主成分V分别与X或Y的精度分析；但实际研究中，一般只需要分析主成分U与X的精度分析；主成分V与Y的精度分析。原因在于主成分U为X的信息浓缩，主成分V为Y的信息浓缩。

上表格显示，主成分U1对于所有3个X信息提取比例是0.695（方差解释率，即69.5%），提取信息较高。X1,X2的信息提取比例非常高（分别是0.898和0.925），但是主成分U1对于X3的信息提取比例较低为0.261，意味着主成分U1无法提取出X3的信息量。

上表格显示，主成分V1对于所有3个Y信息提取比例是0.735，提取信息比例高。主成分V1对于3个Y都有着较高的信息提取，分别是0.775，0.883和0.549。

投影重要性指标VIP可用于辅助判断主成分数量，并且更多用于研究X对于Y（整体）的影响力度，从上表可知，X1对于所有Y的解释力度最高(VIP值为1.336)，其次是X1(VIP为1.022)，X3对于所有Y的解释力度最低。另外投影重要性指标VIP分析还可结合图形进行描述。

交叉有效性表格用于确认主成分数量，此处已经是主成分确认为1个时的结果，不在有意义。

模型R 方值表格，展示出所有X分别对于Y的解释力度，比如本次中，X1,X2和X3可以解释Y1，0.236即23.6%的变化原因。同时分别对于Y2和Y3的解释比例分别是35.1%和4.1%。

上表格展示回归系数的显著性，和普通的线性回归一样，分别时先查看p 值，如果p 值小于0.05，再接着查看回归系数的正负向。比如上表格中，X1对于Y2呈现出0.01水平的显著性（t =-3.772,p =0.001 <0.01)，回归系数值为-0.622<0，即说明X1对于Y2有显著的负向影响关系。

通常情况下，PLS回归时的X个数会非常多，因此表格信息会非常大，建议可汇总描述说明。

6、剖析