-
-
有时候,我们需要判断一些事情是否将要发生,是否愿意购买,候选人是否会当选等。
-
这类问题的特点是因变量(Y)是定类数据,并且只使用两个数字去表示,规定为 1和0,并且 只能是1或0,比如1代表愿意0代表不愿意;1代表会0代表不会;1代表可以0代表不可以;1代表喜欢0代表不喜欢。
-
如果想研究某些因素(X)对于因变量(Y)的影响关系,并且因变量(Y)只有两个取值时(并且 只能是0和1),此时则应该使用二元Logistic回归分析。
-
如果说Y对应的数字不为0和1;可以使用SPSSAU的‘ 数据编码’功能进行设置
-
-
SPSSAU分析结果表格示例如下:
二元Logit回归分析基本汇总 名称 选项 频数 百分比 汇总 有效 220 100% 缺失 0 0 总计 220 100% -
模型似然比检验结果 似然比卡方值 df p AIC 值 BIC 值 12.633 3 0.006 162.960 175.003 -
二元Logit回归分析结果汇总:
二元Logit回归分析结果汇总 项 回归系数 标准误差 z 值 p 值 OR值 95% CI(LL) 95% CI(UL) X1 1.001 2.282 3.457 0.000 2.722 0.448 1.555 X2 0.833 0.353 2.36 0.018 2.301 0.141 1.525 X3 -0.088 -0.292 -0.303 0.762 0.915 0.661 0.485 截距 -5.818 1.258 -4.528 0.000 0.003 -8.337 -3.3 因变量Y: Y McFadden R 方: 0.207 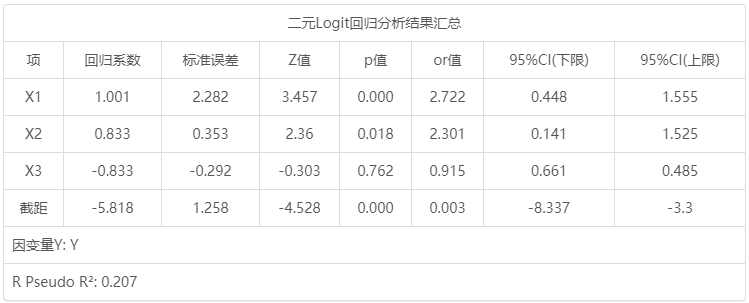
-
二元Logit回归预测准确率汇总:
二元Logit回归预测准确率汇总 预测值 预测准确率 预测错误率 0 1 真实值 0 14 38 26.92% 73.08% 1 16 162 96.43% 3.57% 汇总 80.00% 20.00%
二元Logit回归案例
-
1、背景
当前有一份数据是用来研究影响用户购买IPHONE X的因素,包括‘外观喜欢度’,‘性能情况’和‘品牌价值认可度’共3个潜在的影响因素;以及被影响项为‘是否购买IPHONE X’。由于Y为定类数据,并且只分为两项即购买和不购买,因而适用于二元Logit回归分析。
-
2、理论
二元Logit回归分析用于研究X对于Y的影响关系,其中X通常为定量数据(如果X为定类数据,一般需要做虚拟(哑)变量设置),Y为二分类定类数据(Y的数字一定只能为0和1)。二元Logit回归分析时,首先分析p 值,如果此值小于0.05,说明具有影响关系,接着再具体研究影响关系情况即可,比如是正向影响还是负向影响关系等;除此之外,还可以写出二元Logit回归分析的模型构建公式,以及模型的预测准确率情况等。
-
特别提示
-
一定注意,Y对应的数字一定只能为0和1;如果不是,可以使用‘数据编码’功能进行设置
-
如果X为定类数据,通常情况下需要将X进行虚拟(哑)变量设置【SPSSAU中生成变量功能中有】。
-
如果X为定类数据,此时可以考虑使用交叉卡方分析去研究X和Y的关系。
-
如果X非常多(比如超过10个),此时可以先对定类的X与Y进行卡方分析,对定量的X与Y进行方差分析(或t检验),先看有没有差异关系,将最终有差异关系的X放入二元Logit回归模型中,这样X会较少,并且X与Y均有差异关系,也更可能有影响关系,此时二元Logit回归模型的预测准确率会更高。
-
-
3、操作
本例子中研究X对于Y的差异;X分别为‘外观喜欢度’,‘性能情况’和‘品牌价值认可度’,Y为是否购买IPHONE X’。放置如下:
-
4、SPSSAU输出结果
二元Logit回归分析基本汇总 名称 选项 频数 百分比 汇总 有效 220 100% 缺失 0 0 总计 220 100% 第一个表格仅仅统计下分析的基本情况,分析的有效样本量情况,意义相对较小。
模型似然比检验结果 似然比卡方值 df p AIC 值 BIC 值 12.633 3 0.006 162.960 175.003 第二个表格为似然比检验,对p 值进行分析即可,如果该值小于0.05,则说明模型有效;反之则说明模型无效。AIC 值和BIC 值用于对比两个模型的优劣时使用,此两个值均为越小越好。
-
二元Logit回归分析结果汇总:
二元Logit回归分析结果汇总 项 回归系数 标准误差 z 值 p 值 OR值 95% CI(LL) 95% CI(UL) 外观喜欢度 1.001 2.282 3.457 0.000 2.722 0.448 1.555 性能情况 0.833 0.353 2.36 0.018 2.301 0.141 1.525 品牌价值认可度 -0.088 -0.292 -0.303 0.762 0.915 0.661 0.485 截距 -5.818 1.258 -4.528 0.000 0.003 -8.337 -3.3 因变量Y: 是否购买IPHONE X McFadden R 方: 0.207 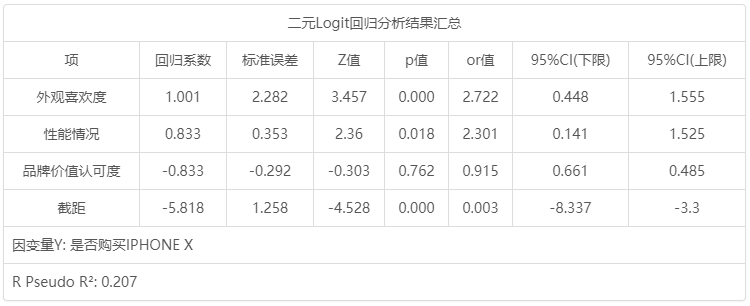
第三个表格用于研究X对于Y的影响关系情况,表格中有意义的指标信息包括:p 值,回归系数,OR值和R Pseudo R 2。其它指标包括标准误,z 值,95% CI值意义相对较小。
-
二元Logit回归预测准确率汇总:
二元Logit回归预测准确率汇总: 预测值 预测准确率 预测错误率 0 1 真实值 0 14 38 26.92% 73.08% 1 16 162 96.43% 3.57% 汇总 80.00% 20.00% 第四个表格输出模型的预测准确率情况,显示出Y本身为0,或者Y本身为1的前提下,的预测准确率或者预测错误率。以及最终整体的预测准确率和预测错误率等指标。
-
5、文字分析
二元Logit回归分析基本汇总 名称 选项 频数 百分比 汇总 有效 220 100% 缺失 0 0 总计 220 100% 将外观喜欢度, 性能情况, 品牌价值认可度共3项作为自变量,而将是否购买IPHONE X作为因变量进行二元Logit回归分析,从上表可以看出,总共有220个样本参加分析,并且没有缺失数据。
模型似然比检验结果 似然比卡方值 df p AIC 值 BIC 值 12.633 3 0.006 162.960 175.003 首先对模型进行似然比检验,从上表可知:此处模型检验的原定假设为:是否放入自变量(外观喜欢度, 性能情况, 品牌价值认可度共3项)两种情况时模型质量均一样;这里p 值小于0.05,因而说明拒绝原定假设,即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。
-
二元Logit回归分析结果汇总:
二元Logit回归分析结果汇总 项 回归系数 标准误差 z 值 p 值 OR值 95% CI(LL) 95% CI(UL) 外观喜欢度 1.001 2.282 3.457 0.000 2.722 0.448 1.555 性能情况 0.833 0.353 2.36 0.018 2.301 0.141 1.525 品牌价值认可度 -0.088 -0.292 -0.303 0.762 0.915 0.661 0.485 截距 -5.818 1.258 -4.528 0.000 0.003 -8.337 -3.3 因变量Y: 是否购买IPHONE X McFadden R 方: 0.207 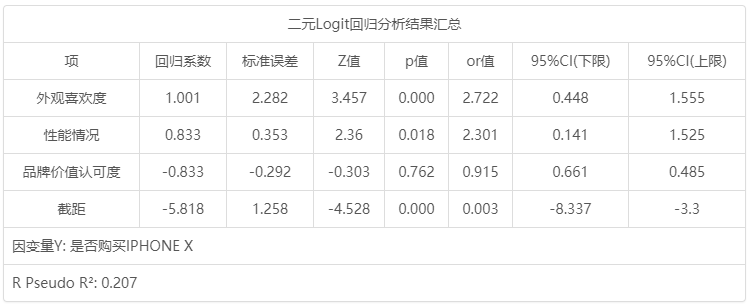
-
从上表可知
-
将外观喜欢度, 性能情况, 品牌价值认可度共3项为自变量,而将是否购买IPHONE X作为因变量进行二元Logit回归分析,从上表可以看出,模型伪R 2值(Pseudo R 2)为0.207,意味着外观喜欢度, 性能情况, 品牌价值认可度可以解释是否购买IPHONE X的20.7%变化原因。从上表可知:模型公式为:ln(p /1-p )=-5.818 + 1.001*外观喜欢度 + 0.833*性能情况-0.088*品牌价值认可度(其中p 代表是否购买IPHONE X为1 的概率,1-p 代表是否购买IPHONE X为0的概率)。最终具体分析可知:
-
外观喜欢度的回归系数值为1.001,并且呈现出0.01水平的显著性(p =0.000 <0.01),意味着外观喜欢度会对是否购买IPHONE X产生显著的正向影响关系。以及优势比(OR值)为2.722,意味着外观喜欢度增加一个单位时,Y的变化(增加)幅度为2.722倍。性能情况的回归系数值为0.833,并且呈现出0.05水平的显著性( p =0.018<0.05),意味着性能情况会对是否购买IPHONE X产生显著的正向影响关系。以及优势比(OR值)为2.301,意味着性能情况增加一个单位时,购买IPHONE X意愿幅度增加2.301倍。品牌价值认可度的回归系数值为-0.088,但是并没有呈现出显著性(p =0.762> 0.05),意味着品牌价值认可度并不会对是否购买IPHONE X产生影响关系。
总结分析可知:外观喜欢度, 性能情况共2项会对是否购买IPHONE X产生显著的正向影响关系。但是品牌价值认可度并不会对是否购买IPHONE X产生影响关系。
-
-
二元Logit回归预测准确率汇总:
二元Logit回归预测准确率汇总: 预测值 预测准确率 预测错误率 0 1 真实值 0 14 38 26.92% 73.08% 1 16 162 96.43% 3.57% 汇总 80.00% 20.00% 通过模型预测准确率去判断模型拟合质量,从上表可知:研究模型的整体预测准确率为80.00%,模型拟合情况比较糟糕。当真实值为0(不购买)时,预测错误率为73.08%;另外当真实值为1(购买)时,预测错误率为3.57%。
-
特别提示
-
当前数据为测试数据预测准确率较低,如果实际研究中,数据预测准确率很低,比如低于85%,此时可以考虑删除部分X,也或者对X进行一些数据编码组合处理,多次进行二元Logit回归分析进行对比结果,选出最优的模型结果。
-
-
6、剖析
二元Logit回归分析涉及以下几个关键点,分别如下:
-
特别提示
-
Y对应的数字一定只能为0和1;如果不是,可以使用‘数据编码’功能设置;
-
如果模型预测准确率较低,需要多次进行分析对比,找出最优的模型结果;
-
如果X是定类数据,此时需要对X进行虚拟(哑)变量设置。
-
如果X的个数非常多(比如超过10个),此时需要进行甄别选择出有意义的X(比如使用方差分析或者卡方分析,选出X与Y有显著差异的X放入二元logit回归模型中)。
-
疑难解惑
-
提示“出现奇异矩阵”
-
出现奇异矩阵,有两种可能的问题。一是有虚拟(哑)变量出错(需要少放一项);二是某个数字完全恒定。
-
关于虚拟(哑)变量(需要少放一项): https://www.spssau.com/helps/otherdocuments/dummy.html
-
关于某个数字完全恒定:即某分析项只有1个数字,可使用频数分析进行检查后将该项从模型中移除出去。
-
提示“Y值恒定”
-
如果提示“Y值恒定”,则说明因变量Y全部为一个数字(0或者1),可使用频数分析进行检查。同时需要使用“数据处理->数据编码”功能进行处理设置。
-
提示‘数据质量异常’
-
如果出现数据质量异常提示,通常是由于以下原因所致,可逐一进行检查:
-
第一:样本量非常少,如果样本量太少(比如10个)很可能出现此提示,建议加大样本量;
-
第二:自变量之间相关性非常强,建议使用【通用方法->相关分析】进行检验自变量之间的相关性,如果某两项之间的相关性高于0.7则说明相关性过高,建议删除部分项后再次进行分析。
-
提示“Y值只能为0或1”
-
二元Logit回归要求因变量Y只能包括数字0和1,而且不能全部为0或1;如果出现此提示则说明因变量有问题。可通过频数分析进行检查查看。同时,如果要对数字编码,则需要使用【数据处理->数据编码】功能,类似如下图(最终保证因变量Y只能有数字0和1):
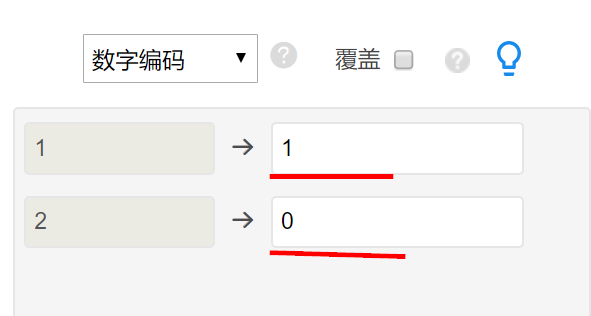
-
McFadden R 方、Cox & Snell R 方和Nagelkerke R 方相关问题?
-
Logit回归时会提供此3个R 方值,此3个R 方均为伪R 方值(并非像线性回归的R 方值意义一样),其值越大越好,但其无法非常有效的表达模型的拟合程度,意义相对交小,而且多数情况此3个指标值均会特别小,研究人员不用过分关注于此3个指标值。
-
‘Hosmer-Lemeshow拟合度检验’问题
-
Hosmer-Lemeshow检验(HL检验)为模型拟合指标,其原理在于判断预测值与真实值之间的gap情况,如果p值大于0.05,则说明通过HL检验,即说明预测值与真实值之间并无非常明显的差异。反之如果p值小于0.05,则说明没有通过HL检验,预测值与真实值之间有着明显的差异,即说明模型拟合度较差。
-
SPSSAU计算的HL检验与R软件、Stata软件等保持一致,但与IBM SPSS软件的结果有一定出入,这是由于边界问题的处理方式不一致。
-
二元logit回归提示数据质量异常?
-
如果出现此提示,建议按以下步骤进行检验。
-
第一:将所有分析项(X和Y全部一起)做相关分析,查看是否有相关系数非常低或者非常高的项;如果非常低(比如小于0.1)说明完全没有关联关系,非常高(比如大于0.8)说明共线性问题严重,将此类自变量移除出去,再次分析就好;
-
第二:检查因变量Y的分布情况,因变量Y仅仅两个数字0和1,如果分布严重不均匀(比如100个样本中仅5个样本为0,95个为1),有可能出现模型无法收敛最后无法输出结果;
-
第三:自变量中放入虚拟变量,比如学历有5项,虚拟变量出来为5项,5项全部都放入了模型,这一定会出错;
-
第四:分析样本量过小,比如分析项有10个,但分析样本量仅20个。
-
二元Logit回归中分类数据是否需要自己做虚拟变量处理?
-
如果自变量中有定类数据,此时需要做虚拟变量处理,具体可参考页面: https://www.spssau.com/helps/otherdocuments/dummy.html
-
z 值的意义是什么?
-
z 值=回归系数/标准误,该值为中间过程值无意义,只需要看p 值即可。有的软件会提供wald值(但不提供z 值,该值也无实际意义),wald值= z 值的平方。
-
crude OR和adjusted OR值?
-
在SPSSAU中进行二元Logit回归,如果放入一个X,得到的OR值即为crude OR,如果放入该X的时候还放入其余的控制项,并且得到对应该X的OR值,就称为adjusted OR值。
-
SPSSAU进行二元Logit回归时多少样本量适合?
-
在进行二元logistic回归时,样本量规则建议如下:因变量Y即01变量时,类别较少那项,比如1出现70,0出现30,以30为准,30/10=3(即类别频数较少项的频数除以10),则最多3个自变量X。
-
如果X的个数为10个,那么10*10=100,那Y的两个类别的较小频数最少为100。
-
二元Logit回归时结果显示各分组项?
-
如果是定类数据,可先对其进行虚拟(哑)变量设置,设置后再将具体分组项放入模型中即可,涉及虚拟(哑)变量原理说明,可点击查看。
-
SPSSAU进行二元logit回归的分析方式?
-
SPSSAU进行二元logit回归时,如果需要自动寻找显著的X,共提供3种方式,wald p 值逐步stepwise法,可选为向前wald p 值forward法和wald p 值向后backward法。一般情况下使用Stepwise法最多。
-
SPSSAU边际效应的使用?
-
SPSSAU进行二元logistic回归时,默认提供overall状态下的边际效应值(即观察点平均效应)。
-
Hosmer和Lemeshow检验(HL检验)过程表格解读?
-
SPSSAU默认输出HL检验结果及其中间过程表格,其检验原理上为将预测概率值按10分位数分为10个组别,然后计算每个组别的观测值和预测值,进而得到检验结果。HL检验过程表格可用于直观查看二元logit模型的拟合一致性(校准度)情况。除使用表格直观查看一致性情况,也可将‘HL检验结果表格’结果进一步用于绘制比如散点图或柱形图或折线图等,图示化展示模型的预测一致性情况。
-
二元logistic回归进行共线性诊断?
-
SPSSAU中二元logistic回归可进行共线性诊断,其原理是利用线性回归进行分析并且输出VIF值指标,使用VIF值指标进行判断,当VIF值小于10时认为共线性问题很弱可以接受,如果VIF值小于5则说明完全无线性问题,当VIF值大于10时需要移除该分析项(或者其它处理办法等)。
-
二元logistic回归逐步回归中间过程值?
-
如果进行逐步回归(包括向前法/向后法等),SPSSAU会输出其中间具体的迭代过程结果,便于分析人员查看X的进入或者移出模型具体过程信息,进一步深入分析等。
-
二元logistic回归进行交互项设置?
-
交互项是指比如X和Y的乘积项,可使用SPSSAU数据处理-》生成变量功能进行处理即可。
-
二元logistic回归时输出OR值非常大?
-
OR值为回归系数的指数次方,如果回归系数很大则OR值则会非常大。回归系数很大的原因是分析项的单位不统一,建议可对自变量X进行一些处理,比如取其对数值,或者标准化处理后再进行分析,需要提示的是处理后的数据进行分析,回归系数及其显著性一定会变化,此是正常现象。
-
p for trend这个指标如何计算?
-
p for trend指标是指某个X对于Y的影响时的趋势情况如何。实际研究中计算该指标,其步骤如下:
-
第1步:对X进行分组处理得到新的标题Xnew,比如预期将血压分为低、中和高共三组:
-
第2步:对Xnew中的组别赋值编码数字,比如低赋值编码为0,中为1,高为2(此种方式为常见的编码方式,当然也可使用低/中/高组分别的中位数作为赋值编码数字);
-
第3步:将Xnew纳入模型中,其对应得到p值即为p for trend指标。
-
原理上:即将X分成几个组别,并且用不同的数字标识出各个组别的相对大小后得到分组后的Xnew,这样Xnew只包括几个数字且数字代表各个等级组别,此时将Xnew纳入模型时,其得到的p 值即为p for trend。
-
另提示:将X进行分组和编码,建议可使用SPSSAU数据处理-》数据编码功能实现,也或者在EXCEL中处理。
