正态分布图(也称高斯分布图)是由德国的数学家和天文学家Moivre于1733年首次提出。从理论上讲,生活中绝大多数数据均满足正态分布,比如身高,体重,人的智商等等数据。而且当前的多数研究方法均默认假定数据呈现出正态分布。直方图用于直观展示数据特征情况,观察数据的正态分布特性,检验数据是否满足分析方法的前提(正态性)
-
特别提示
-
正态性是绝大多数研究方法的默认前提条件,但现实中由于数据量较少,因而很难呈现出完美的正态性;若直方图基本上呈现出正态性(钟形)即可,不用过多纠结数据的正态性。
-
通常情况下,直方图更适用于定量数据的检测。当然定类数据也适用。
-
直方图的常见使用场景如下:
-
相关分析时,数据的正态性查看(如果正态,则使用Pearson相关系数,反之如果数据分布明显不正态,则使用Spearman相关系数);
-
回归分析后模型检验,将残差进行正态性检验,如果残差呈现出正态性意味着模型构建良好,反之说明模型构建较差。
-
方差分析前,定量数据Y的正态性查看(此方法使用较少),如果不满足正态性则使用非参数检验。
-
其它(理论上讲,t 检验,单样本t 检验,配对t 检验等研究方法,其前提条件是数据呈现出正态性,但在实际研究中几乎不会对数据作正态性检验,默认数据是正态性分布)
SPSSAU操作截图如下:
SPSSAU输出直方图说明:
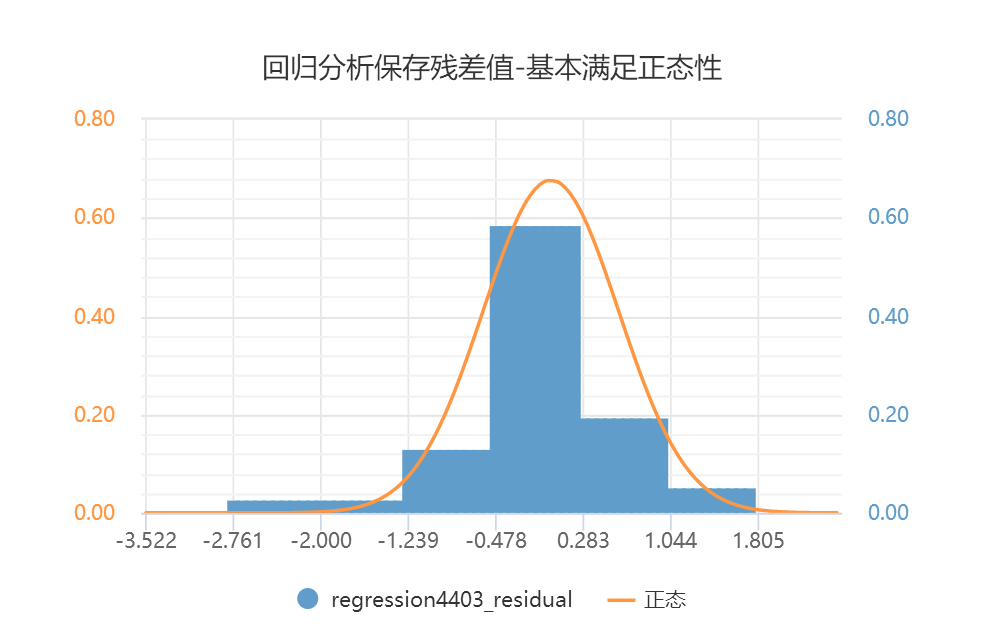
-
上图是回归分析保存的残差值进行正态性检验,上图可以看出,数据基本上满足正态性,几个柱子的分布基本上可以用一个钟形的正态曲线描绘,数据基本满足正态分布性。
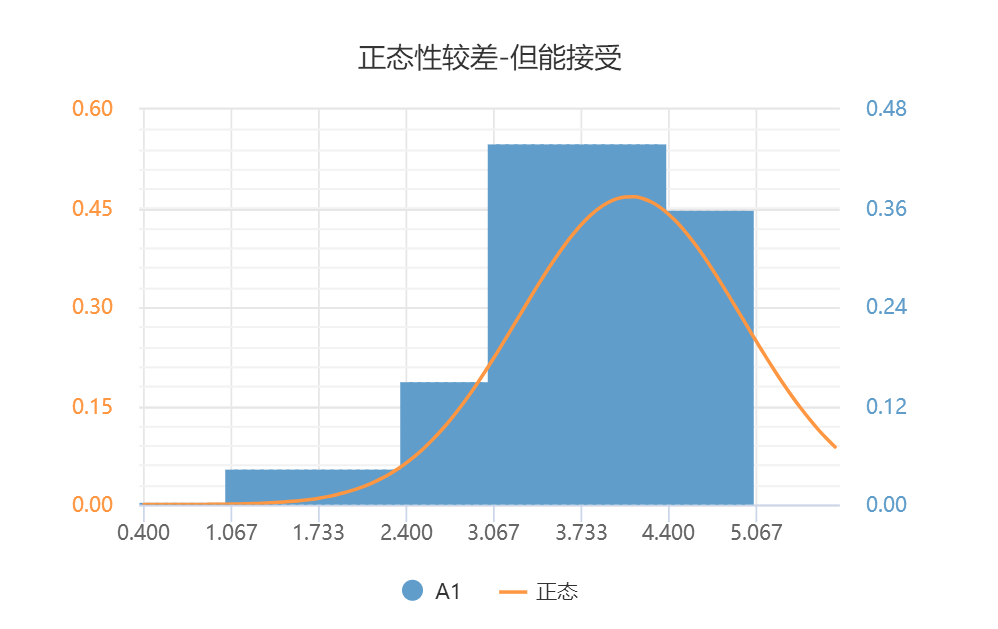
-
上图可以看出,数据离正态性较差,柱子的轮廓也有一定的钟形特征,但并不完美,如果数据量较少或要求不高,也基本上可以接受这样的正态性特质。
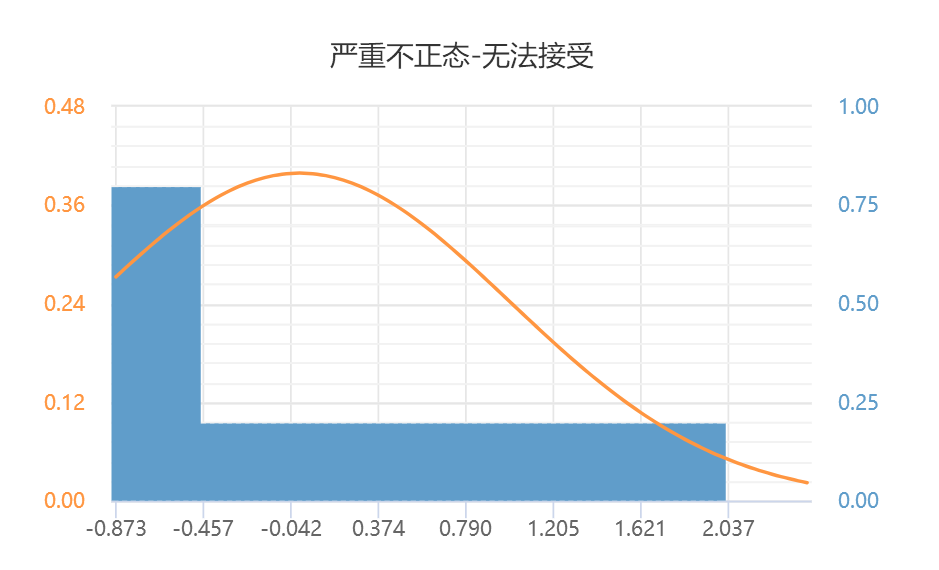
-
上图可以看出,数据明显偏差正态性,柱子轮廓完全不具有“钟形”即正态性特质,数据完全不符合正态分布。
疑难解惑
-
直方图和正态性检验结果矛盾?
-
检验数据是否正态分布有很多种方法,图示法,统计检验法,还有描述法等。统计检验法对于数据的要求最为严格,而实际数据由于样本不足等原因,即使数据总体正态但统计检验出来也显示非正态,因而一般情况下使用图示法相对较多,只要正态性情况在一定可接受范围内即可。
-
除此之外,也可以对数据取对数,开根号等(数据处理->生成变量),然后对新数据再次检验正态性。一般来说取对数,开根号等处理只会改变数据的相对值,而数据的相对意义并不会改变,因此如果使用取对数等方法让数据更‘正态’,是科学合理的做法。
