熵值是不确定性的一种度量。信息量越大,不确定性就越小,熵也就越小;信息量越小,不确定性越大,熵也越大。因而利用熵值携带的信息进行权重计算,结合各项指标的变异程度,利用信息熵这个工具,计算出各项指标的权重,为多指标综合评价提供依据。
在进行熵值法之前,如果数据方向不一致时,需要进行提前数据处理,通常为正向化或者逆向化两种处理(统称为数据归一化处理)。
-
比如:如果有3个指标分别为城市废气排放量,城市工业烟尘排放量,城市GDP;明显的,城市废气排放量,城市工业烟尘排放量这两项数字越小越好,但是城市GDP越大越好。因而城市废气排放量,城市工业烟尘排放量这两项进行逆向化处理,“城市GDP”则需要进行正向化处理。即逆向(负向)指标做逆向化处理,正向指标做正向化处理。这样处理后,数据方向就完全一致且解决掉量纲问题(正向/逆向此两种处理可同时解决方向和量纲问题)。
除了正向化,逆向化处理外,有时也会有直接取负数,倒数等方式。特别提示:如果数据处理后有负数或者0,在进行熵值法分析时会出现错误,原因在于熵值中的算法中有一项为求对数,负数或者0无法取对数。研究者需要特别注意此点。
在对数据进行处理之后,将处理后的数据进行熵值法分析。通常熵值法的使用场景情况如下:
-
配合因子分析(或主成分析)得到一级指标权重,进一步使用熵值法计算具体二级指标的权重,最终构建权重体系;
-
单独使用熵值法进行权重计算。
SPSSAU操作截图如下:
SPSSAU返回结果如下表:
| 熵值法计算权重结果汇总 | |||
| 项 | 信息熵值e | 信息效用值d | 权重系数w |
| C1 | 0.9946 | 0.0054 | 42.92% |
| C2 | 0.9960 | 0.0040 | 32.12% |
| C3 | 0.9969 | 0.0031 | 24.96% |
-
SPSSAU共输出信息熵值e,以及信息效用值d,和权重系数w。信息熵值e和信息效用值d均为中间过程值,研究者可直接忽略。
疑难解惑
-
出现null值?
-
熵值法算法中有一个内部处理为求对数,负数或者0无法取对数。如果原始数据中有负数或者0则会出现null值,建议使用筛选样本功能,或者异常值功能将数据处理好后再分析即可。
-
是否需要对数据量纲化处理,以及如何处理?
-
如果数据的量纲不同(单位不同),一般需要进行无量纲化处理。无量纲化处理常见处理办法有标准化、归一化等;
-
建议使用归一化(SPSSAU的生成变量功能),而不使用标准化(原因是标准化会导致非常多的数据出现负数,导致有效样本明显减少)。
-
如果是使用归一化处理【公式为:(X-Min)/(Max-Min)】,处理后会出现数字0,这会导出结果出现null值;建议分析前先进行筛选,或者直接将数字0设置成null值(SPSSAU的异常值功能)后再进行分析。
-
对数据正向或逆向化处理,以及如何处理?
-
如果需要对数据正向或者逆向化处理,请使用SPSSAU生成变量功能。正向化或者逆向化处理均会导致新数据中有数字0,这会导出最终结果出现null值,建议分析前先进行筛选,或者直接将数字0设置成null值(SPSSAU的异常值功能)后再进行分析。
-
分析出现null值,如何将小于等于0的数据处理成null值?
-
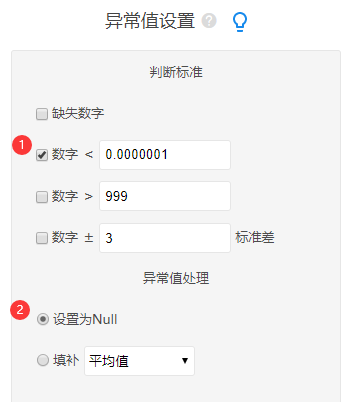
如果分析结果出现null值,原因是原始数据中有小于或者等于0的原始数据;因此将小于或等于0的数据处理即可。具体操作为:SPSSAU数据处理->异常值功能操作截图如下:
-
分析之前是否需要进行归一化、正向化或逆向化处理等?
-
如果量纲不同,一般是需要进行归一化处理等。但结合熵值法来讲,如果进行无量纲化处理(比如归一化或标准化),这会导致数据中出现数字0,这种情况会导致计算不出结果(结果显示为null值);类似的正向化、逆向化也会出现类似的情况(结果显示为null值)。
-
建议量纲不同时进行归一化处理即可(不使用标准化),但在分析前需要把数字为0的样本过滤掉(筛选样本功能),类似地,如果数据进行过正向化或逆向化处理时,也有可能出现此类情况,也一样先筛选样本再进行分析即可。
-
非负平移是什么意思?
-
熵值法的计算公式上会有取对数,因此如果小于等于0的数字取对数,则会出现null值。此种情况共有两种办法。
-
第一种:SPSSAU非负平移功能是指,如果某列(某指标)数据出现小于等于0,则让该列数据同时加上一个‘平移值’【该值为某列数据最小值的绝对值+0.01】,以便让数据全部都大于0,因而满足算法要求。
-
第二种:研究者也可以手工查看数据并将小于等于0的数据设置为异常值,但此种做法会让样本减少。
-
综合得分是什么意思?
-
熵值法得到权重值后,此时数据与对应的权重相乘,并且进行累加,最终得到一列数据即为‘综合得分’。
-
面板数据如何进行熵值法?
-
熵值法的原理是针对数据不确定性进行度量,从而计算权重。无论是什么数据(包括面板数据),均可正常的进行熵值法,一般不需要进行处理。
-
当然面板数据进行熵值法分析时,也可以先筛选出不同的年份,重复进行多次熵值法均可。
-
一般情况下面板数据只进行一次熵值法分析即可,数据格式上比如有10年且每年有100个省份,那么就为10*100=1000行数据即可(把数据重叠起来后一次性上传进行分析)。
-
只有三级指标数据无二级指标数据,如何计算二级指标权重?
-
如果只有三级指标数据但无上一级(二级指标)数据,此时如何计算二级指标权重呢。通常有以下三种办法。
-
第一:多次使用主成分分析,并且保存得到‘成分得分’,使用主成分得分来表示对应的二级指标数据;
-
第二:将所有的三级指标数据进行因子分析(进阶方法里面),然后利用方差解释率去评估二级指标的权重;
-
第三:使用主观评价方法,重新收集专家打分数据进行AHP层次分析得到权重。 类似,如果只有二级指标数据但无一级指标数据,也是类似的道理。
-
正向化或逆向化后还需要标准化吗?
-
正向化和逆向化有两个功能,首先可以将指标方向进行统一,其次是数据量纲化。因此如果进行过正向或逆向处理,数据就不需要再进一步标准化。当然再次进一步标准化也没有问题。
-
为什么分析样本量小于实际样本量?
-
如果分析时出现‘分析样本量’小于样本量,有3种可能。1是免费版(免费版仅分析前100行数据);2是做过‘筛选样本’功能(即主动设置只分析其中一部分数据);3是原始数据中有缺失数据(系统右上角‘我的数据’处可查看原始数据,也可下载原始数据等)。
-
面板数据做SPSSAU熵值法的数据格式?
-
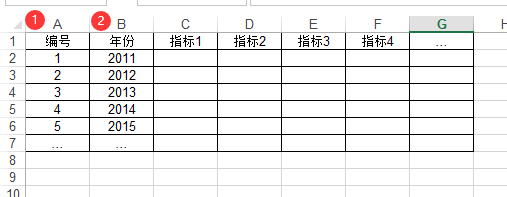
如果是面板数据希望进行熵值法,其数据格式如下图所示,比如有100家公司分别5年的指标数据,那么一共就有100*5=500行数据。数据格式上需要如此,但在分析时只需要放入‘指标列’数据即可。
-
SPSSAU熵值法计算综合得分规则说明?
-
熵值法计算综合得分,如果说做了‘非负平移’处理,而且确实原始数据满足‘非负平移’的规则,那么算法进行计算时,是以‘非负平移处理后’的数据与权重相乘累加得到综合得分。
-
如何使用组合赋权法?
-
涉及到组合赋权法的使用,可参考此页面。
-
具有层次结构的权重体系构造?
-
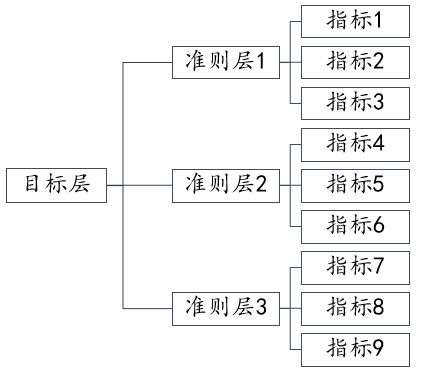
比如有三层结构如下图,通常有着指标层即指标1到指标9的数据,因此可以分别得到具体指标的权重(可考虑比如准则层1对应的3个指标做1次熵值法,准则层2的3个指标做1次熵值法,准则支3的3个指标做1次熵值)。接着3个准则层的权重如何计算呢?常见有以下几种处理办法,1是将9个指标做主成分分析并且设置为3个主成分,利用主成分方差解释率来得到3个准则层的权重;2是收集专家打分数据进行AHP层次分析法得到3个准则层的权重;3是分别做3次熵值法并且保存综合得分,分别得到准则层对应的数据(综合得分),然后利用综合得分进一步分析比如再一次熵值法或其它分析方法等。更多关于组合赋权,可参考此页面。
-