如果在进行线性回归分析时,数据中有异常值,那么常用的OLS回归估计方法得到的结论可能会产生偏差,因为OLS估计法会考虑极小化残差平方和作为标准,因为就会将异常数据纳入考虑范围中,比如下图中,OLS估计法拟合出的直线,明显不如Robust回归法(也称M估计)拟合的效果好。
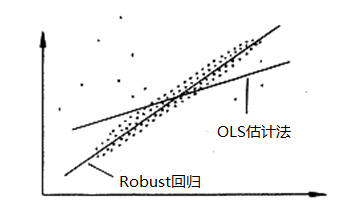
OLS回归拟合估计将异常数据同等对待,而Robust回归时会对不同的点给予不同的权重,如果某个点的残差值较小则给予更高的权重,异常点的残差值会比较大,因为其对应的权重会很小。通过不同点的残差给予不同权重,最终拟合出的结果也更加稳健可靠。关于构造权重的方法,许多学者都提出自己的方法,SPSSAU默认使用较为常见的Huber法(默认t 值取1.345)进行Robust回归。
如果数据中没有异常值,建议依旧使用传统的OLS估计法即可。即比例使用SPSSAU通用方法里面的线性回归。
Robust回归案例
-
1、背景
当前有200个研究数据,2个解释变量,1个被解释变量。现希望进行回归分析,研究2个X对于Y的影响情况。
-
2、理论
Robust回归法(也称M估计)其适用于解决异常数据(或极端数据)时的回归估计,如果说数据中没有异常值(也或者异常数据可以自行进行处理掉),那么依旧建议使用常用的ols估计法即可。
-
特别提示
-
异常数据的检查,建议使用散点图、箱线图、描述分析等进行查看,如果有极端异常数据,但是不愿意对其进行处理,此时使用robust就会比较适合。
-
Robust回归可用于结论的稳健性验证,先用ols回归法得到结论,再换用robust回归法分析,如果结论基本一致则说明结论稳健可靠。
针对本案例来看,首先进行散点图用于查看x和y的散点关系,检查是否有异常数据,如下:
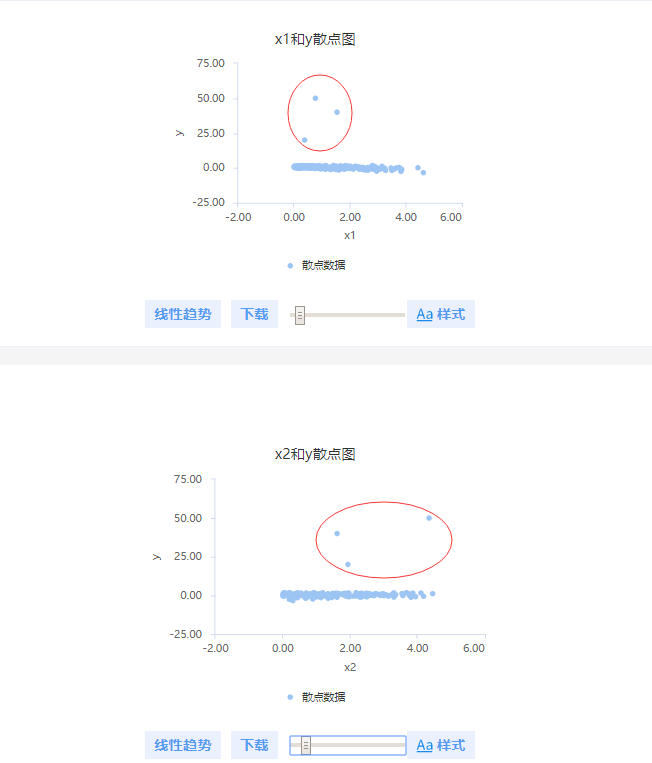
明显的可以看到,图中出现3个异常值点,如果将此3个点筛选出去,再进行分析,散点图如下:
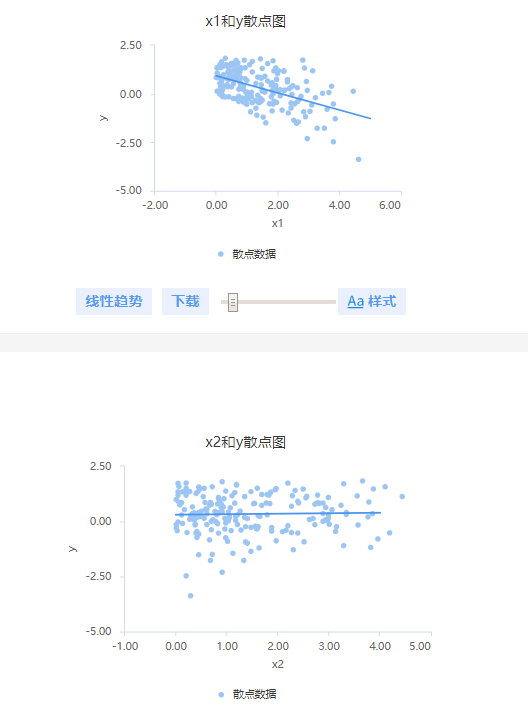
从上图可以看到,把3个异常值筛选出去后,明显可以看到,x1与y有着明显的负向关系,x2与y并没有太多联系。针对此类情况下,使用robust回归较为适合。否则可能得到完全错误的结果。
-
-
3、操作
本例子研究2个解释变量x对于1个被解释变量的影响关系,由于数据中有异常值,并且希望保留此异常数据,因此使用robust回归进行分析。操作如下:
-
4、SPSSAU输出结果
SPSSAU共输出2个表格结果,一个是常规格式,一个是简化格式。
-
5、文字分析

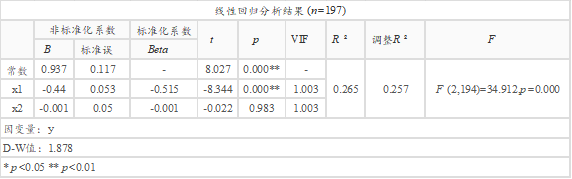
从上表格可以看到,x1呈现出0.01水平的显著性(t =-7.695,p =0.000),回归系数值为-0.423小于0,意味着x1会对于y产生显著的负向影响关系。x2的回归系数值并没有呈现出显著性,p 值大于0.05,说明x2并不会对于y产生影响关系。此结论与散点图的结论保持一致性。
-
特别提示
-
由于robust回归对残差赋予权重,因此上表格中的F 检验,R 方值和调整R 方值已经丢失原有的意义,因此不能将此3个指标值作为分析指标;
如果我们依旧使用ols回归估计方法,结果如下表可知,结论显示x1的回归系数值为-0.575(t =-1.783,p =0.076>0.05),意味着x1并不会对y产生影响关系。x2的回归系数值为0.637(t =2.133,p =0.034 <0.05),意味着x2会对y产生显著的正向影响关系。这一结论与散点图发现的情况完全相反,不可信。
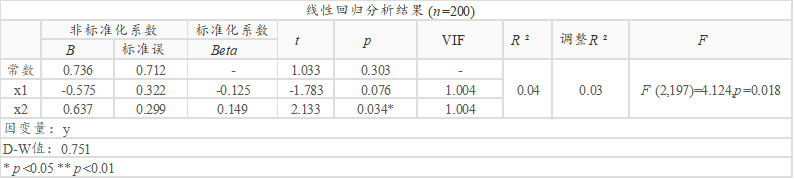
如果说将3个异常值筛选出去再进行分析,则显示x1对于y产生负向影响,x2不会影响y,这一结论与robust回归分析的结论保持一致,也正好说明robust说明可以很好的处理异常值问题,但ols回归却对异常值敏感导致不正确的结论。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
Robust回归用于解决异常值问题(也或者比如残差严重不正态等),SPSSAU默认使用Huber稳健法。
-
Robust回归可用于结论的稳健性验证,比如先用ols回归法得到结论,再换用robust回归法分析,如果结论基本一致则说明结论稳健可靠。
-
