-
如果想研究X对于Y的影响关系(Y为定量),当前通常是使用线性OLS回归,并且通过回归系数的显著性进行判断是否有影响,影响方向如何,但是OLS回归无法看出影响的趋势情况如何,而且OLS回归要求因变量Y为正态分布,并且OLS回归对于异常值较为敏感,以及OLS回归对于异方差问题也较为敏感;正态分布、异常值问题和异方差问题,当前均有着非常多的解决办法,但是回归系数的变化趋势无法查看。
如果想看出X对于Y的影响关系及影响趋势情况,则可以使用分位数回归;分位数回归可以查看X对Y的影响趋势及变化情况,而且分位数回归对于异常值、因变量正态性或者异方差问题均有着很强的稳健性。因而有时候也可以使用分位数研究回归模型的稳健性问题,即分别使用OLS回归和分位数回归的结果进行汇总,通过分析回归系数的显著性变化情况,判定模型的稳健性(稳定性)。
分位数回归(Quantile regression, QR回归),其原理是将数据按因变量进行拆分成多个分位数点,研究不同分位点情况下时的回归影响关系情况。总结来看,分位数回归主要有两个作用如下:
-
分析X对于Y的影响趋势情况;
-
用于回归模型的稳健性分析。
-
分位数回归案例
-
1、背景
当前进行一项雇员工资影响因素研究(200个样本),影响因素X共有三项,分别是‘‘起始工资’,‘受雇月数’和‘受教育年限’。因变量Y为当前工资。如下表:
变量 名称 因变量Y 当前工资 自变量X1 起始工资 自变量X2 受雇月数 自变量X3 受教育年限 当前研究显示起始工资,受雇佣月数,受雇月数和受教育年限均会对当前工资产生正向影响关系。但是现在希望研究这种影响关系是否一直稳定,有没有变化趋势,比如当前工资水平不同的群体,他们受到3个因素的影响关系是否一致,影响幅度是否有变化等。由于数据较大,因而对数据进行取对数处理后再进行分析。
-
2、理论
分位数回归是研究X对于Y的影响时,因变量Y在不同分位点时,X对于Y的影响情况。分位数回归与线性OLS回归的功能类似,但是分位数回归对于因变量的正态性没有要求,并且分位数回归对于异常值具有稳健性,以及不需要考虑异方差问题等。另外分位数回归不同于普通OLS回归,分位数回归不会有F 检验和调整R 2值等;分位数回归仅输出回归系数的检验,以及R 2值;分位数回归主要有两个作用如下:
-
分析X对于Y的影响趋势情况;
-
用于回归模型的稳健性分析。
-
-
3、操作
本例子研究3个X(‘起始工资’,‘受雇月数’和‘受教育年限’)对于因变量(Y)即当前工资的影响情况,并且将分位数点拆分成10段,分别从0.05~0.95,间隔为0.1;以便查看当前工资在不同分位点时,受到3个X的影响变化趋势情况;操作截图如下:
SPSSAU共提供三种分位数类型,第1种是分位数从0.05到0.95(间隔0.1);第2种是分位数从0.1到0.9(间隔0.1);第3种是分位数从0.25到0.75(间隔0.25);如果是想查看影响关系的趋势情况,一般使用前2种;如果仅仅是想看回归模型的稳健性情况,一般使用第3种。
-
4、SPSSAU输出结果
SPSSAU共输出表格和图形。分别如下:
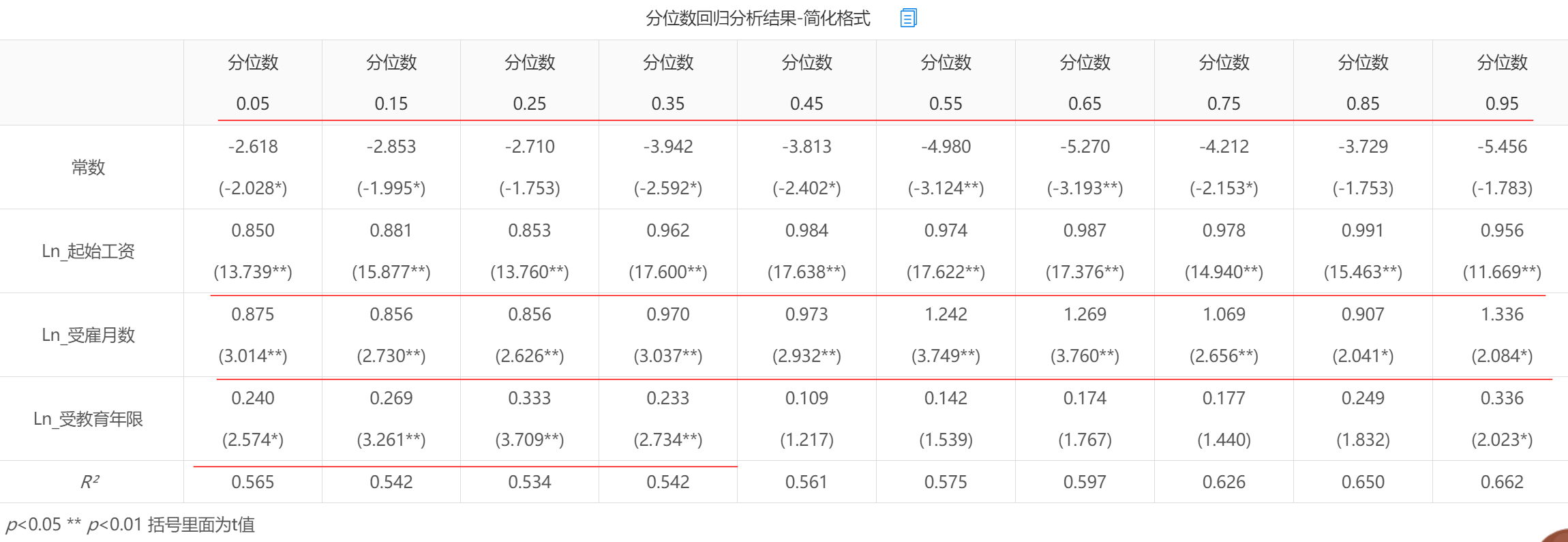
上图显示0.05~0.95(间隔0.1)共10个分位数点时,3个X(‘起始工资’,‘受雇月数’和‘受教育年限’)对于因变量(Y)即当前工资的影响情况。上表格显示,不同分位数点时,起始工资对于当前工资均会产生显著的正向影响;以及受雇月数对于当前工资也均会产生显著的正向影响。但是受教育年限对于当前工资的影响来看,当前工资分位数在0.35及以下时,受教育年限对当前工资有着显著的正向影响关系;但是当前工资分位数点高于0.35时,受教育年限对当前工资不会有影响,也即是说:当前低工资水平的群体,他们的工资水平会受到教育年限的正向影响,但是当前工资水平较高的群体,他们的工资水平就不再受到教育年限的影响。具体3个变量对于当前工资的影响趋势情况,可具体通过下面的图形进行分析。
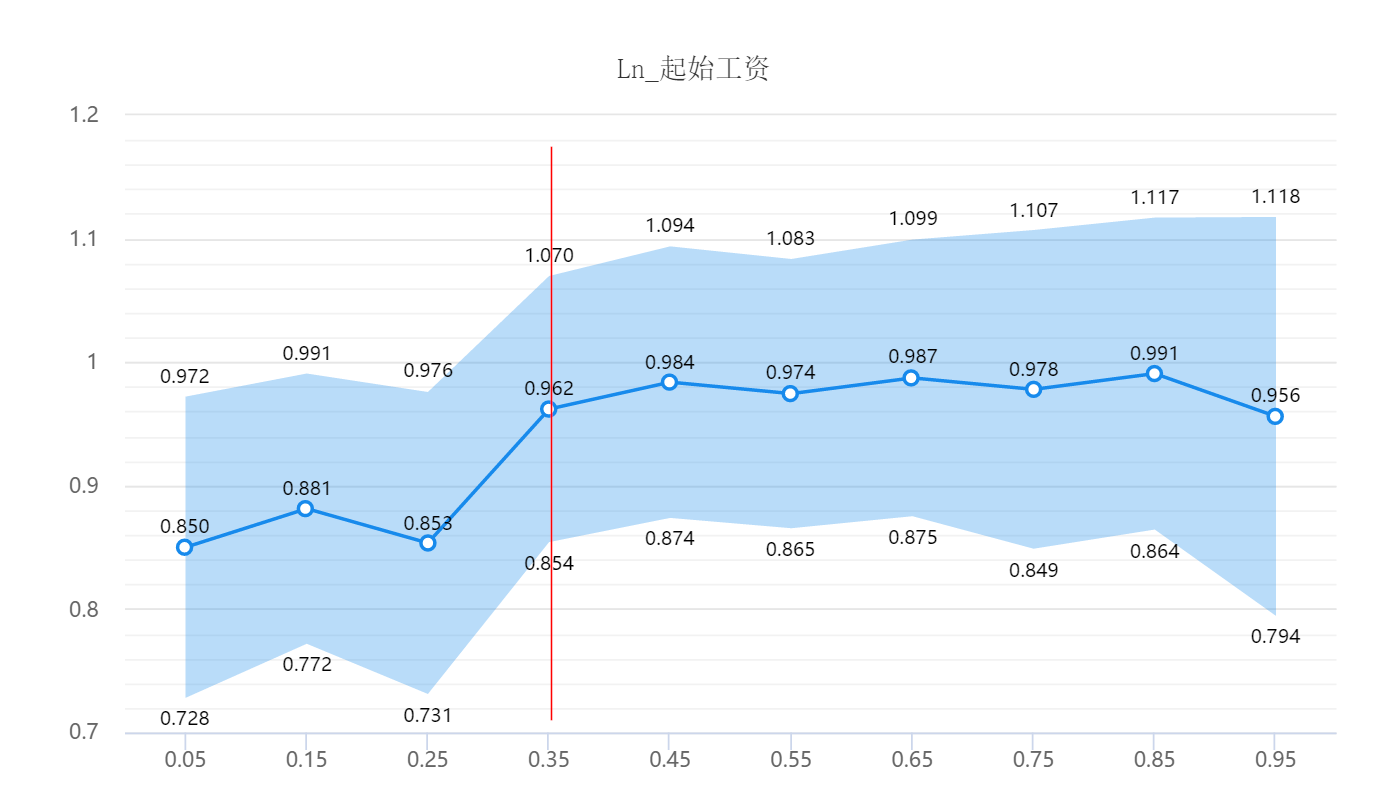
针对起始工资对于当前工资的影响来看,上图显示,在当前工资分位数水平为0.35或更低时,起始工资对于当前工资有着显著的正向影响,但是影响幅度相对较低。当前工资分位数水平高于0.35时,起始工资对当前工资有正向影响,而且影响幅度相对较低。也即说明工资水平较低的群体,他们受到起始工资的影响幅度有限;而工资水平较高的群体,他们受到起始工资的影响幅度相对较高。
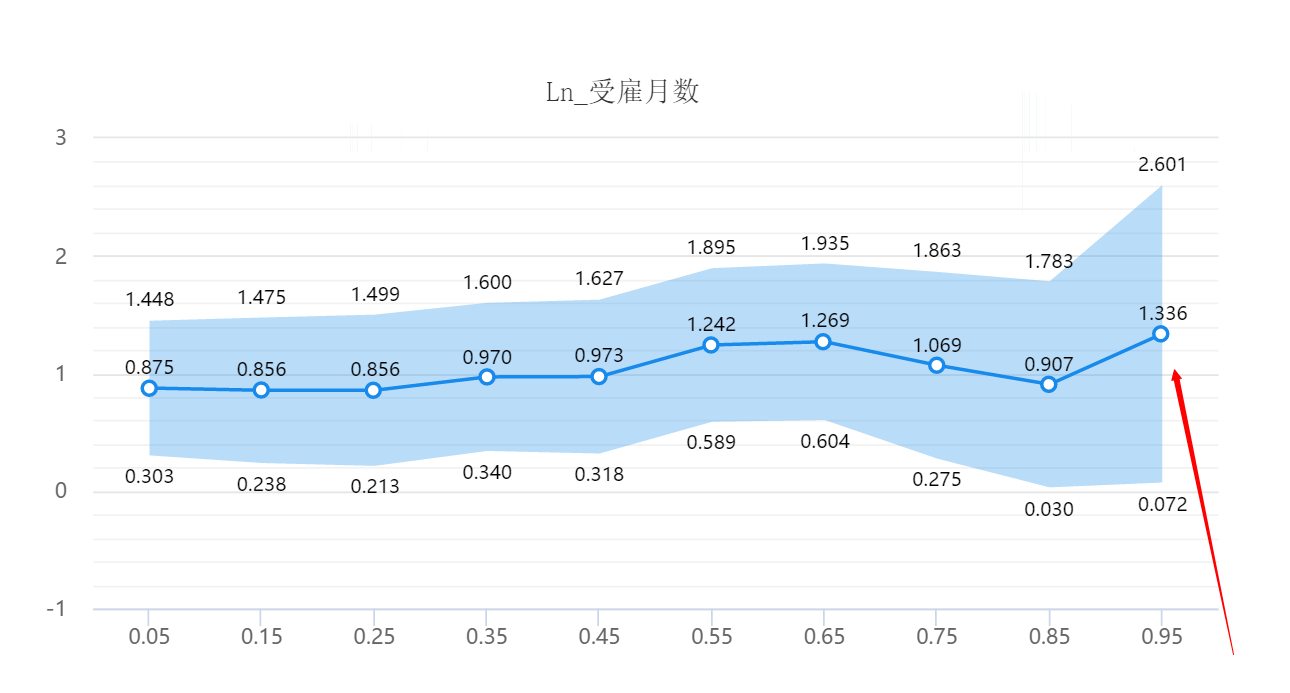
针对受雇佣月数对于当前工资的影响来看,受雇佣月数对于当前工资都有正向影响,受雇佣月数越长,当前工资水平也会越高。但是明显的看到,当前工资在0.95分位数点时,即工资水平最高的top5群体,他们工资水平受到受雇佣月数的影响明显非常高。
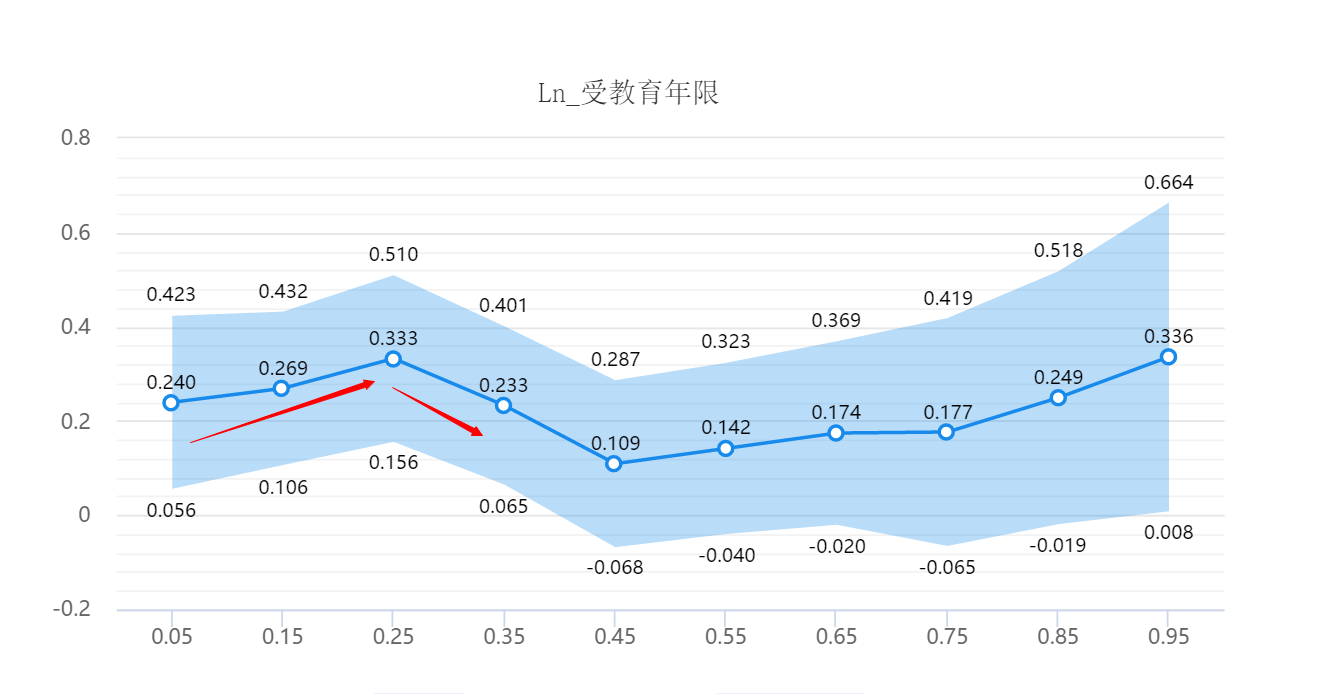
针对受教育年限对于当前工资水平的影响上,上述分析发现当前工资水平较低(低于35%分位数)的群体,他们的工资水平会受到教育年限的正向影响;但是工资水平较高(高于35%分位数)的群体,他们工资水平不会受到教育年限的影响。
从上图可知,对于当前工资水平较低(低于35%分位数)的群体,教育年限对于工资水平的影响趋势可描述为;工资水平较低群体,他们受教育年限对于工资的影响,随着工资水平提升而提升,但提升到一定程度(工资水平为25%分位点)时,教育年限对于工资的影响开始下降,并且截止到工资水平为35%分位数点后,这种影响关系会消失,工资水平不再受到受教育年限的影响。简述即为:工资较低群体,受教育年限越高,工资会越多,而且在一定范围内,这种影响关系会越来越高;但工资水平达到一定程度后,受教育年限对工资不再有任何影响关系。
-
5、文字分析
文字分析如上一部分所示,需要特别提示在于:
-
如果分析影响趋势变化情况,需要先确认是否回归系数呈现出显著性;
-
很多时候OLS回归显著有影响,但某个分位数点时却不显著;这种情况非常正常,原因在于分位数回归分析更加深入,具体到每个分位数点时的影响关系研究,而OLS回归只是一个综合概括分析。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
分位数回归通常有2个应用,第一是分析X对于Y的影响趋势情况;第二是用于回归模型的稳健性分析;
-
分位数回归对于因变量的正态性没有要求,并且分位数回归对于异常值具有稳健性,以及不需要考虑异方差问题等;
-
如果分析影响趋势变化情况,需要先确认是否回归系数呈现出显著性;
-
很多时候OLS回归显著有影响,但某个分位数点时却不显著;这种情况非常正常,原因在于分位数回归分析更加深入,具体到每个分位数点时的影响关系研究,而OLS回归只是一个综合概括分析。
-
