因子分析
-
因子分析(探索性因子分析)用于探索分析项(定量数据)应该分成几个因子(变量),比如20个量表题项应该分成几个方面较为合适;用户可自行设置因子个数,如果不设置,系统会以特征根值大于1作为判定标准设定因子个数。
因子分析通常有三个步骤;第一步是判断是否适合进行因子分析;第二步是因子与题项对应关系判断;第三步是因子命名。
-
第一步:判断是否进行因子分析,判断标准为KMO值大于0.6;
-
第二步:因子与题项对应关系判断。
-
因子与题项对应关系判断:假设预期为3个因子(变量),分析题项为10个;因子与题项交叉共得到30个数字,此数字称作”因子载荷系数”(因子载荷系数值表示分析项与因子之间的相关程度); 针对每个因子(变量),对应10个”因子载荷系数”,针对每个分析项,则有3个”因子载荷系数值”(比如0.765,-0.066,0.093),选出3个数字绝对值大于0.4的那个值(0.765),如果其对应因子1,则说明此题项应该划分在因子1下面.
-
对不合理题项进行删除:共有三种情况; 第一类:如果分析项的共同度(公因子方差)值小于0.4,则对应分析项应该作删除处理;第二类:某分析项对应的”因子载荷系数”的绝对值,全部均小于0.4,也需要删除此分析项;第三类:如果某分析项与因子对应关系出现严重偏差(通常也称作‘张冠李戴’),也需要对该分析项进行删除处理。
-
第三步:因子命名。
-
在第二步删除掉不合理题项后,并且确认因子与题项对应关系良好后,则可结合因子与题项对应关系,对因子进行命名。
-
分析项 网购满意度20个题项 因子分析说明 网购满意度由20个题表示,此20个题项可浓缩成几个大方面? -
分析结果表格示例如下(SPSSAU同时会生成碎石图):
因子载荷系数 共同度(公因子方差) 因子1 因子2 因子3 分析项1 0.765 -0.066 0.093 0.598 分析项2 0.676 0.081 -0.017 0.464 分析项3 0.657 0.207 -0.205 0.517 分析项4 0.645 0.271 0.089 0.497 分析项5 0.501 0.457 0.085 0.467 分析项6 0.311 0.697 -0.005 0.583 分析项7 0.226 -0.669 0.130 0.516 分析项8 0.191 0.644 0.046 0.453 分析项9 0.476 -0.187 0.542 0.555 分析项10 0.001 -0.048 0.968 0.939 -
特别提示
-
因子分析进行因子浓缩时,通常会经历多个重复循环,删除不合理项,并且重复多次循环,最终得到合理结果。
-
-
SPSSAU操作截图如下:
-
特别提示
-
关于“保存因子得分”:因子分析将信息浓缩成几个因子,并且可让系统保存“因子得分”,。因子得分可用于进一步分析,比如聚类分析,回归分析使用等。
-
关于“保存综合得分”:如果使用因子分析的目的在于进行综合竞争力排名,比如银行的绩效排名,上市公司竞争力排名等,此时可直接保存综合得分,用于竞争力排名。
-
-
因子分析案例
-
1、背景
当前有一份数据,共涉及A1~A4,B1~B4,C1~C3,D1~D3共14个量表题,希望将此14个量表题使用因子分析浓缩成几个维度。从背景情况上看,预期此14个题目可分为4个维度,分别称作A,B,C和D维度。当然有可能个别项并不合适,因此有可能对其进行删除处理。
-
2、理论
因子分析是一种信息浓缩的分析方法,比如此例中有14项,此14项可以浓缩成几个关键词描述。好比一个人说了14句话,事实上可以用四个词语直接描述即可。当然14句话最终用四个词语表示,那么信息肯定有一些丢失(方差解释率表达4个词语可以提取出14项的信息量)。以及14个句话可以和4个词语进行对应起来。最核心的其实是找出对应关系,这才是关键。
-
一般情况下,如果14项与4个维度之间的对应关系情况,与专业知识情况不符合,比如A1被划分到了C维度下面,此时则说明可能A1这项应该被删除处理,其出现了‘张冠李戴’现象。因而在进行分析时很可能会对部分不合理项进行删除处理。
-
关于维度(因子)和题项对应关系,维度(因子)和题项之间交叉会得到一个‘因子载荷系数’,此系数绝对值大于0.4,则说明二者有着较强关联性,该题项可以与该维度(因子)有着对应关系。
-
单独提示
-
有时候会出现‘纠缠不清’现象,比如A1可归属为A维度,同时也可归属到C维度,这种情况较为正常(称作‘纠缠不清’),需要结合实际情况处理即可,可将A1删除,也可不删除,带有一定主观性。因子分析是一个多次重复的过程,比如删除某个或多个题项后,则需要重新再次分析进行对比选择等。最终目的在于:维度与分析项对应关系,与专业知识情况基本吻合。
-
再次提示
-
题项和因子(维度)对应关系判断规则:某项对应某因子的因子载荷系数绝对值大于0.4,则说明该项对应该因子。
-
‘张冠李戴’:其指比如A1本来应该划分在A维度,但分到其它维度比如B维度中;此种情况最终不能被接受,需要删除A1这项。
-
‘纠缠不清’:其指比如A1可归属到A维度,也可以归属到B维度,此种情况最终可被接受,A1这项可视情况归为A或B维度均可。
-
-
3、操作
-
Step1: 第一次分析
本例子中A1~A4,B1~B4,C1~C3,D1~D3共14个量表题,此14个题目共分为4个维度,因此在分析前可主动告诉SPSSAU,此14项是四个因子,否则SPSSAU会自动判断多少个因子(通常软件自动判断与实际情况有很大出入,所以建议主动设置因子个数)。如下图:
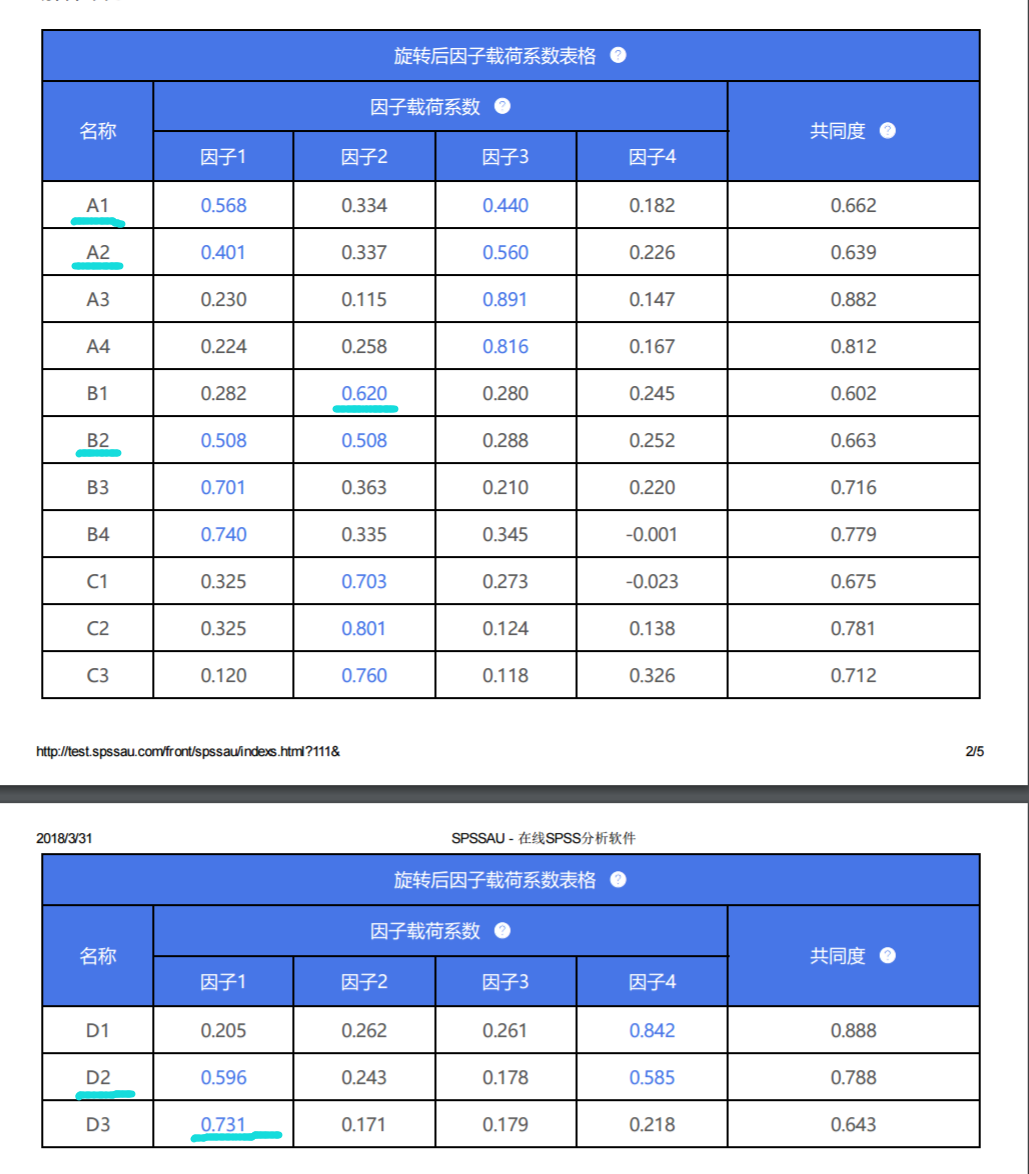
完成后结果如下:
-
A1~A4这4项,它们全部对应着因子3时,因子载荷系数值均高于0.4,说明此4项应该同属于一个维度,即逻辑上A1~A4这4项,并没有出现‘张冠李戴’现象。但是A1和A2这两项出现‘纠缠不清’现象,A1和A2除了可以对应因子3,也可以放在因子1下面。一般出现‘纠缠不清’现象时,暂时保留,先处理清楚‘张冠李戴’问题更好。
-
B1~B4共4项,B2,B3,B4这3项对应着因子1下面,但是B1却对应着因子2,因此B1这项属于‘张冠李戴’,应该将B1删除。B2同时对应因子1和因子2均可,属于‘纠缠不清’,暂不处理B2。
-
C1~C3共3项,此3项均对应着因子2,此3项并没有出现‘纠缠不清’或者‘张冠李戴’问题。
-
D1~D3共3项,D3出现了‘张冠李戴’问题,应该进行删除处理。D2出现了‘纠缠不清问题’(可对应因子1和因子4),应该给予关注。
-
总结上述分析可知:B1和D3这两项出现‘张冠李戴’,应该首先将此两项删除;而A1,A2,B2,D2共四项有出现‘纠缠不清现象’,暂时不处理(进行关注即可)。将B1和D3这两项删除后,进行第二次分析。
从上图中可以看出:
-
-
Step2: 第二次分析
将B1和D3这两项删除后,进行第二次分析。结果如下:
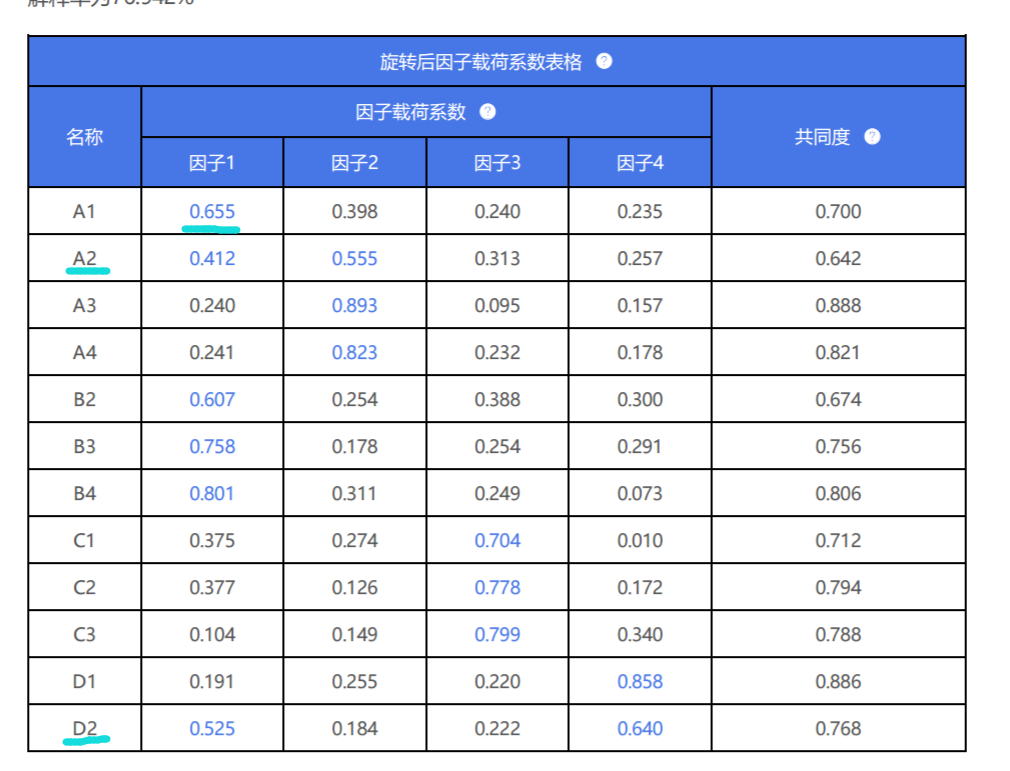
-
A1出现‘张冠李戴’现象,应该删除,A2出现‘纠缠不清’现象,暂不处理,但应该给予关注
-
B2~B4共3项没有问题
-
C1~C3共3项没有问题。
-
D2出现‘纠缠不清现象’
-
总结可知:应该将A1先删除后再次进行第3次分析,另对A2和D2这两项给予关注。
从上图可知
-
-
Step3: 第三次分析
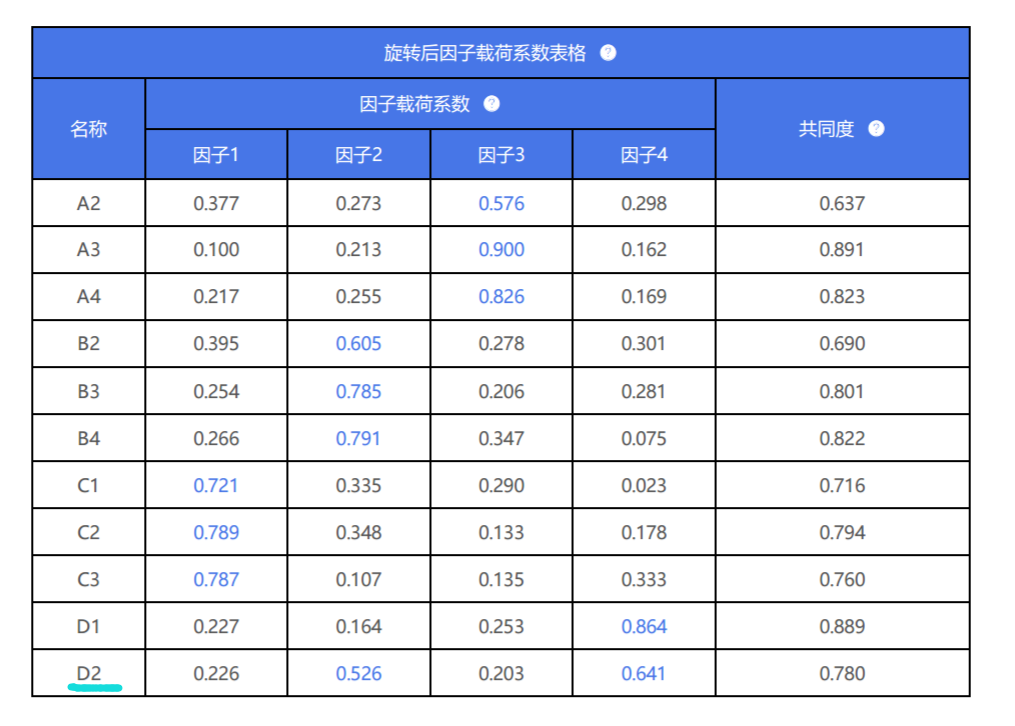
将A2先删除后再次分析结果如下:
-
从上图可知
-
D2可同时出现在因子2和因子4下面,但考虑到D维度当前仅余下2项,因而表示可以接受,最终是将D2归纳到因子4即D维度下面。最终找出A,B,C和D共4个维度,它们分别与项之间的对应关系良好。因子分析结束。
-
-
-
4、SPSSAU输出结果

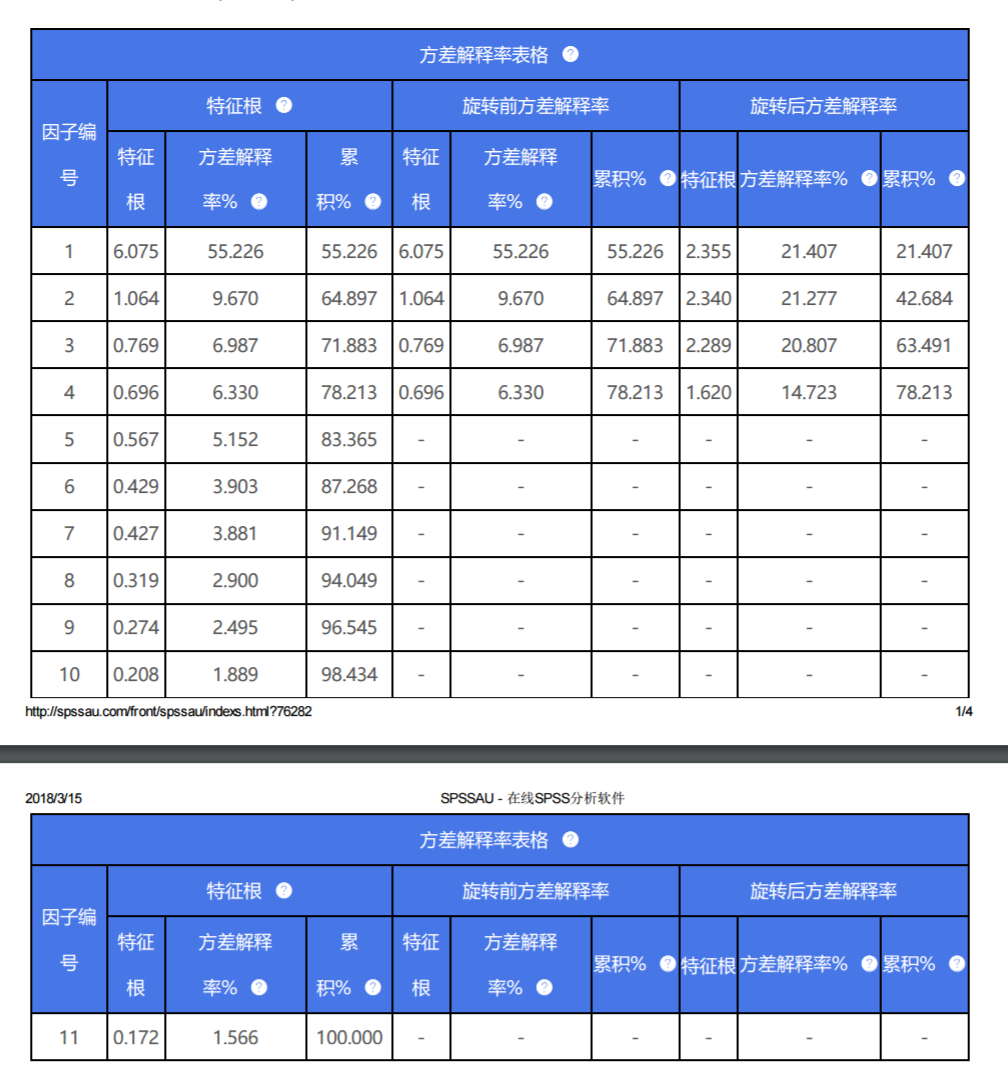
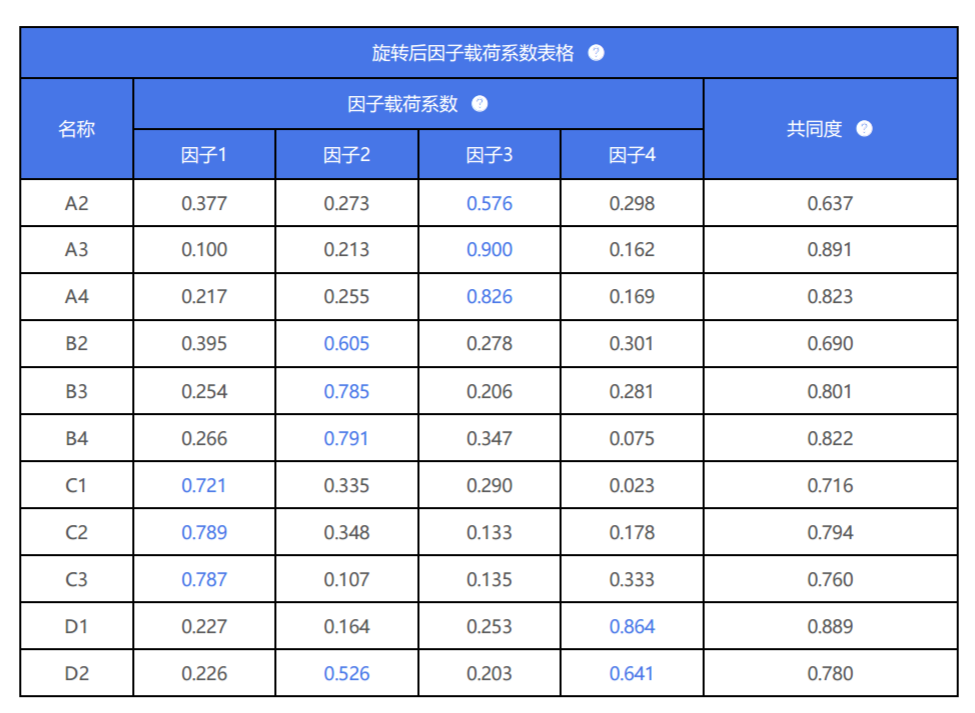
将最终处理好的结果作为最终结果,并且进行描述即可,由于中间过程可能会非常多,因而不需要具体报告中间过程表格。
-
5、文字分析
-
针对第一个表格:
从上表可知:使用因子分析对14个项进行分析,并且因子分析使用最大方差旋转法进行旋转。因子分析时,KMO值为0.876>0.6,通过巴特球形检验,说明本次数据非常适合进行因子分析。
-
针对第二个表格:
从上表可知:累积方差解释率值为78.213%,说明提取出来的4个因子可以提取出总共11项中78.213%的信息量,而且四个因子的方差解释率(信息提取量)分别为:21.407%,21.277%,20.807%和14.723%。信息提取量分布较为均匀,综合说明本次因子分析结果良好。
-
针对第三个表格:
从上表可知:使用因子分析对14个项进行浓缩处理。最终浓缩为四个因子,在进行第一次分析时发现B1和D3这两项,它们与预期对应关系情况,和专业情况不符合(另外一种写法是因子载荷系数值小于0.4,本应该对应该维度时因子载荷系数大于0.4,但是却低于0.4了),因而删除此两项后进行第二次分析,第二次分析时删除掉A1这个题项。最终余下11个题项,此11项与预期对应关系情况良好,与专业预期相符。结合因子与分析项的对应关系情况,最终对浓缩出来的四个因子进行分别命名为:A,B,C和D维度。
-
-
特别提示
-
因子分析时还会输出一个表格叫“成分得分矩阵”,如果涉及到权重计算,此会使用此表格。
-
因子分析后通常还需要将因子综合,比如此例子得到4个因子,4个因子分别与项之间有对应关系,如何将项概括起来呢。有以下两种办法:
-
因子分析后通常还需要将因子综合,比如此例子得到4个因子,4个因子分别与项之间有对应关系,如何将项概括起来呢。有以下两种办法:
-
1:计算平均值(此种做法通常是针对问卷,其它数据并不符合)
-
2:使用因子得分,如下图操作
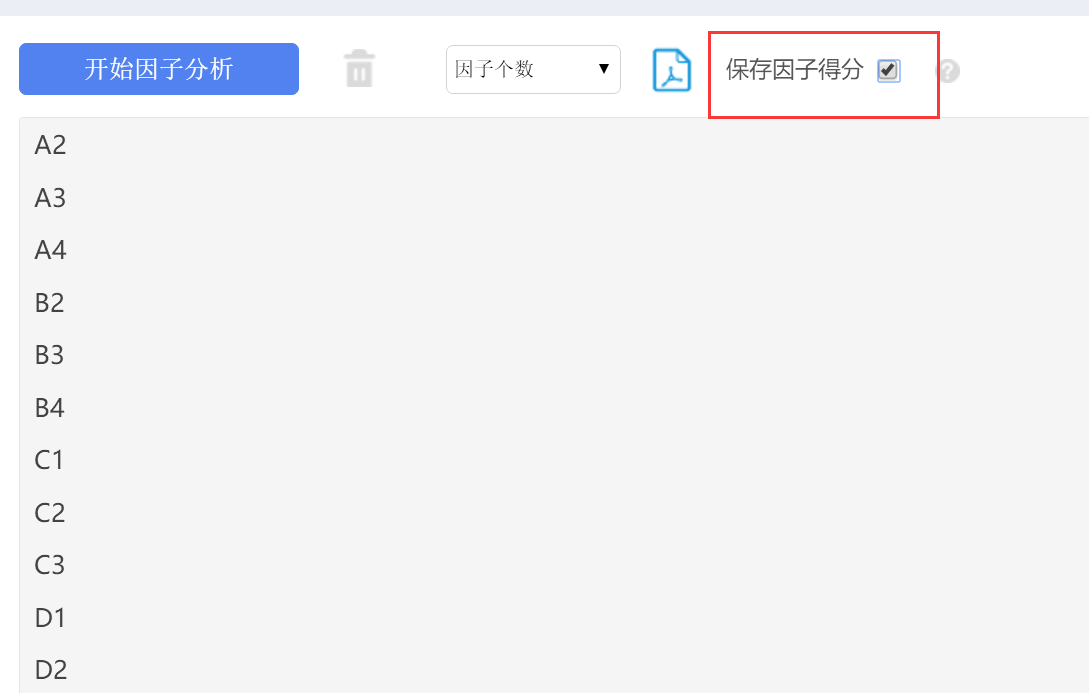
-
-
-
6、剖析
因子分析涉及以下几个关键点,分别如下:
-
区分‘张冠李戴’和‘纠缠不清’这两种现象;
-
通常先处理掉‘张冠李戴’现象,然后自然的到后面‘纠缠不清’问题会减少,后续即使有个别‘纠缠不清’现象时,也基本可以接受。
-
通常需要首先设置好因子个数,而不是让软件自动识别。
-
需要来回多次进行对比,找出最佳结果。
-
同样的样本数据,不同的分析思路,有可能出现结果不相同,但只要符合因子的思维概念即可。
-
因子分析结束后,还需要用得到的几个因子,用于后续分析使用,通常可使用因子得分(问卷常使用平均分)继续后续用于回归分析,聚类分析等。
-
疑难解惑
-
同源方差或共同方法变异偏差,Harman单因子检验?
-
同源方差是指测量方法(比如问卷收集数据)带来的可能潜在误差。如何测量呢?通常情况下是使用Harman单因子检验方法。即:把所有量表项进行因子分析时,如果只得出一个因子或者第一个因子的解释力(方差解释率)特别大【具体多大建议以文献为准,通常50%则非常大】,此时可判定存在同源方差(共同方法偏差)。
-
同源方差的检验还有其它方法,比如验证性因子分析(CFA),问卷研究》验证性因子分析,具体请查看对应方法的帮助手册。
-
提示出现奇异矩阵?
-
如果提示出现“奇异矩阵”,通常情况下有以下三个原因及解决办法。
-
第一、由于分析样本量太少(比如分析项有20个,分析样本仅10个),此里需要加大样本量或者减少分析项即可;
-
第二、分析项之间的相关性非常非常强(相关系数大于0.8,甚至接近1),共线性严重,建议使用相关分析,然后把相关系数值非常大的项移除出去后再次分析;
-
第三、分析项之间的相关性非常非常弱(相关系数接近0),建议使用相关分析,然后把相关系数值非常小的项移除出去后再次分析。
-
因子得分和综合得分?

-
因子分析将信息浓缩成少数几个因子,如果选中“因子得分”,此时可SPSSAU会保存起来,名字比如为:FAC****_score1。因子得分可用于进一步的分析,比如聚类分析使用等。
-
如果使用因子分析的目的在于进行综合竞争力排名,比如银行的绩效排名,上市公司竞争力排名等,此时可直接保存综合得分,用于竞争力排名。SPSSAU会新生成一个标题名字比如为: Comp_score****,综合得分数据通常需要手工下载然后在EXCEL里面再次使用(比如排序等),可使用右上角‘数据管理’,把原始数据下载出来。
-
因子分析计算权重?
-
如果使用因子分析的目的在于计算权重,此时可使用旋转后方差解释率值进行权重计算。比如提取2个因子,旋转后的方差解释率分别是39.759%,24.061%,旋转后累积方差解释率为63.820%。那么归一化(即除累积方差解释率)即得到权重,计算如下表:
| 名称 | 旋转后方差解释率 | 权重 |
|---|---|---|
| 因子1 | 39.759% | =39.759%/63.820%=62.30% |
| 因子2 | 24.061% | =24.061%/63.820%=37.79% |
-
KMO值过低?
-
一般需要KMO值大于0.6即可,如果是两个分析项,KMO值一定是0.5;因而建议删除掉共同度(公因子方差)值较低项,这样可以提升KMO值。
-
如果不输出KMO值,意味着数据质量过差,建议可使用相关分析看下相关关系,如果相关系数值基本均小于0.3(或者没有呈现出显著性),则说明题项间关联性弱,则KMO值一定会较低,建议先移除相关系数值较低项后再次分析。
-
提示:KMO值综合衡量分析项间的信息重叠情况(即分析项之间的相关关系情况)。分析项之间的相关系数过低(比如小于0.2或没有显著性),信息重叠度低无法有效浓缩信息,这会导致KMO值较低,如果分析项之间的相关系数过高(比如大于0.8),这会导致严重共线性可能无法输出KMO值。分析项之间的相关系数值一般希望介于0.3~0.7之间较好。
-
无论如何均‘张冠李戴’或‘纠缠不清’?
-
‘张冠李戴’是需要处理的,如果无论如何都有‘张冠李戴’现象,意味着维度和题项间对应关系有问题。可考虑减少因子个数进行对比分析。【特别提示:因子分析是一个来回多次重复对比,结合软件输出和自身专业知识情况综合选择对比找出最优结果的过程】
-
‘纠缠不清’这种现象,多数时候并不需要处理。
-
因子分析相关名词解释?
| 术语 | 说明 |
|---|---|
| KMO值 | 一个用于检验是否适合因子分析的指标,一般大于0.6即可。 |
| Bartlett球形度检验 | 对应的p 值小于0.05则说明适合进行因子分析。 |
| 特征根 | 自动识别因子最佳个数的指标,通常大于1作为标准。实际应用中,多数时候是自行设置因子个数。 |
| 方差解释率 | 因子提取的信息量,比如21.651%,意味着该因子提取出所有分析项21.651%的信息量表,方差解释率直接就可理解为权重值。 |
| 累积方差解释率 | 所有因子提取出的信息量,该指标值一般大于50%即可。 |
| 最大方差旋转法(Varimax) | 一种旋转方法,类似于‘魔方’的六种颜色需要对应在一起。一般使用最大方差旋转法。 |
| 共同度(公因子方差) | 可用于衡量分析项是否有意义的项,一般小于0.4说明该项需要被删除。 |
| 因子载荷系数 | 用于衡量因子和分析项对应关系的指标,其绝对值大于0.4,则说明分析项应隶属于对应的因子。 |
| 成分得分 | 中间计算过程值,通常意义很小。 |
| 碎石图 | 将特征根以图示形式展示,用于辅助判断因子个数。 |
-
最大方差旋转问题?
-
SPSSAU默认使用最大方差旋转法(Varimax)对数据进行旋转。特征根,方差解释率和累积方差解释率这三项均区分旋转前和旋转后;如果让软件自动识别因子个数,是以旋转前特征根大于1作为标准;其余情况下的分析建议以旋转后作为标准。
-
因子得分后用于后续分析比如聚类分析等?
-
因子得分可用于进一步分析使用如果进行聚类分析使用等,因子得分需要选中按钮才会生效,且SPSSAU单独生成新标题名称类似为:“FAC****_score1”。用户可通过【数据处理->标题处理】对名称进行修改即可。

-
综合得分如何使用?
-
综合得分可用于对比综合竞争力情况,综合得分值越高,此时综合竞争力越强。此类应用常见于经济、管理类研究,比如上市公司的竞争实力对比。
-
综合得分需要选中按钮才会生效,且SPSSAU单独生成一列新标题名称类似为:“Comp_score****”,一般情况下用户需要把综合得分的原始数据下载出来使用,通过右上角‘我的数据->下载’,可将综合得分下载出来使用。

-
因子分析提示“出错啦”或者“非正定矩阵”?
-
1、因子分析时,放错分析项(重要提示: 效度分析仅仅是针对量表数据)
-
2、数据质量过差。
-
3、样本量过少,比如仅30个样本
-
4、如果是问卷数据,请使用‘描述分析’检查,数据中是否有‘-2’,‘-3’之类的异常值(如果有,请先把数据下载,清除掉此类异常数据【直接替换为空】后再上传分析)
-
5、分析项之间的相关关系非常强(使用相关分析进行检查)
-
解决办法
-
如果是放错分析项,将非量表数据放入,则重新放置分析项即可
-
加大样本量,通常建议100以上的样本量
-
移除相关关系非常强的项后重新分析
-
因子分析时,KMO值为null不存在?
-
1、原理上因子分析要求各个分析项之间有着适中的相关关系(不能过高或过低)。如果分析项之间的相关系数值过高(比如大于0.8),说明共线性太强,无法有效浓缩信息,此种情况可能导致KMO值无法输出。建议在进行因子分析前可先进行相关分析进行查看各分析项间的相关系数情况,移除掉相关系数值过高项之后,再次进行分析即可。
-
2、样本量过少容易导致相关系数过高,一般希望分析样本量大于5倍分析项个数。
-
3、提示:KMO值综合衡量分析项间的信息重叠情况(即分析项之间的相关关系情况)。分析项之间的相关系数过低(比如小于0.2或没有显著性),信息重叠度低无法有效浓缩信息,这会导致KMO值较低,如果分析项之间的相关系数过高(比如大于0.8),这会导致严重共线性可能无法输出KMO值。分析项之间的相关系数值一般希望介于0.3~0.7之间较好。
-
解决办法
-
先检查相关关系情况,并且移除掉相关系数过高项后再次分析;
-
加大样本量,建议分析样本量大于5倍分析项个数。
-
"纠缠不清"时如何处理?
-
实际分析过程中‘纠缠不清’非常普通,通常情况下并不需要做任何处理。当然如何题比较多,也可以考虑移除掉‘纠缠不清’的项。具体如何处理没有固定标准,取决于研究人员的对比尝试,选择出最优结果即可。但张冠李戴一定是需要处理掉的。
-
‘分析之前是否需要对数据进行标准化处理’?
-
SPSSAU默认就已经进行过标准化处理,因此不需要再对数据处理。当然标准化后的数据再次标准化依旧还是自身没有任何变化,结果永远均一致。
-
综合得分如何计算得到的?
-
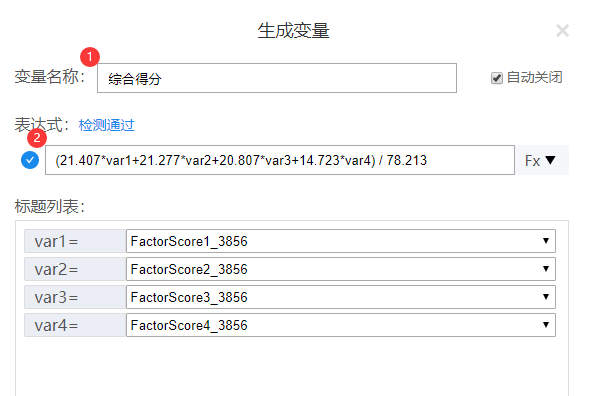
SPSSAU默认提供保存综合得分,至于其计算原理,比如说提取得到4个因子,并且此4个因子的旋转后方差解释率分别是21.407%,21.277%,20.807%和14.723%;累积方差解释率值为78.213%。综合得分计算公式为:求和(因子得分*旋转后方差解释率)/累积方差解释率。如下图所示:
-
综合得分如何使用?
-
SPSSAU默认可保存综合得分(以及因子得分等);一般该值越大表示越有竞争力等;研究者通常需要把综合得分的具体数据下载后使用,并且在EXCEL进行排序(也可使用SPSSAU生成变量里面的排序功能)。 通过右上角我的数据可下载具体综合得分的具体数据等。
-
特征根值没有大于1可以吗?
-
因子分析时通常需要综合自己的专业知识,以及软件结果进行综合判断,即使是特征根值小于1,也一样可以提取因子。
-
载荷图?
-
载荷图是针对成分(或因子)与旋转后载荷值关系的图形化展示,使用较少,通常需要手工加‘圆圈’把挨在一起的因子圈起来,更直观展示成分(或因子)与分析项的隶属对应关系情况。由于可读性和解释性问题,一般只关注于方差解释率靠前的前面几个成分(或因子),多数情况下只关注2个。
-
为什么没有出现‘成份得分系数矩阵’,因子得分,综合得分?
-
如果说因子分析计算过程中出现无法计算成成份得分(通常是内部算法出现矩阵不可逆),此时默认不输出‘成份得分系数矩阵’,同时如果选中因子得分或综合得分,此两项也无法计算,因此也不进行输出。
-
累积方差解释率出现100%以上如何办?
-
正常情况下,累积方差解释率会小于100%,但如果数据的共线性问题太严重,有可能出现方差解释率值大于100%,此时建议进行相关分析,找出相关性太强(比如相关系数大于0.8)的项,然后从分析框中移出后再次分析。与此同时,如果样本量太少也可能出现此问题建议加大样本量即可。
-
深入理解因子分析对应关系的调整?
-
关于如何调整因子与分析项对应关系,更多可查看此页面详细说明。
-
交叉载荷是什么意思?
-
比如分析项A本希望对应着因子1,那么分析项A与因子2或因子3等的载荷系数就称为‘交叉载荷系数’。通常是希望‘交叉载荷系数’小于0.4,越小越好。
-
出现共同方法偏差如何办?
-
如果出现共同方法偏差问题,建议删除不合理分析项再次分析。
-
指标计算权重?
-
因子的原理在于信息浓缩,对于信息浓缩的帮助越大,指标权重可越大,正是利用此原理,可进行指标权重的计算。信息浓缩的帮助情况使用载荷系数值进行表示。在计算指标权重时,共分为3步:
-
第1步:计算线性组合系数,其公式为:loading矩阵/Sqrt(eigen),即载荷系数除以对应特征根的平方根。可以看出,线性组合系数可用于表述了信息浓缩的大小;
-
第2步:计算综合得分系数,公式为:累积(线性组合系数*方差解释率)/累积方差解释率,即线性组合系数分别与方差解释率相乘后累加,然后除以累积方差解释率,此处为旋转后的方差解释率或累积方差解释率;
-
第3步:计算权重,将综合得分系数进行归一化处理即得到各指标权重值;
-
特别说明:从数学角度上有可能得到的权重值为负数,如果出现负数,SPSSAU会自动对loading绝对值然后再进行权重计算。
-
SPSSAU时,面板数据如何进行因子分析?
-
面板数据可直接进行因子分析,面板数据格式相对较为特殊,在分析上直接针对研究指标进行分析即可,数据格式可点击查看。
-
SPSSAU时,因子得分是标准化后的数据进行吗?
-
因子得分的数据计算,默认是基于标准化后的数据进行。
-
SPSSAU输出MSA指标?
-
进行因子分析或主成分析时,选择‘相关系数矩阵’时,SPSSAU则会输出MSA指标和相关系数矩阵信息等,其用于分析研究项是否适合进行因子分析,如果MSA指标值过低时,可考虑将该类项从模型中移出去。
-
因子分析时旋转方法如何选择?
-
因子分析时默认是使用最大方差旋转法Varimax,其会让各因子一直都保持正交状态,Varimax法使用最多。当然也可使用Promax法,其是在Varimax法基础上进行斜交旋转,使用Promax法后,各因子之间则不在完全正交,各因子之间会存在着相关关系,其使用相对较少。多数情况下使用Varimax法,但也可以尝试对比使用Promax法,二者的使用并无固定标准,通常以结果情况和文献参考为准。
-
保存因子得分或综合得分,但并没有保存?
-
在主成分分析或者因子分析时,如果选中保存因子得分(或者综合得分),但分析后标题框中未出现新的标题来标识,原因在于在计算因子得分(或综合得分)时,出现矩阵不可逆无法计算,因而无法保存。研究者应该使用共线性分析,检查数据是否存在严重的共线性问题(特征是相关系数基本接近于1或者-1),以及累积方差解释率会出现两个(甚至多个)为100%甚至高于100%的情况。将共线性严重的项移除出去不分析再做分析即可正常得到。
