灰色预测模型可针对数量非常少(比如仅4个),数据完整性和可靠性较低的数据序列进行有效预测,其利用微分方程来充分挖掘数据的本质,建模所需信息少,精度较高,运算简便,易于检验,也不用考虑分布规律或变化趋势等。但灰色预测模型一般只适用于短期预测,只适合指数增长的预测,比如人口数量,航班数量,用水量预测,工业产值预测等。
灰色预测模型有很多,GM(1,1)模型使用最为广泛,第1个数字表示进行一阶微分,第2个数字1表示只包含1个数据序列。
-
特别提示:
-
GM(1,1)模型仅适用于中短期预测,不建议进行长期预测;
-
GM(1,1)模型适用于数量少(比如20个以内)时使用,大量数据时不适合。
灰色预测模型案例
-
1、背景
当前某城市1986~1992共7年的道路交通噪声平均声级数据,现希望预测出往后一期器械声平均声级数据。数据如下:
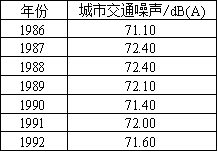
2、理论
灰色预测GM(1,1)模型一般针对数据量少,有一定指数增长趋势的数据。在进行模型构建时,通常包括以下步骤:
-
第一步:级比值检验;
-
此步骤目的在于数据序列是否有着适合的规律性,是否可得到满意的模型等,该步骤仅为初步检验,意义相对较小。级比值=上一期值 / 当期值。一般情况下级比值介于(e^(-2/(n+1)), e^(2/n+1))之间(其中e为自然对数值,n为分析的样本量)间则说明很可能会得到满意的模型,但并不绝对。
-
第二步:后验差比检验;
-
在进行模型构建后,会得到后验差比C值,该值为残差方差 / 数据方差;其用于衡量模型的拟合精度情况,C值越小越好,一般小于0.65即可。
-
第三步:模型拟合和预测;
-
进行模型构建后得到模型拟合值,以及最近12期的预测值(SPSSAU默认提供最近12期预测值)
-
第四步:模型残差检验。
-
模型残差检验为事后多重比较法。主要查看相对误差值和级比偏差值。相对误差值=残差值绝对值 / 原始值。相对误差值越小越好,一般情况下小于20%即说明拟合良好。级比偏差值也用于衡量拟合情况和实际情况的偏差,一般该值小于0.2即可。
-
特别提示:
-
GM(1,1)模型仅适用于中短期预测,不建议进行长期预测;
-
GM(1,1)模型适用于数量少(比如20个以内)时使用,大量数据时不适合;
-
GM(1,1)模型有提供级比值检验,后验差比检验,模型残差检验等;并非所有检验均能完美,通常在可容忍范围内即可。
3、操作
本例子针对某城市1986~1992共7年的道路交通噪声平均声级数据进行预测,操作如下:
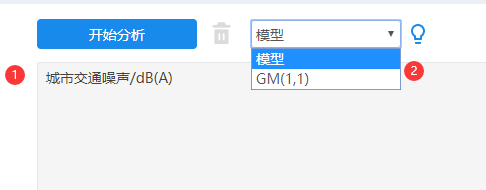
4、SPSSAU输出结果
SPSSAU共输出4个表格和1个模型拟合预测图。分别为:
-
GM(1,1)模型级比值表格
-
模型构建结果
-
模型预测值表格
-
GM(1,1)模型检验表
-
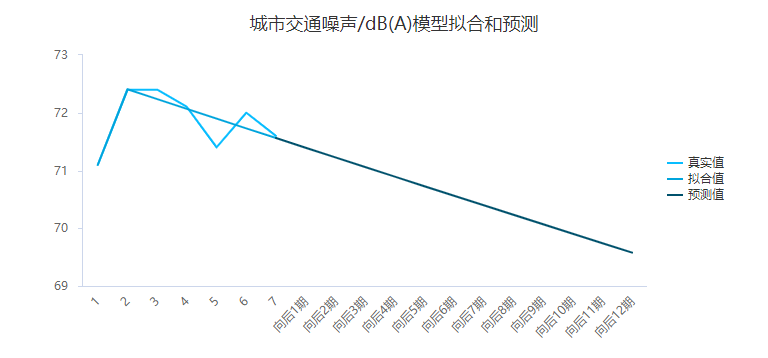
模型拟合和预测(图)
5、文字分析

从上表可知,针对城市交通噪声/dB(A)进行GM(1,1)模型构建,首先进行级比值检验,用于判断数据序列进行模型构建的适用性。级比值为上一期数据/当期数据。结果显示:级比值的最大值为1.010,级比检验值均在标准范围区间[0.779, 1.284]内(0.779和1.284由公式计算得到),意味着本数据适合进行GM(1,1)模型构建。
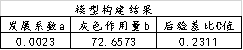
从上表可知,模型构建后得到发展系数a,灰色作用量b,发展系数a和灰色作用量b值为构建模型使用值,其实际意义较小。后验比C值;后验差比C值0.231 <=0.35,意味着模型精度等级非常好。如果要使用数学公式描述模型,如下所示即可:
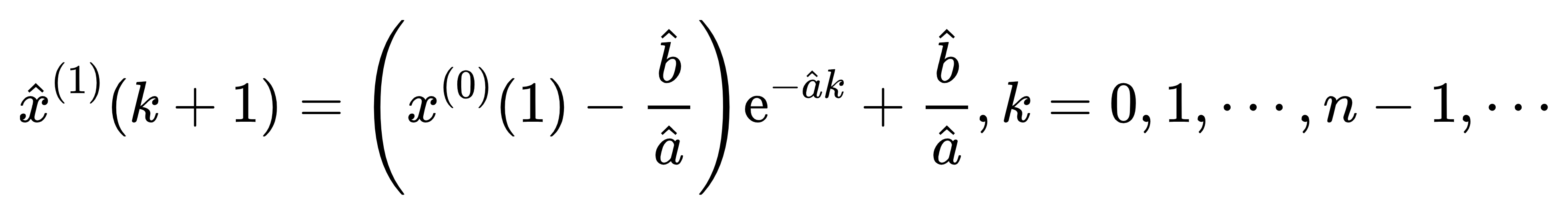
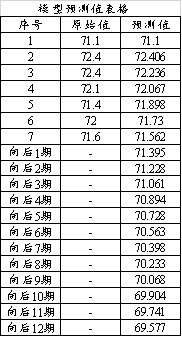
上表格展示出模型的拟合值,以及向后12期的拟合数据情况,当然也可通过图形直观查看如下图,下图明显可以看出,往后时会一直下降,这是GM(1,1)模型的特征,其仅适用于中短期预测,因此向后1期和向后2期的数据具有价值,更多的预测数据需要特别谨慎对待。

最后针对残差值进行检验,相对误差值越小越好,该值小于0.2说明达到要求,小于0.1说明达到较高要求;级比偏差值越小越好,该值小于0.2说明达到要求,小于0.1说明达到较高要求。
从上表可知,模型构建后可对相对误差和级比偏差值进行分析,验证模型效果情况;模型相对误差值最大值0.007 <0.1,意味着模型拟合效果达到较高要求。针对级比偏差值,该值小于0.2说明达到要求,若小于0.1则说明达到较高要求;模型相对误差值最大值0.020<0.1,意味着模型拟合效果达到较高要求。
6、剖析
涉及以下几个关键点,分别如下:
-
GM(1,1)模型仅适用于中短期预测,不建议进行长期预测;
-
GM(1,1)模型适用于数量少(比如20个以内)时使用,大量数据时不适合;
-
GM(1,1)模型有提供级比值检验,后验差比检验,模型残差检验等;并非所有检验均能完美,通常在可容忍范围内即可;
-
GM(1,1)模型构建共有四个步骤,分别是:第一步:级比值检验;第二步:后验差比检验;第三步:模型拟合和预测;第四步:模型残差检验。
疑难解惑
-
平移转换是什么意思?
-
灰色预测GM(1,1)模型时,数据通常需要满足级比值检验,如果不满足,且选中‘平移转换’时,SPSSAU默认会自动加入一常数c值,让数据满足级比值检验后再进行灰色预测分析。
-
级比偏差的计算公式?
-
针对灰色预测模型GM11,级比偏差的计算公式如下:级比偏差 = 1 - [( 1–0.5*a) / (1 +0.5*a)] * 对应的级比值λ,a为发展系数。
-
SPSSAU进行灰色预测gm11时RMSEA的计算?
-
RMSEA的意义为残差平方和的平均值并且开根号,即平均的残差值情况。在灰色预测gm11模型时,其第1项的残差值永远是0,因而第1项并不纳入RMSE指标计算。
-
RMSE、MSE、MAE和MAPE这4个指标分别什么意义?
-
RMSE(均方根误差),其表示模型拟合后的平均残差情况如何,即模型拟合后真实值与预测值之间的偏差有多大,该值越小越好;
-
MSE(均方误差),其表示模型拟合后的平均残差平方值如何,MSE开根号即为RMSE值,该值越小越好;
-
MAE(平均绝对误差),其为残差的绝对值之和,然后求平均值,其表示平均偏差是多大,与RMSE的意义基本一致,该值越小越好;
-
MAPE(平均绝对百分比误差),其为残差除以真实值的绝对值之和,然后求其平均。该值为相对指标值,其表示预测值与真实值之间gap平均偏离真实值的比例情况,比如为0.2,其表示平均偏离真实值20%左右,该值越小越好,并且该指标值具有比较意义,不同模型之间均可对比该值的相对大小,进而衡量模型优劣情况。
