模糊综合评价

模糊综合评价借助模糊数学的一些概念，对实际的综合评价问题提供评价，即模糊综合评价以模糊数学为基础，应用模糊关系合成原理，将一些边界不清、不易定量的因素定量化，进而进行综合性评价的一种方法。

举例来讲：某服装品牌生产某种服装新款式，欲了解消费者对该种款式的接受程度。一共有五个评价指标（分别是花色，式样，价格，耐用度，舒适度），以及评语共有四项（分别是很欢迎，欢迎，一般，不欢迎）。现在希望分析出消费者的综合评价情况如何，到底是很欢迎，还是欢迎，也或者一般或者不欢迎等。

上述例子中评价指标则为五项（花色，式样，价格，耐用度，舒适度），以及评语为四项（很欢迎，欢迎，一般，不欢迎）。如果说评价指标的权重不一样，此时则需要有指标权重指标值，也称作权重向量A（默认是五项的权重一样）。除此之外，消费者对于五项评价指标的评价打分情况（或者选择比例情况），我们称之为权重判断矩阵R。比如下表格：

指标项 很欢迎 欢迎 一般 不欢迎
花色 0.2 0.5 0.3 0.0
式样 0.1 0.3 0.5 0.1
价格 0.0 0.1 0.6 0.3
耐用度 0.0 0.4 0.5 0.1
舒适度 0.5 0.3 0.2 0.0

上表格展示出消费者对于五个评价指标的评语选择比例情况（当然表格中为选择个数也可以），比如针对价格，选择“很欢迎”的比例是0，但是选择一般的比例是0.6（即60%）。上述表格即称之为权重判断矩阵R，在使用SPSSAU操作时，直接拖拽“很欢迎”，“欢迎”，“一般”和“不欢迎”这四列进入分析框中即可。（当然上表中写成选择个数即数字也可以，SPSSAU会默认进行归一化处理，即将数字自动转化成百分数后进行计算）

如果说五项指标（花色，式样，价格，耐用度，舒适度）的权重不一样（默认是权重一样），此时可自行构评价指标权重向量A，比如下表：

指标项 指标项权重
花色 0.1
式样 0.1
价格 0.15
耐用度 0.30
舒适度 0.35

花色在评价体系中占的权重是0.1（即10%），而舒适度的权重是0.35（即35%）。（当然如果权重写成数字也可以，SPSSAU会默认进行归一化处理，即将数字自动转化成百分数后进行计算）【多数情况下，各项评价指标的权重均一致不需要单独处理】。

有了上述两个矩阵，即权重向量矩阵A和权重判断矩阵R；此时则可直接进行模糊综合评价权重计算，得出评价的综合情况，到底是是很欢迎，还是欢迎，也或者一般或者不欢迎等。以及也可以计算出综合得分，用于表示消费者的综合评价情况。

  • 综上所述：模糊综合评价共分为三个步骤，分别如下：

  • 第一步：确定评价指标和评语集；

  • 第二步：确定权重向量矩阵A和构造权重判断矩阵R；

  • 第三步：计算权重并进行决策评价。

  • 特别提示

  • 模糊综合评价共有四种计算方式（即四种模糊算子），SPSSAU默认推荐使用加权平均型这种综合最优的评价方式；

编号 模糊算子类型 说明
1 主因素突出型：M(Λ, V) 较少使用A矩阵和R矩阵信息，不推荐使用
2 主因素突出型：M(., V) 较少使用A矩阵和R矩阵信息，不推荐使用
3 加权平均型：M(Λ, +) 更多使用R矩阵信息，推荐使用
4 加权平均型：M(., +) 综合利用A矩阵和R矩阵信息，推荐使用

  • 关于权重向量矩阵A，如果不提供，SPSSAU默认会以所有指标的权重一致进行计算；如果提供，则按照提供的权重进行计算；

  • 关于权重向量矩阵A，无论如何，SPSSAU均需要先进行归一化处理，然后再进行计算；因此不论是数字还是小数均会得到正确的结果；

  • 关于权重判断矩阵R，无论如何，SPSSAU均需要先进行归一化处理，然后再进行计算；因此不论是数字还是小数均会得到正确的结果；

SPSSAU分析结果表格示例如下：

权重计算结果
很欢迎 欢迎 一般 不欢迎
隶属度 0.205 0.320 0.390 0.085
隶属度归一化【权重】 0.205 0.320 0.390 0.085
综合得分计算
综合得分 很欢迎 欢迎 一般 不欢迎
2.645 4 3 2 1

模糊综合评价案例

  • 1、背景

    某服装品牌生产某种服装新款式，欲了解消费者对该种款式的接受程度。一共有五个评价指标（分别是花色，式样，价格，耐用度，舒适度），以及评语共有四项（分别是很欢迎，欢迎，一般，不欢迎）。现在希望分析出消费者的综合评价情况如何，到底是很欢迎，还是欢迎，也或者一般或者不欢迎等。五个指标分别的权重为（0.1，0.1，0.15，0.3，0.35），以及消费者对于五个指标下四项评语的选择比例情况如下表所示，即原始数据格式如下表：

    指标项 指标项权重 很欢迎 欢迎 一般 不欢迎
    花色 0.1 0.2 0.5 0.3 0.0
    式样 0.1 0.1 0.3 0.5 0.1
    价格 0.15 0.0 0.1 0.6 0.3
    耐用度 0.3 0.0 0.4 0.5 0.1
    舒适度 0.35 0.5 0.3 0.2 0.0

    上表格显示：五个指标项均对应有权重，因此分析时需要将指标权重项放入分析框中；同时共有四项评语，则将四项评语放入分析框中。

    • 特别提示

    • SPSSAU分析时指标项的具体名称项（上表中第1列）不需要放入分析框中，当然SPSSAU也无法识别名字（智能分析会以“指标1”，“指标2”，“指标3”，“指标4”，“指标5”，分别表示花色，式样，价格，耐用度，舒适度这5项）

  • 2、理论

    完整的模糊综合评价分析法通常包括三个步骤，分别是：

    • 第一步：确定评价指标和评语集；

    • 第二步：确定权重向量矩阵A和构造权重判断矩阵R；

    • 第三步：计算权重并进行决策评价。

      此步骤中需要特别注意模糊算子的选择（即计算方式的选择），默认SPSSAU推荐使用加权平均型：M(., +)模糊算子，因此此计算方法综合利用了指标权重向量A和权重判断矩阵R的信息。

  • 3、操作

    本例子中共有四项评语（分别是很欢迎，欢迎，一般，不欢迎），并且五个评价指标的权重不一致，因而需要单独放置评价指标的权重矩阵A。SPSSAU操作截图如下：

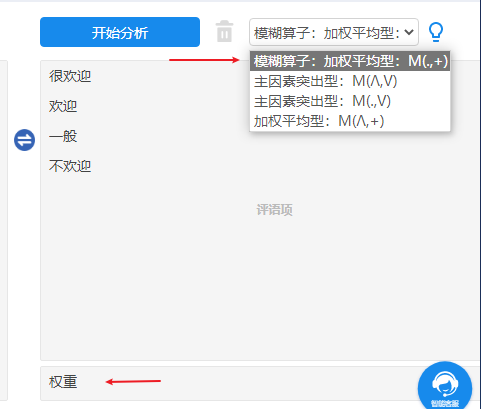
    • 特别提示：

    • 评价指标权重为“可选”，如果不放置，SPSSAU默认会以指标项权重相同进行处理（通常情况下均是此种情况）。

  • 4、SPSSAU输出结果

    权重计算结果
    很欢迎 欢迎 一般 不欢迎
    隶属度 0.205 0.320 0.390 0.085
    隶属度归一化【权重】 0.205 0.320 0.390 0.085

    上表格展示出综合评价情况，包括隶属度指标及权重（即隶属度归一化后数据），隶属度是用于判断综合评价应该放在具体某“评语”下面更合适的指标，根据最大隶属度法则，隶属度最大时对应的“评语”则为综合评价的结果。

    隶属度归一化，即对隶属度进行归一化处理，计算得出的权重。

    综合得分计算
    综合得分 很欢迎 欢迎 一般 不欢迎
    2.645 4 3 2 1

    如果说希望得到一个综合得分，用于描述评价综合情况，用于进行多个评价体系进行对比等，则可以使用综合得分计算表格。不同的评语有着不同的分值，因此输入评语的分值后就会得出综合得分【综合得分是利用隶属度归一化即权重度与评语分值进行加权得出】。

  • 5、文字分析

    权重计算结果
    很欢迎 欢迎 一般 不欢迎
    隶属度 0.205 0.320 0.390 0.085
    隶属度归一化【权重】 0.205 0.320 0.390 0.085

    从上表可知，针对5个指标(指标1, 指标2, 指标3, 指标4, 指标5)【样本量为5所以有5个指标】,以及4个评语集进行模糊综合评价，并且使用M(., +)算子进行研究；

    • 特别提示

    • SPSSAU分析时指标项的具体名称无法识别，因而以“指标1”，“指标2”，“指标3”，“指标4”，“指标5”等进行代替（此处实际意义分别对应为：花色，式样，价格，耐用度，舒适度）。

    首先建立评价指标权重向量矩阵A，以及构建出5x4权重判断矩阵R，最终进行分析出4个评语集的权重值，分别是：0.205,0.320,0.390,0.085。4个评语集中一般的权重值最高(0.390)，结合最大隶属度法则可知，最终综合评价结果为属于一般。

    同时从上表格可以看出，综合来看有39%的消费者选择“一般”，还有32%的消费者选择“欢迎”。

    综合得分计算
    综合得分 很欢迎 欢迎 一般 不欢迎
    2.645 4 3 2 1

    结合实际情况，针对四个评语（很欢迎，欢迎，一般，不欢迎），分别赋分为4，3，2和1分；然后计算得出综合得分值是2.645分。综合得分介于“欢迎”和“一般”之间。

  • 6、剖析

    • 特别提示

    • 关于权重向量矩阵A，如果不提供，SPSSAU默认会以所有指标的权重一致进行计算；如果提供，则按照提供的权重进行计算；

    • 关于权重向量矩阵A，无论如何，SPSSAU均需要先进行归一化处理，然后再进行计算；因此不论是数字还是小数均会得到正确的结果；

    • 关于权重判断矩阵R，无论如何，SPSSAU均需要先进行归一化处理，然后再进行计算；因此不论是数字还是小数均会得到正确的结果；

    • 请特别注意数据格式的上传及操作；

    • SPSSAU分析时指标项的具体名称无法识别，智能分析会以“指标1”，“指标2”，“指标3”，“指标4”，“指标5”等进行代替。

疑难解惑

  • 简要概述模糊综合评价是什么?

  • 模糊综合评价是一种综合评价方法，其涉及到4个关键术语名词，分别是：指标项、评语、权重判断矩阵R、权重向量矩阵A，分别如下说明：

  • 指标项：比如对于Iphone手机在3个方面的满意度，价格满意度、样式满意度和IOS系统满意度；

  • 评语：指标项的‘选项’，比如非常满意，满意，一般，不满意等；模糊综合评价即用来判断最终到底应该属于那个评语项；

  • 权重判断矩阵R：指标项及各评语的选择频数（或者比例），即需要上传的原始数据；

  • 权重向量矩阵A：如果Ipone手机3个方面满意度的权重不一样，则需要设置，如果权重一样则不需要处理。

  • 上传数据格式如何?

  • 模糊综合评价需要上传的数据即为权重判断矩阵R，格式很特殊，类似如下表所示：

指标项 非常满意 满意 一般 不满意
价格满意度 30 25 4 5
样式满意度 20 23 10 11
IOS系统满意度 40 21 1 2

  • 上表格即为需要上传的原始数据格式（3个指标项，4个评语），里面的数字换成百分比也可以（数字代表某指标项在某评语上的选择个数），同时数字需要手工整理好，通常可使用比如频数分析得到，然后自行整理规范后上传即可。

  • 上传后将四个评语拖拽到‘右侧框’中即可进行分析。

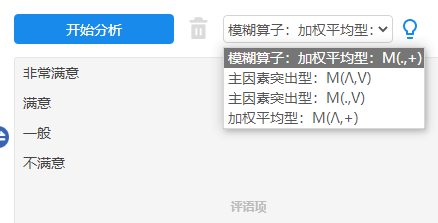
  • 三级指标有数据，二级指标如何计算权重？

  • 如果是层次结构的数据进行模糊综合评价。比如有3个二级指标分别是A,B,C；A对应着A1,A2,A3; B对应着B1,B2,B3,B4; C对应着C1,C2,C3,C4；那么A1,A2,A3进行一次模糊综合评价；B1,B2,B3,B4进行一次模糊综合评价；C1,C2,C3,C4进行一次模糊综合评价。A,B,C如果没有数据，则无法单独进行模糊综合评价；可考虑将所有三级指标数据全部一起进行一次模糊综合评价，然后借助“隶属度归一化【权重】”值进行分析。

  • SPSSAU 模糊综合评价时如何使用综合得分？

  • 模糊综合评价时，首先会计算出权重值，然后研究者可输入指标项的分值，则会得到综合得分值，其计算原理为指标项分值与权重值相乘后累加。一般情况下并不需要使用综合得分，其意义频率较低。

  • 模糊综合评价时隶属函数是什么意思？

  • 模糊综合评价时，结合隶属函数可计算得到隶属度，具体分别如下：

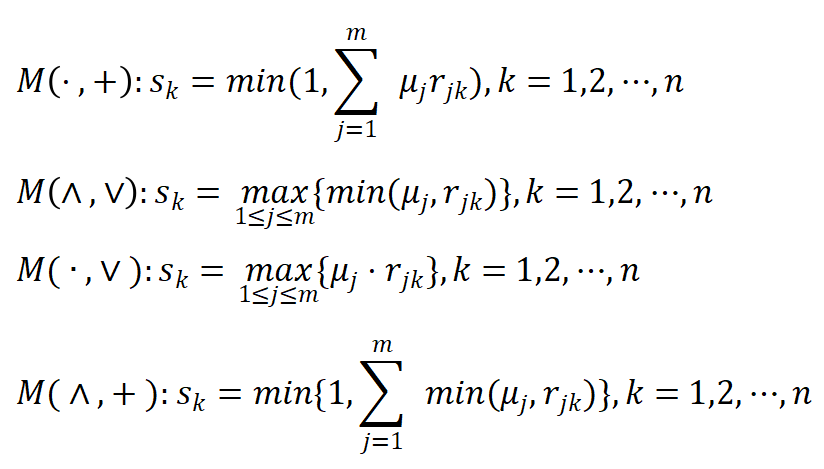
  • SPSSAU进行模糊综合评价时数据格式如何？

  • 模糊综合评价时其数据格式可参考本页面案例，或者SPSSAU数据格式页面：点击查看。