模糊层次分析法FAHP
-
案例数据下载 下载
模糊层次分析法FAHP(Fuzzy Analytic Hierarchy Process),其是在传统层次分析法(AHP)的基础上,结合模糊集理论发展而来的一种多准则决策方法。其结合层次分析法和模糊集理论,其可用于处理决策问题中不确定性和模糊性,通常在实际应用中可用于权重计算也或者排序等,比如评估供应商的重要性进而进行选择,项目风险评估,各类影响评价和相关决策辅助等。一般来说,FAHP的分析包括几个步骤分别是:建立模型互补矩阵,计算好模糊权重和模糊一致性检验等。
模糊层次分析法FAHP
-
1、背景
当前有一份关于选择供应商选择的四个评价指标,该四个评价指标有着相对重要性数据,希望通过对评价指标的权重计算,进而结合各供应商在四个评价指标上的实际得分并且乘上权重求和,得到综合得分,进而对各供应商的优先级进行评估。当然关于四个评价指标的相对重要性数据如下:
指标1 指标2 指标3 指标4 0.5 0.7 0.6 0.7 0.3 0.5 0.6 0.6 0.4 0.4 0.5 0.6 0.3 0.4 0.4 0.5 -
表格中数据展示各指标的重要性情况,其为原始数据,在数学上也称作模糊互补矩阵(R矩阵,也称模糊判断矩阵)。其特点如下:
-
模糊互补矩阵为n*n阶格式,数字表示相对重要程度,其介于0.1 ~ 0.9之间,数字越大表示越重要;
-
模糊互补矩阵其右下三角线为0.5 ,表示自己与自己同等重要;
-
比如上表格中指标1相对指标4为0.7,其表示指标1相对指标4更加重要,那么指标4相对指标1则为相对不那么重要为0.3,其对称的两个值相加一定为1。
-
-
2、理论
-
模糊层次分析法FAHP时包括以下几个计算步骤,分别如下:
-
准备好模糊判断矩阵;
-
利用模糊判断矩阵计算权重,并且得到归一化权重,权重计算公式如下:
上式中n为矩阵阶数,比如本案例为4个指标即4阶。aij表示第i和第j项模糊判断矩阵数据。上式可直接计算得到权重值,最后对权重进行归一化处理即得到归一化权重值。
-
计算特征矩阵;
特征矩阵计算公式为Wij=Wi / (Wi + Wj), Wi或Wj表示第i或j个指标的权重值。计算特征矩阵的目的是进行一致性检验。
-
一致性检验;
通过相容性CR指标进行检验模糊一致性,CR值<0.1则认为通过模糊一致性检验,反之则不通过。CR指标的计算上,其是利用模糊互补矩阵(即原始数据)与特征矩阵进行计算得到,其计算公式为:
上式中,A表示模糊互补矩阵,W为特征矩阵,n为阶数。
-
-
3、操作
本例子SPSSAU操作如下:
将模糊互补矩阵数据粘贴(或编辑)到表格中,然后点击开始分析即可。
-
4、SPSSAU输出结果
SPSSAU共输出5个表格和1个权重分布图,如下说明。
表格 说明 模糊互补R矩阵 即原始放入的数据 数据标度表格 展示具体数据的相对重要性情况即标度说明 FAHP权重结果 展示权重及归一化后权重 特征矩阵 展示特征矩阵数据 一致性校验 展示CR指标及一致性检验结果 -
5、文字分析
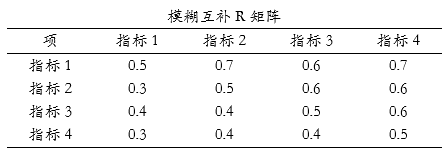
上表格为模糊互补R矩阵,其输入的原始数据。并且在下表格中展示数据标度,即模糊互补R矩阵中数字的大小意义。比如指标1与指标4时为0.7,其意味着指标1相对于指标4显得‘明显重要’,当然反过来指标4比指标1会‘明显不重要’,其值为1-0.7=0.3。模糊互补R矩阵一定是对称两个值加和为1,并且主对角线上的数据为0.5,因为自己与自己为同等重要的意思。


上表格为最权重结果,包括归一化之前和归一化之后,通常情况下是看归一化之后的权重值,因为归一化前的权重数据加和很可能不等于1。
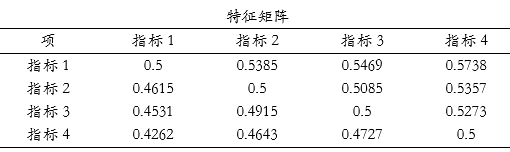
上表格展示特征矩阵数据,其并没有特别意义。目的是进行一致性检验时使用到,其对角线值也全部为0.5。

上表格一致性检验结果,上表格显示相容性一致性检验指标CR值为0.0712<0.1,因而意味着通过一致性检验,如果没有通过一致性检验,需要考虑是否有出现比如指标1相对指标2更加重要,指标2比起指标3更加重要,那么肯定指标1相对指标3更重要,但数据上却出现指标3比指标1更重要。
-
6、剖析
-
涉及以下几个关键点,分别如下:
-
请确保提供正确的模糊互补矩阵,其数字表示相对重要程度,其介于0.1 ~ 0.9之间,数字越大表示越重要,模糊互补矩阵其右下三角线为0.5 ,表示自己与自己同等重要。
-
FAHP的计算公式参考文献如下:张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学, 2000.DOI:CNKI:SUN:MUTE.0.2000-02-015.
-
-
7、疑难解惑
-
FAHP分析时一致性检验没有通过?
-
如果没有通过一致性检验,需要考虑是否有出现比如指标1相对指标2更加重要,指标2比起指标3更加重要,那么肯定指标1相对指标3更重要,但数据上却出现指标3比指标1更重要。
-