P-P图和Q-Q图常用于直观查看数据是否正态分布。P-P图和Q-Q图的目的性基本一致,但原理上有着区别。
针对P-P图,其原理在于如果数据正态,那么数据的累积比例与正态分布累积比例基本保持一致。分别计算出数据累积比例,和假定正态时的数据分布累积比例;并且将实际数据累积比例作为X轴,将对应正态分布累积比例作为Y轴,作散点图。
针对Q-Q图,其原理在于如果数据正态,那么其假定的正态分位数会与实际数据基本一致。计算出假定正态时的数据分位数;并且将实际数据作为X轴,将假定正态时的数据分位数作为Y轴,作散点图。
无论是P-P图,或者Q-Q图;如果说数据呈现出正态性,那么散点图看上去应该近似呈现为一条对角直线,此时说明数据呈现出正态性。如果散点图看上去明显不是一条直线,那么说明数据很可能不具有正态特质。P-P图和Q-Q图的功能一致,使用时并没有区别,看使用偏好选择即可。
-
P-P图和Q-Q图的通常均用于数据正态性查看,常见使用场景如下:
-
方差分析(包括普通单因素方差,双因素方差,三因素方差,多因素方差,协方差分析等),对应的Y值是否具有正态性特质的判断;
-
回归分析(包括线性回归,逐步回归等)前,对应的Y值是否具有正态性特质判断;回归分析(包括线性回归,逐步回归等)后,使用P-P图和Q-Q图检查残差值是否有正态性特质;
-
二元Logit回归后的残差值是否有正态性特质。
-
其它用于直观展示数据正态性的场景。
-
SPSSAU特别提示:
-
正态性检验有多种方法:包括使用统计检验方法,作图法等;
-
使用统计检验方法进行正态性查看时,很容易被判断为非正态性分布,建议使用作图法(包括P-P图,Q-Q图,柱形图带正态分布曲线)进行查看;
-
绝对的正态性生活中几乎不会出现,数据接近于正态分布更加符合实际情况;
-
正态性检验是针对定量数据,而且是连续的定量数据,比如身高、体重这一类数据。
-
经典的研究方法(比如方差分析)要求数据呈现出正态性特质;如果不满足正态性则可考虑使用非参数检验。但在实际研究中,数据很难出现绝对的正态性【理论和实际数据会有‘代勾’】,并且由于研究方法的稳健性,因而即使数据正态特质较少,很多时候依然使用对应的研究方法(要求正态性这一前提的研究方法)。
-
下表格列出,数据正态和不正态时使用的常见研究方法对比:
| 编号 | 定量数据呈现正态性 | 定量数据非正态性 |
|---|---|---|
| 1 | 方差(单因素) | 非参数检验(包括MannWhitney或者Kruskal-Wallis检验) |
| 2 | t 检验(独立t 检验) | 非参数检验(MannWhitney检验) |
| 3 | 单样本t 检验 | Wilcoxon符号秩 |
| 4 | 配对t 检验 | Wilcoxon符号秩 |
| 5 | Pearson相关系数 | Spearman相关系数 |
SPSSAU输出P-P图说明:
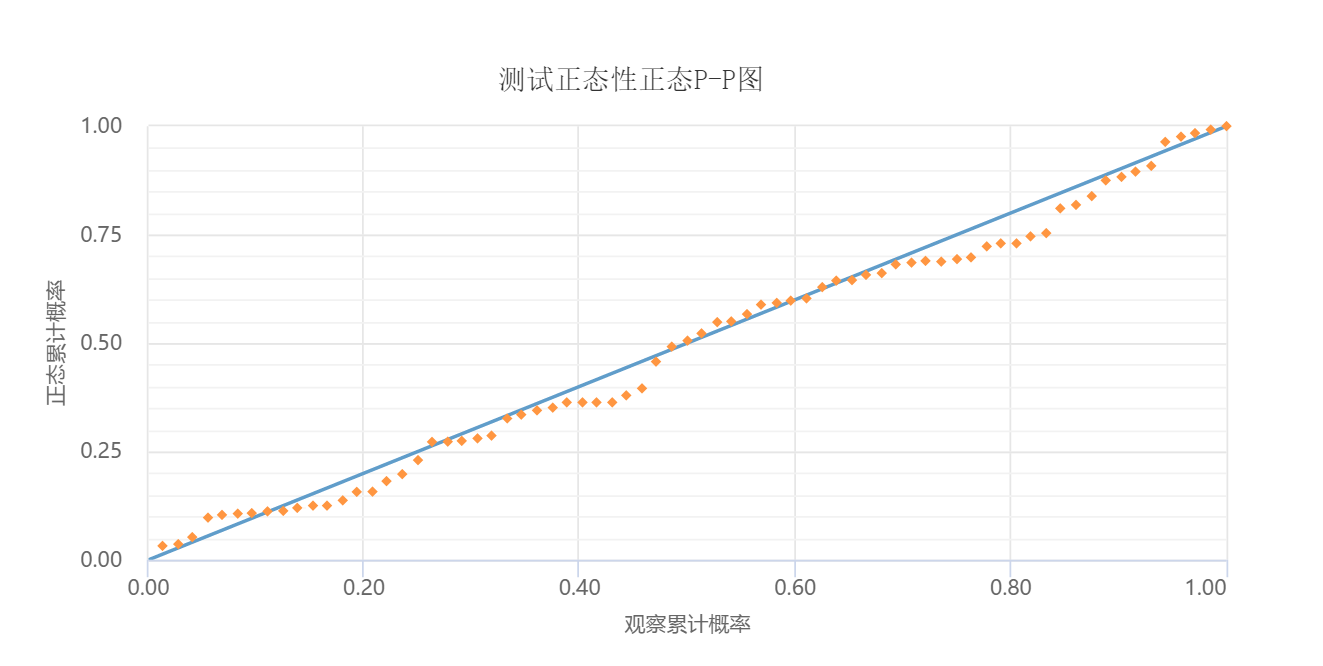
-
上图是回归分析保存的残差值作P-P图,用于检测残差是否满足正态性,上图可以看出,数据基本上呈现出一条对角直线,也即意味着残差服从正态性分布特质。
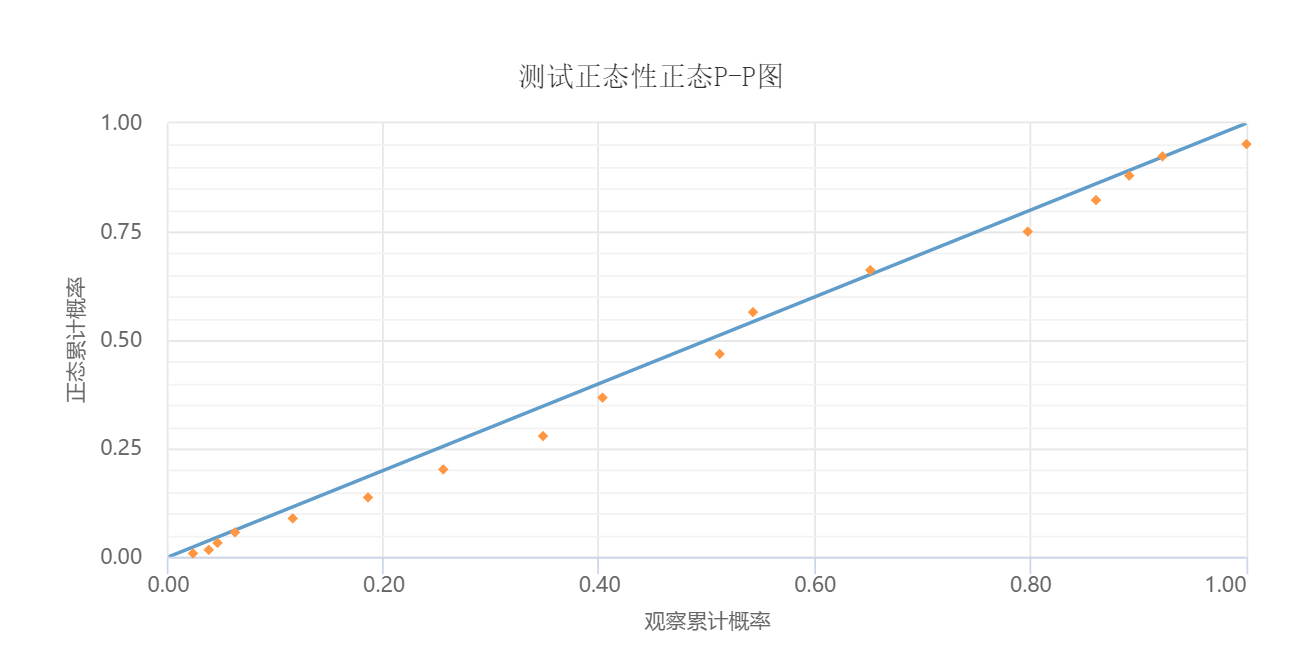
-
上图可以看出,数据基本上呈现出一条对角直线,但也有较多的点并不在直线上, 只是接近在直线上,因而说明数据基本上满足正态性特质,可以接受。
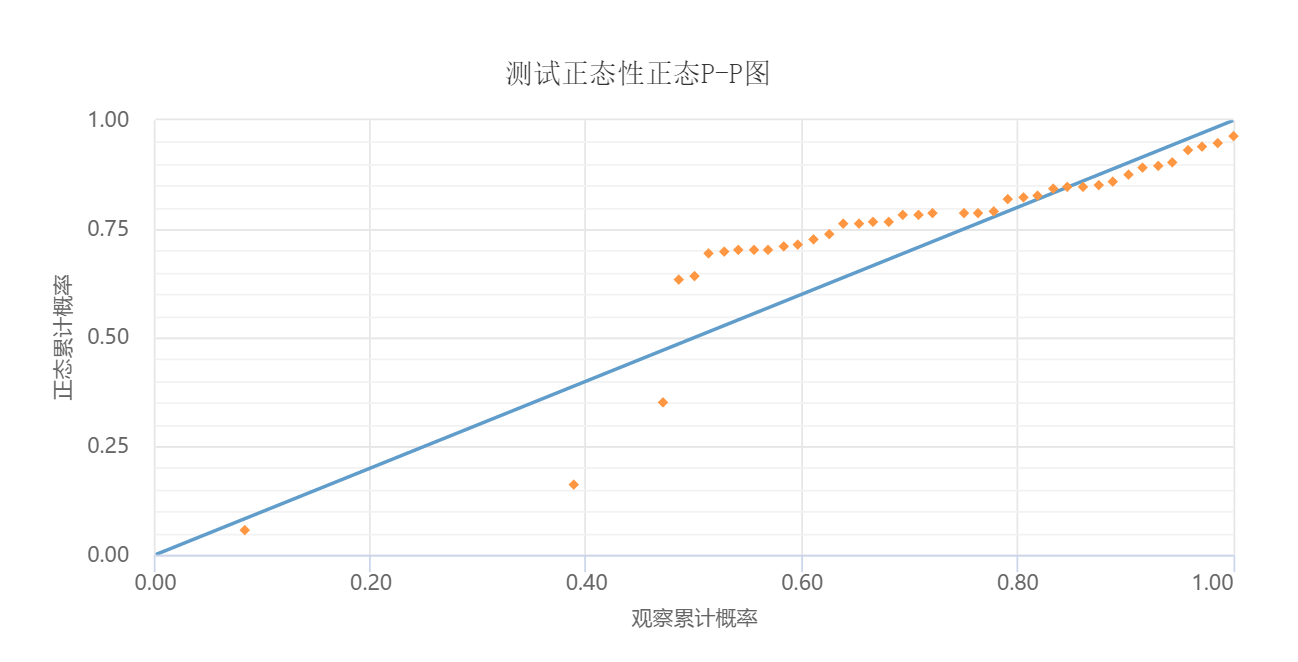
-
上图可以看出,数据中较多的点并不在直线上,因而说明数据不太满足正态性特质。
