方差分析

  • 方差分析(单因素方差分析),用于分析定类数据与定量数据之间的关系情况.例如研究人员想知道三组学生的智商平均值是否有显著差异.方差分析可用于多组数据,比如本科以下,本科,本科以上共三组的差异;而下述t 检验仅可对比两组数据的差异

    • 首先判断p 值是否呈现出显著性,如果呈现出显著性,则说明不同组别数据具有显著性差异,具体差异可通过平均值进行对比判断.

    分析项 方差分析说明
    学历,网购满意度 不同学历的人群,他们网购满意度是否有差异?

  • 分析结果表格示例如下(SPSSAU同时会生成折线图等):

    学历(平均值±标准差) F p
    本科以下(n=67) 本科(n=53) 硕士及以上(n=28)
    分析项1 3.23±1.33 2.88±0.73 2.63±0.81 3.73 0.03*
    分析项2 2.62±1.48 2.57±1.21 2.32±0.76 0.56 0.58
    分析项3 2.14±1.10 2.16±0.76 2.25±0.95 0.13 0.88
    分析项4 3.31±1.12 3.32±1.02 3.82±0.85 2.67 0.07
    分析项5 3.75±1.06 3.56±0.80 3.82±0.76 0.97 0.38
    * p <0.05 ** p <0.01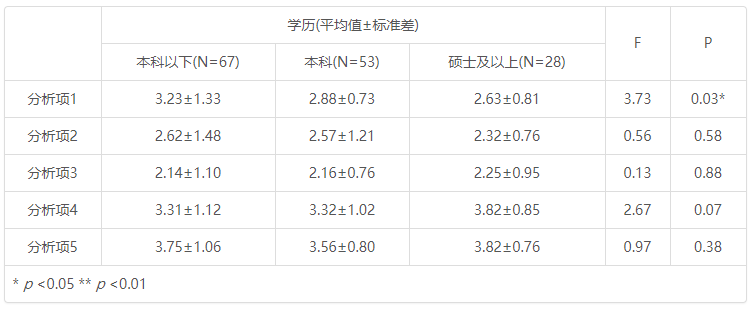
    • 特别提示

    • 方差分析，t 检验和交叉(卡方)，共三个分析方法，均是对比差异性。

    三个方法的区别如下：

    X数据类型 X组别 Y 分析方法
    定类 2组或者多组 定量 方差
    定类 仅仅2组 定量 t 检验
    定类 2组或者多组 定类 卡方

    SPSSAU操作截图如下：

    • 特别提示

    • 如果希望进行方差齐检验，可以在复选框中选择即可

方差分析案例

  • 1、背景

    当前有一份数据,有基本信息，比如性别和学历等。想研究不同背景人群对“淘宝客服服务态度”，“淘宝商家服务质量”，这两项的差异性，“淘宝客服服务态度”，“淘宝商家服务质量”这两项均是定量数据，因而可使用方差分析，通过平均值进行差异性对比。

  • 2、理论

    方差分析（ANOVA）有很多种类型，最普遍的是单因素方差，即研究X对于Y的差异性，其中X为定类数据，Y为定量数据。方差分析最终分析时，首先分析p 值，如果此值小于0.05，说明呈现出差异性；具体差异再对比平均值即可。如果p 值大于0.05则说明没有差异性产生。F 值属于中间过程值，想要计算p 值，一定要先计算F 值，因而SPSSAU也将F 值结果输出。

    • 特别提示

    • 如果X和Y均为定类数据，想对比差异性，此时需要使用卡方分析。

    • 如果X为定类，Y为定量；且X分为两组，比如男和女；此时也可使用t 检验进行差异对比(当然也可使用方差分析)。

    • 关于方差齐和方差的关系

    • 理论上讲，方差分析前需要满足方差齐，如果方差齐则使用方差分析，如果方差不齐则使用非参数检验。

    • 理论和实践相比，永远有gap，现实研究中，最常见的依然是方差分析（而不是非参数检验），原因在于非参数检验的检验效能相对于方差分析会低一些。

  • 3、操作

    • 本例子中研究X对于Y的差异；X为学历，Y为两项，分别是“淘宝客服服务态度”，“淘宝商家服务质量”。放置如下：

  • 4、SPSSAU输出结果

    学历(平均值±标准差) F p
    本科以下(n=40) 本科(n=88) 本科以上(n=72)
    淘宝客服服务态度 3.44±0.625 3.86±0.48 4.58±0.50 69.38 0.00**
    淘宝商家服务质量 3.53±0.64 3.92±0.49 4.58±0.61 49.70 0.00**
    * p <0.05 ** p <0.01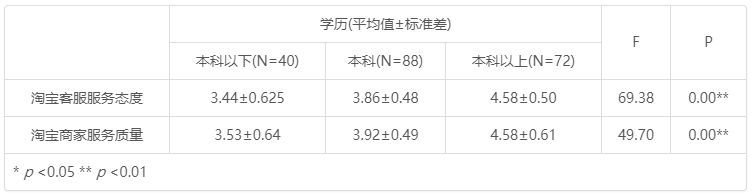

    共输出F 值和p 值，以及还有平均值与标准差值。p 值和平均值才更有意义；但需要输出F 值和标准差值，原因在于p 值需要通过F 值计算得到，以及原理上是否有差异会与标准差值有关联性。

  • 5、文字分析

    • 使用方差分析去研究学历分别与“淘宝客服服务态度”，“淘宝商家服务质量”这两项的差异关系，结果显示，不同学历群体样本对于“淘宝客服服务态度”，“淘宝商家服务质量”均呈现出显著性差异(p <0.05)。具体对比可知：

    • 不同学历人群对于“淘宝客服服务态度”呈现出0.01水平的显著性差异差异态度(F =69.38,p =0.00 <0.01）,具体通过平均值对比差异可知：相对来看，学历越高的样本人群，他们对于“淘宝客服服务态度”的认可态度会越高。

    • 不同学历人群对于““淘宝商家服务质量”” 呈现出0.01水平的显著性差异(F =49.70,p =0.00 <0.01）,具体通过平均值对比差异可知：相对来看，学历越高的样本人群，他们对于““淘宝商家服务质量””的认可态度会越高。

    • 特别提示

    • 学历共有三组，分别是本科以下，本科和本科以上；而且p 值小于0.05，具体是那两个组别之间的差异导致学历有差异呢？如果想知道此信息，可使用事后多重比较分析方法进行研究。

  • 6、剖析

    方差分析涉及以下几个关键点，分别如下：

    • 本例中本科以下共40人，本科88人，本科以上72人。如果说本科以下仅10人，那么10个人通常没有什么代表意义，可以考虑将本科以下和本科合并成一组；需要使用到SPSSAU的数据编码功能。

    • 方差分析显示p 值小于0.05时，可考虑使用事后多重比较。

    • 方差不齐时可考虑使用非参数检验，但如果是问卷研究，依然使用方差分析的情况较多。：

    • 如果X仅为两组，比如本科及以下，本科以上；此时也可使用t 检验进行差异对比（选择使用即可，并没有特别要求）

疑难解惑

  • 出现null或者0.00

  • 有时候会出现“null”的结果，原因在于该类别的样本量为1，所以无法计算标准差值出现null，建议使用“数据处理->数据编码”功能对组别进行合并，然后再分析。

  • 有时候会出现“0.00”的结果，原因在于如果某类别的数字完全相同则会出现标准差值为0.00。

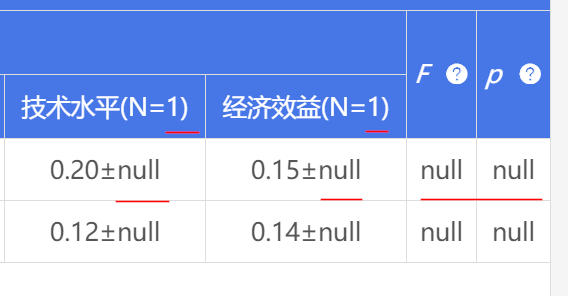
  • 针对问卷量表数据，几个题表示一个维度，如何处理？

  • 比如有两个题“我愿意向朋友推荐SPSSAU”，“我有需要会再来使用SPSSAU”，此两个题是“忠诚度”的体现。但现在需要“忠诚度”这个整体，而不是具体两个标题，此时如何办呢？

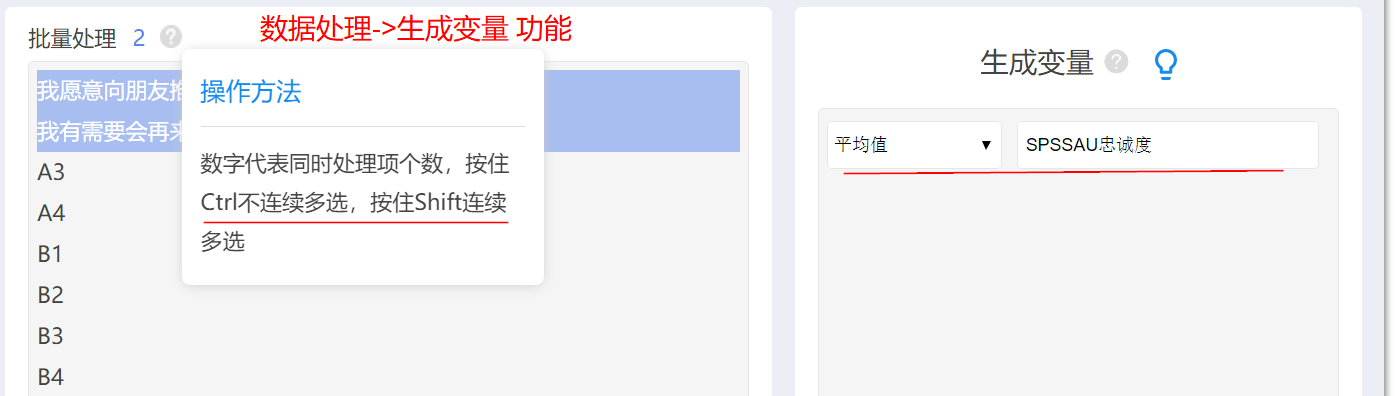
  • 方差分析是否需要满足正态性？

  • 从理论上讲，方差分析有两个前提条件，一是因变量Y需要满足正态性要求，二是满足方差齐检验。如果不满足，此时可使用【通用方法->非参数检验】进行研究差异性。也有文献提及可将数据进行转换后使其更加接近或符合正态性，然后继续使用方差分析，用户可尝试进行数据转换【数据处理->生成变量】功能，一般是对数据进行比如求对数，开根号等处理。理论上的正态分布并不存在，数据接近于正态分布更符合实际情况，因此接近正态分布的数据直接使用方差分析即可。

  • 方差分析是否需要满足方差齐？

  • 从理论上讲，方差分析有两个前提条件，一是因变量Y需要满足正态性要求，二是满足方差齐检验。如果不满足，此时可使用【通用方法->非参数检验】进行研究差异性。但一般来讲如果不满足方差齐条件，检验性能也较好，因而多数时候并没有进行方差齐检验直接就使用方差分析。

  • 方差分析需要的数据格式?

  • 1.方差分析是研究X对于Y的影响，X是定类数据代表组别，Y是定量数据；有时候会出现只有Y但没有X的现象，比如有三个Y，分别是“服务满意度”、“快递满意度”和“价格满意度”，现在想对比3个满意度的差异性。此时就只有3个Y，但没有X，因此需要数据处理后才能进行方差分析；

  • 2.具体处理为，在EXCEL中单独加一列表示组别，然后把Y的数据重叠成一列称作“满意度”（比如有50个样本即50行数据，则重叠变成150行），相对于研究3组数据的差异性（X组别中数字1表示“服务满意度”，数字2表示“快递满意度”，数字3表示“价格满意度”），类似如下图：

X组别 Y满意度
1 3.45
1 4.32
2 3.25
2 3.67
3 3.98
3 3.76
  • 关于效应量(effect size)说明?

  • 当呈现出显著差异性(前提)时,可分析差异,同时还可以分析差异幅度(即效应量) (提示:效应量分析为可选，只有深入研究时才需要分析);

  • 方差分析时,通常使用Eta方表示效应量,其计算公式为: 偏Eta方=SSB/SST，SSB和SST均为中间过程值无需关注，SSB表示组间差，SST为总差异;

  • 偏Eta方值介于0~1之间，该值越大说明差异幅度越大，比如偏Eta方为0.1，即说明数据的差异有10%是来源于不同组别之间的差异，一般情况下偏Eta值非常小，使用偏Eta方表示效应量大小时，效应量小、中、大的区分临界点分别是:0.01，0.06和0.14；

  • 同时还可以使用Cohen’s f 表示效应量，其计算公式为:Sqrt(偏Eta方 / (1 - 偏Eta方))，Sqrt指开根号；Cohen’s f 表示效应量大小时，效应量小、中、大的区分临界点分别是:0.10，0.25和0.40。

  • 方差不齐时如何办？

  • 方差不齐时可使用‘非参数检验’，同时还可使用welch 方差，或者Brown-Forsythe方差，非参数检验是避开方差齐问题；而welch方差或Brown-Forsythe方差是直面方差齐，即使在方差不齐时也保证结果比较稳健，welch方差和Brown-Forsythe方差仅在计算公式上不一致，目的均是让方差不齐时结果也稳健，选择其中一种即可。

  • 方差分析中间过程值，组间平方和、组内平方和、自由度、均方等问题？

  • 方差分析用于研究差异，差异共由两部分组成，分别是组间平方和，组内平方和；

  • 同时对应着自由度值等；计算分别如下：

  • 组间自由度df 1=组别数量 – 1；

  • 组内自由度df 2 = 样本量 – 组别数量；

  • 组间均方 = 组间平方和 / 组间自由度df 1；

  • 组内均方 = 组内平方和 / 组内自由度df 2；

  • F 值 = 组间均方 / 组内均方；

  • p 值是结合F 值，df 1和df 2计算得到。

  • 方差分析结果中出现null值？

  • 如果说某类别的数据标准差为0为null值，此时进行方差分析或方差齐检验，Welch方差或Brown-Forsythe方差时，均可能导致计算不出相关指标。建议分析前先使用数据处理->数据编码功能对组别进行合并，然后再进行分析。