-
方差齐检验,用于分析不同定类数据组别 对 定量数据时的波动情况是否一致.例如研究人员想知道三组学生的智商 波动情况是否一致(通常情况希望波动一致,即方差齐)。
-
首先判断p 值是否呈现出显著性(p <0.05),如果呈现出显著性,则说明不同组别数据波动不一致,即说明方差不齐;反之p 值没有呈现出显著性(p >0.05)则说明方差齐。
分析项 方差分析说明 学历,身高 不同学历的人群,他们身高波动情况是否有区别? -
-
分析结果表格示例如下:
学历(标准差) F p 本科以下(n=67) 本科(n=53) 硕士及以上(n=28) 身高 1.33 0.73 0.81 3.73 0.03* * p <0.05 ** p <0.01 -
特别提示
-
方差齐是方差分析的前提,如果不满足则不能使用方差分析。
类型 使用方法 研究X(定类)对Y(定量)的差异性 Y方差齐 方差分析 研究X(定类)对Y(定量)的差异性 Y方差不齐 非参数检验或Welch方差或Brown-Forsythe方差 -
备注说明:
-
方差不齐时可使用‘非参数检验’,同时还可使用welch 方差,或者Brown-Forsythe方差,非参数检验是避开方差齐问题;而welch方差或Brown-Forsythe方差是直面方差齐,即使在方差不齐时也保证结果比较稳健,welch方差和Brown-Forsythe方差仅在计算公式上不一致,目的均是让方差不齐时结果也稳健,选择其中一种即可。
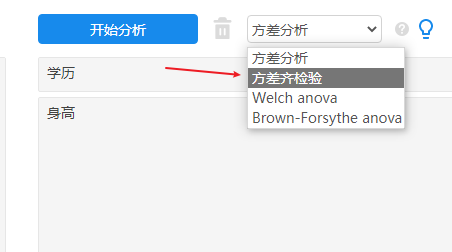
SPSSAU操作截图如下:
-
