-
相关分析用于研究定量数据之间的关系情况,包括是否有关系,以及关系紧密程度等.此分析方法通常用于回归分析之前;相关分析与回归分析的逻辑关系为:先有相关关系,才有可能有回归关系。
-
用户可自由拖拽分析项进入分析列表框,区别仅在于输出格式不同。
-
相关分析使用相关系数表示分析项之间的关系;首先判断是否有关系(有*号则表示有关系,否则表示无关系);
-
接着判断关系为正相关或者负相关(相关系数大于0为正相关,反之为负相关);
-
最后判断关系紧密程度(通常相关系数大于0.4则表示关系紧密);
-
相关系数常见有两类,分别是Pearson和Spearman,本系统默认使用Pearson相关系数。
-
在相关分析之前,SPSSAU建议可使用散点图直观查看数据之间的关系情况。除此之外,SPSSAU还提供Kendall相关系数。三个相关系数的区别如下表格:
系数 使用场景 备注 Pearson 定量数据,数据满足正态性时 PP/QQ图,直方图均可查看正态性,也或者使用正态性检验(检验最严格); Spearman 定量数据,数据不满足正态性时 PP/QQ图,直方图均可查看正态性,也或者使用正态性检验(检验最严格); Kendall 定量数据一致性判断 通常用于评分数据一致性水平研究【非关系研究】,比如评委打分,数据排名等。 分析项 相关分析说明 网购满意度,重复购买意愿 网购满意度和重复购买意愿之间是否有关系,关系紧密程度如何? -
特别提示
-
如果多个量表题表示一个维度,可使用“生成变量”的平均值功能。将多个量表题合并成一个整体维度。
-
-
分析结果表格示例如下
格式1(当仅放入一个框中时):
平均值 标准差 分析项1 分析项2 分析项3 分析项4 分析项5 分析项1 3.43 0.76 41.4 1 分析项2 3.93 0.86 .673** 1 分析项3 3.84 0.90 .740** .712** 1 分析项4 3.32 1.01 .681** .705** .642** 1 分析项5 3.03 1.09 .520** .666** .489** .604** 1 * p <0.05 ** p <0.01 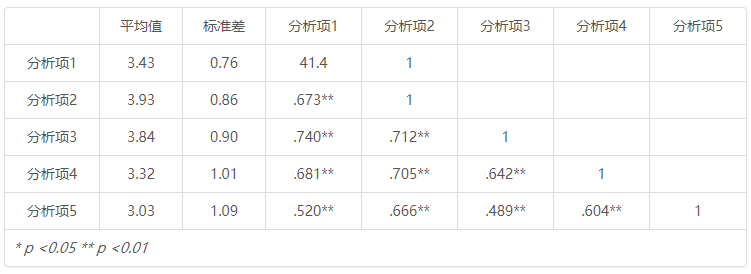
-
格式2(两个框均放置项时):
分析项1 分析项2 分析项3 分析项4 .641** .705** .242** 分析项5 .520** .656** .589** 分析项6 .321** .875** .242** 分析项7 .611** .705** .342** 分析项8 .530** .826** .589** * p <0.05 ** p <0.01 -
特别提示
-
通常情况下会使用格式1,如果希望格式2,则右侧两个框中均需要放置分析项。单从相关分析方法角度看,其并不区分X和Y,但从实际意义上看,通常是研究X和Y的相关关系。
SPSSAU操作截图如下(格式1):
SPSSAU操作截图如下(格式2):
-
相关分析案例
-
1、背景
比如想研究“淘宝客服服务态度”,“淘宝商家服务质量”分别与“淘宝商家满意度”,“淘宝忠诚度”之间的关系情况,此句话中明显的可以看出“淘宝客服服务态度”,“淘宝商家服务质量”这两项为 X;而“淘宝商家满意度”,“淘宝忠诚度”这两项为 Y。
-
特别提示
-
从分析方法角度,相关分析并不区分X或者Y;但是从分析思路角度建议区分X或者Y。
-
如果“淘宝客服服务态度”由几个题项表示,此时可使用“生成变量”->“平均值”功能,将几项概括成一个整体。
-
-
2、理论
相关分析是研究两个定量数据之间的相关关系情况,以及相关分析是研究有没有关系。
-
如果呈现出显著性(结果右上角有*号,此时说明有关系;反之则没有关系);有了关系之后,关系的紧密程度直接看相关系数大小即可。一般0.7以上说明关系非常紧密;0.4~0.7之间说明关系紧密;0.2~0.4说明关系一般。
-
如果说相关系数值小于0.2,但是依然呈现出显著性(右上角有*号,1个*号叫0.05水平显著,2个*号叫0.01水平显著;显著是指相关系数的出现具有统计学意义普遍存在的,而不是偶然出现),说明关系较弱,但依然是有相关关系。
-
相关分析是回归分析的前提条件,首先需要保证有相关关系,接着才能进行回归影响关系研究。
-
因为如果都显示没有相关关系,是不可能有影响关系的。
-
如果有相关关系,但也不一定会出现回归影响关系。
-
特别提示
-
相关系数的计算有两种,一种叫Pearson相关系数(默认);另外一种叫Spearman相关系数(使用非常少)。从理论上讲,数据分布呈现出不正态时则使用Spearman相关系数,但无论是Pearson或者Spearman相关系数,其实际依旧是研究相关关系,结论上并不会有太大区别;并且数据正态分布通常在理想状态下才会成立。因而现实研究中使用Pearson相关系数的情况占绝大多数。
-
-
3、操作
-
本处区分了X和Y,所以对应放入即可。如果并不区分X或者Y,此时直接把所有项放入“分析项Y(定量)”框中即可。
-
-
4、SPSSAU输出结果
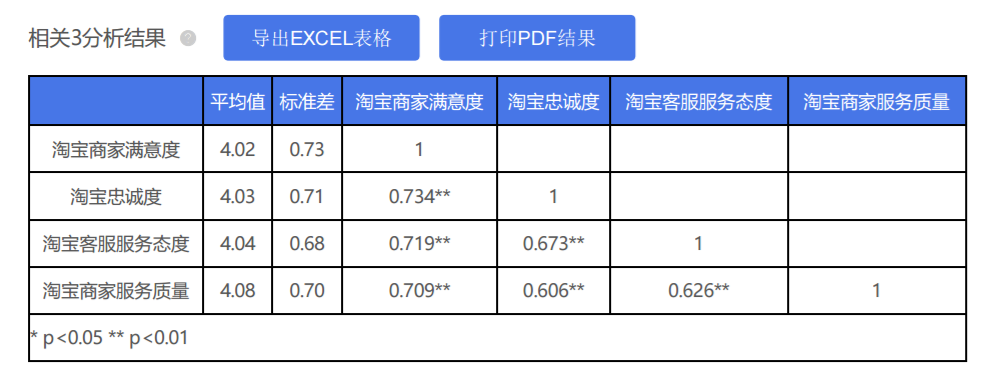
当然也可以输出这样的格式【当所有项均放入同一个框中时】,如下(下表格中还输出平均值和标准差,常见格式,意义不大):
-
5、文字分析
-
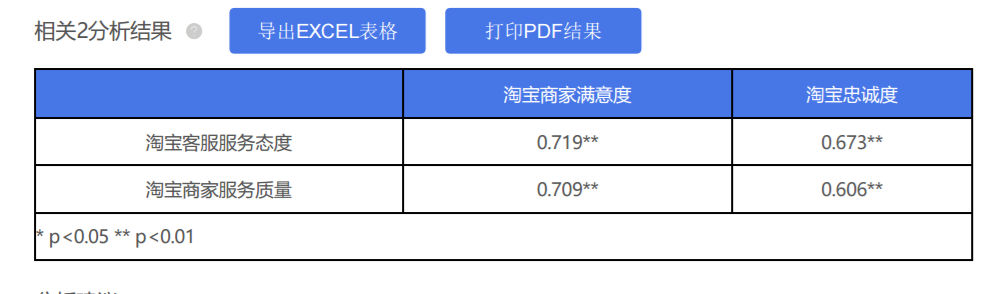
上表使用相关分析去研究“淘宝商家满意度”,“淘宝忠诚度”分别与“淘宝客服服务态度”,“淘宝商家服务质量”之间的相关关系情况,并且使用Pearson相关系数去表示相关关系情况。从上表可以看到:
-
“淘宝商家满意度”分别与“淘宝客服服务态度”,“淘宝商家服务质量”之间均呈现出显著性(p <0.01),并且相关系数值均高于0.7,说明“淘宝商家满意度”分别与“淘宝客服服务态度”,“淘宝商家服务质量”之间均有着非常紧密的正向相关关系。类似的,“淘宝忠诚度”分别与“淘宝客服服务态度”,“淘宝商家服务质量”之间也会有着非常紧密的正相关关系,相关系数值分别是0.673和0.606。
-
-
6、剖析
相关分析仅仅是研究有没有关系与否,如果从常理上应该有关系,那么相关系数总会呈现出显著性。通常来说,相关分析之后还需要接着研究影响关系,使用回归分析方法。:
疑难解惑
-
p 值在哪里呢?
-
p 值(也称显著性值或Sig值),对于相关分析,一般规范的表格格式是:p 值使用*号表示(标识在相关系数的右上角),p < 0.01使用2个*号表示;p < 0.05使用1个*号表示。同时 SPSSAU也提供一个带具体p 值的结果表格。
-
针对问卷量表数据,几个题表示一个维度,如何处理?
-
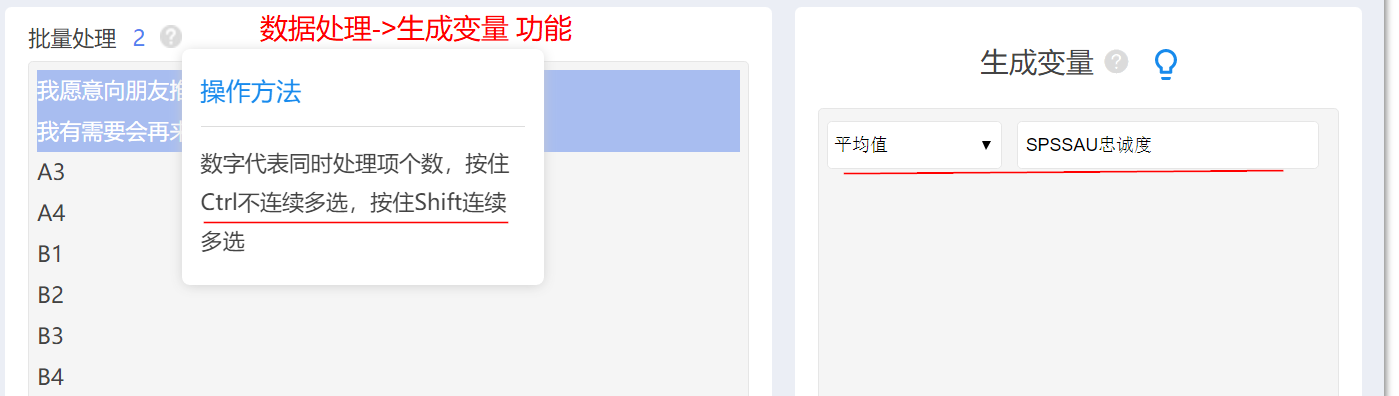
比如有两个题“我愿意向朋友推荐SPSSAU”,“我有需要会再来使用SPSSAU”,此两个题是“忠诚度”的体现。但现在需要“忠诚度”这个整体,而不是具体两个标题,此时如何办呢?
-
相关分析不正态时如何办?
-
理论上讲,如果数据正态分布时,可使用Pearson相关系数进行相关分析;如果数据不正态时,则使用Spearman相关系数进行相关分析。但理论上的正态分布基本没有,只要数据非正态情况在可接受范围内则可继续使用Pearson系数;而且一般情况下Pearson和Spearman系数的结论基本保持一致。所以绝大多数研究均是使用Pearson相关系数,而较少使用Spearman相关系数。
-
多个量表题表示一个维度?
-
比如有两个题“我愿意向朋友推荐SPSSAU”,“我有需要会再来使用SPSSAU”,此两个题是“忠诚度”的体现。可使用SPSSAU【数据处理->生成变量(平均值)】功能完成。通常将多个题概括成一个整体之后,则可以进行相关分析、回归分析、方差分析等(以整体进行,而不需要以题项分别进行)。
-
相关分析里面为Kendall相关系数具体类型是什么?
-
SPSSAU相关分析时,下拉参数中Kendall相关具体为Kendall tub_b。
