结构方程模型不达标调整
-
案例数据下载 下载
-
1、不达标原因
在实际研究中,结构方程模型容易出现不达标现象,比如卡方自由度,RMSEA,CFI值等不达标,至于出现不达标的原因,可能包括几点,分别是‘不正确使用’、‘测量关系不好’、‘模型不好’和‘数据质量差’,如下表格所述:
原因 说明 不正确使用 结构方程模型通常是量表类问卷研究时使用。如果仅研究多个X和多个Y之间的关系,需要使用结构方程模型的特例形式即路径分析。
如果不是问卷量表类数据,比如经济指标数据,研究上也可以使用,有时候也能得到良好的结构,但多数情况下会出现拟合指标不好的现象。测量关系不好 结构方程模型包括测量关系和影响关系两种结构,测量关系不在分析范畴但其会影响模型拟合指标。
比如A维度包括A1~A5共5个指标,但A1这个指标就不能很好的测量A维度。模型不好 模型不好是指影响关系结构不佳,可能是其理论依据不足。
比如想研究A维度影响B维度,但事实上本身就没有影响关系。数据质量差 数据质量差包括‘样本不足’和‘不真实数据’。
通常情况下结构方程模型希望样本量大于200,经验上最好是分析项个数的10倍以上较好。
‘不真实数据’会带来‘测量关系不好’或‘模型不好’。关于‘不正确使用’,准确来讲是在结构方程模型有一定适用性,并非所有测量数据均能很好的使用该模型。比如性别一类的类别数据,其放入结构方程模型中,通常只会得到糟糕的结果。因而研究者需要有提前预知,以免出现数据完成后无法进行分析的尴尬。
关于‘测量关系不好’,此种情况的处理,通常是基于前期的预判和处理。包括前期通常需要进行探索性因子分析,接着使用验证性因子分析,确实测量关系没有问题后再进行结构方程模型,减少‘测量关系不好’对模型带来的干扰。
关于‘模型不好’,其是指模型设置的影响关系与实际数据出现较大偏差,此种情况可结合研究者自身专业知识进行判断,也可结合MI指标进行修正,也或者进行下述的‘模型调整法’处理等。
关于‘数据质量差’,如果样本较少建议加大样本量,如果是‘不真实数据’,那么其会带来‘测量关系不好’,因而会带来一系列连锁问题。
-
2、处理思想
上述中的四大原因时,不正确使用和数据质量差不在考虑范畴。本部分主要是针对‘测量关系不好’和‘模型不好’两种情况,阐述如何进行调整,便于得到科学的模型结果。经验上看,结构方程模型的调整可分为两大方式,分别是‘MI指标调整法’和‘模型调整法’,如下表格说明:
调整方式 说明 MI指标调整法 结合MI指标进行模型调整,具体可再分为两种,分别是:
√ 建立协方差关系
√ 建立影响关系模型调整法 直接针对模型进行调整,具体可再分为以下方式,分别是:
√ 模型拆分法
√ 路径分析法
√ 线性回归法MI指标调整法是指让SPSSAU输出MI修正指标建议值,然后结合该指标进行模型的优化,具体模型优化又包括建立协方差关系和建立影响关系,此种做法的目的在于优化‘测量关系不好’和‘模型不好’。多数情况下结合MI修正指标值是进行协方差关系调整。
MI修正指标表示固定或约束参数时,其可为模型带来的预期卡方减少量,因而从原理上该修正可对卡方自由度这个重要的评价指标带来帮助,理论上对其它指标的帮助通常不会太大,但从经验角度上看,结合MI指标进行模型修正后,通常各项指标均有一定改善,只是相对来看,卡方自由度指标的减少较为明显。
MI指标调整法是对原有模型的‘修缮’,此种处理方式并不会改变模型的核心假设或者结构等,因而在实际研究中使用较为广泛。从科学角度上看,适当的结合MI指标进行模型调整合理,但不能过度依赖于该指标,因为模型带实际专业分析意义,还需要结合自身专业知识进行综合判断处理。
模型调整法是指针对模型进行调整,包括3种方式分别是模型拆分法、路径分析法和线性回归法。模型拆分法是指将复杂的结构方程模型进行分拆,分拆成多个小的结构方程模型,此处理可将模型简化,从而更容易让模型达标,通常情况下越为复杂的模型其要求越高,越简单的模型越易达标。路径分析法是指使用路径分析(path analysis)进行研究影响关系,结构方程模型考虑测量关系和影响关系,而路径分析是结构方程模型的一种特例,其完全不用考虑测量关系,因而此种做法相当于是放弃‘测量关系’,其达到简化模型的作用,最终让模型更易达标。
除此之外,还可考虑使用‘线性回归法’,即放弃结构方程模型,而使用传统的线性回归法,此种做法是改变研究方法,在不得已情况下可以采用。
-
3、SPSSAU操作
上一部分阐述处理思想后,本部分分别从5种调整方式上逐一阐述SPSSAU的设置过程,分别如下5部分。
3.1 建立协方差关系(MI调整法)
结合MI指标建立协方差关系,其共分为2个步骤,首先建立SEM模型时,让SPSSAU输出MI指标,接着结合MI指标建立协方差关系。
第1步:让SPSSAU输出MI指标;
-
MI指标值非常多,因此一般选择比如“MI>10”进行输出,为演示方便,本操作按“MI>3”这个标准输出MI指标值。
-
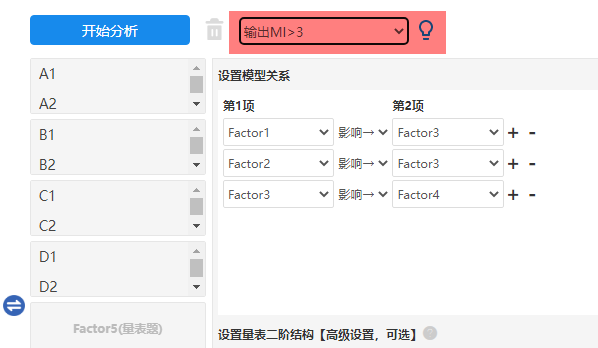
-
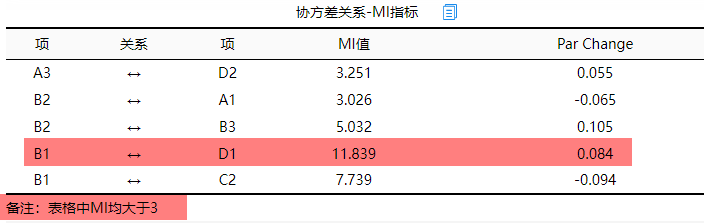
在‘协方差关系-MI指标’表格中,可得到MI修正值结果,如下图:
-
-
从图可以看到,如果B1和D1之间建立协方差关系,意味着预期可以减少卡方值为11.839,因而可考虑建立该两项之间的协方差关系。此处MI值多大算大,其实并没有固定标准,其为一个相对大小标准,经验上如果该指标值大于50时则需要建立。
第2步:建立协方差关系。
-
至于如何在SPSSAU系统中处理,如下图所示,在‘模型关系’处建立B1与D1之间的‘相关关系’。
-
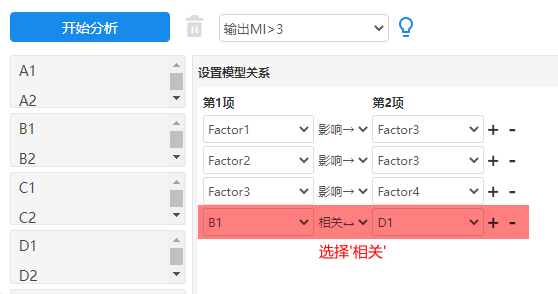
-
其原理如下图,即B1与D1之间建立‘协方差关系’。
-
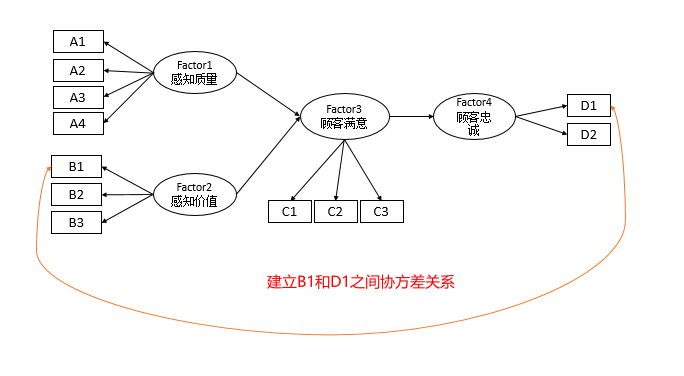
-
协方差关系的调整是一个逐步优化的过程,通常先将MI值非常大的两两项建立关系,然后进行拟合指标查看对比,直至MI值均较小,或者拟合指标基本达标即可。
提示
3.2 建立影响关系(MI调整法)
结合MI指标建立影响关系,其共分为2个步骤,首先建立SEM模型时,让SPSSAU输出MI指标,接着结合MI指标建立影响关系。
第1步:让SPSSAU输出MI指标;
-
MI指标值非常多,因此一般选择比如“MI>10”进行输出,本演示按“MI>3”这个标准进行如下图。
-
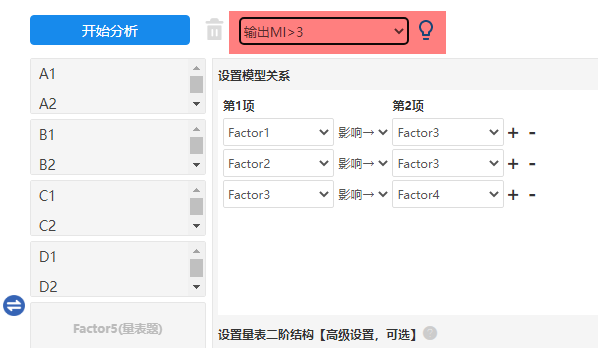
-
在‘影响关系-MI指标’表格中,可得到MI修正值结果,如下图:
-

-
从图可以看到,如果建立Factor对Factor4的影响关系,意味着预期可以减少卡方值为3.076,事实上此值已经较小,经验上可能需要对MI>20或更高的两两项建立关系才可以,除此之外,更为关键的是‘是否要建立影响关系,需要结合专业知识考虑’。
第2步:建立协方差关系。
-
至于如何在SPSSAU系统中处理,如下图所示,在‘模型关系’处建立Factor1对Factor4的影响关系。
-
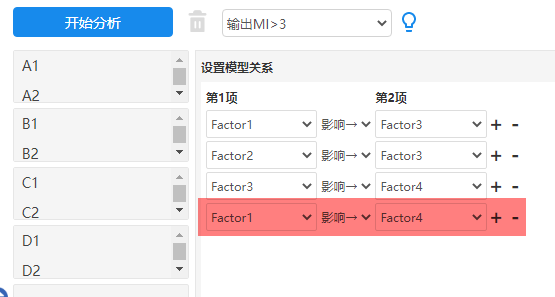
-
其原理如下图,即建立‘Factor1对于Factor4的影响关系’。
-
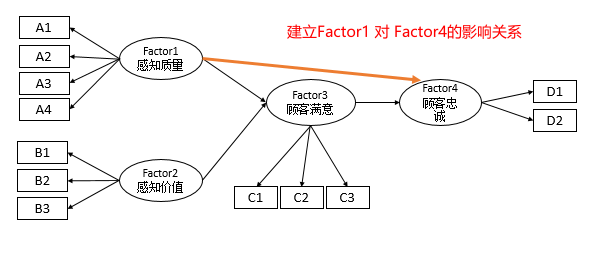
-
影响关系的调整涉及到专业知识,很多时候专业角度不允许建立这样的关系时,此不可进行,以及MI值多大算大时,建立综合对比选择,其并不固定标准,一般建议MI>20时则可考虑建立,直至各拟合指标达标。
提示:
3.3 模型拆分法(模型调整法)
-
模型拆分法是指将模型进行简化,比如将一个模型拆分成2个甚至更多个,类似下图将模型拆分成2个,分别进行研究,从而简化模型。具体思路如下图,操作不再演示。
-
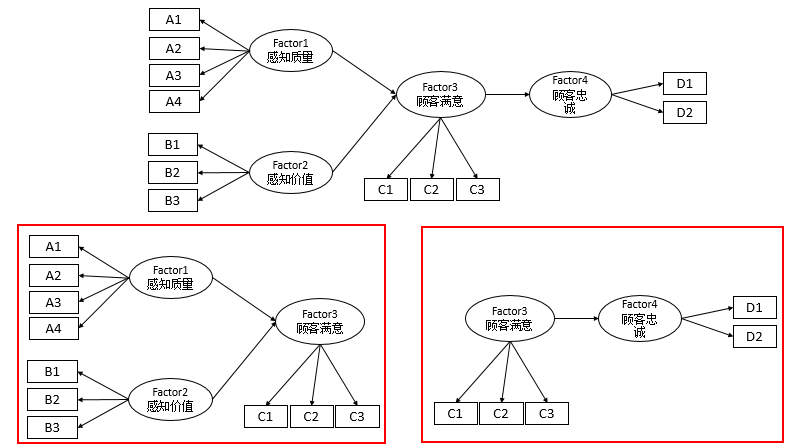
3.4 路径分析法(模型调整法)
-
路径分析法是结构方程模型的一种特例,其完全不考虑‘测量关系’,意味着结构方程模型时少了一种考虑因素,也在简化模型。其处理分为两个步骤,第1步是将潜变量变成显变量,第2步是建立模型。
-
关于‘潜变量变成显变量’,如果是量表类数据,通常是取平均值,比如Factor1由A1~A4共4项表示,因而取该4项平均值,得到显变量,类似其它Factor也是一样的处理,最终利用显变量建立路径分析。关于‘取平均值’这一操作,SPSSAU系统中数据处理-》生成变量功能中有,操作如下图所示:
-
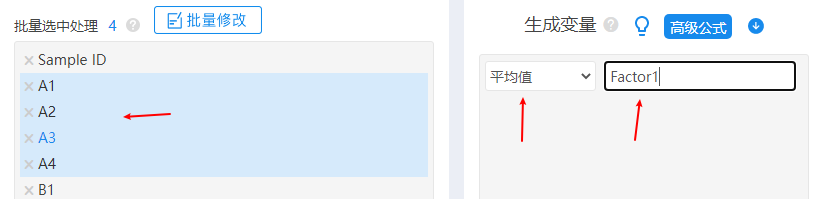
-
接着另外3个Factor也是类似的操作,得到显变量之后,接着进行路径分析,如下图所示:
-

-
建立完成路径分析后,也可结合MI指标进行协方差关系修正或影响关系修正等,此原理或思想与3.1和3.2部分一致。
3.5 线性回归法(模型调整法)
-
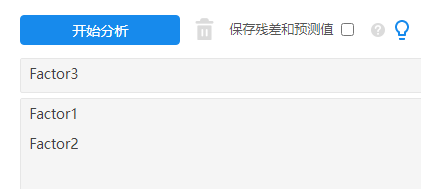
如果路径分析法依旧不达标,意味着同时研究多个X与多个Y之间的影响关系时,模型不适合,因而可将路径分析分别拆分成比如‘1个模型中只有1个Y’,也或者直接使用线性回归重复多次进行分析即可。SPSSAU操作如下图:
-
-
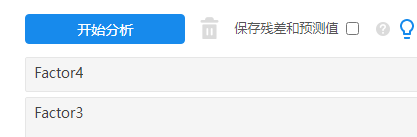
上图展示Factor1和Factor2对于Factor3的线性回归模型构建。下图展示Factor3对Factor4的线性回归模型构建。
-
-