1、背景说明

熵值法（熵权法）是一种研究指标权重的研究方法，比如有5个指标，分别为指标1到指标5，并且有很多样本（比如100个样本），即100行*5列数据，此时研究该5个指标的权重分别是多少。

但从上述可以看到，数据格式上为100个样本即100行数据。如果说当前是面板数据即比如100家公司分别5年，那么就是100*5=500行数据，依旧还是5个指标，即500行*5列数据。此时希望利用熵值法研究该5个指标的权重情况，应该如何处理呢？

2、数据格式

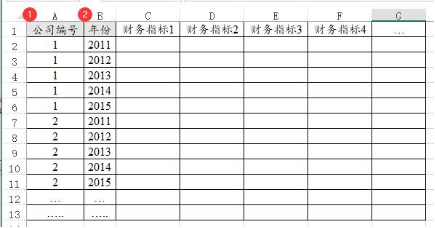
首先从数据格式上，应该类似下图，即有2列数据分别标识公司ID和年份，比如当前为100家公司分别5年，那么就有100*5行的数据。

3、面板数据如何进行熵值法？

熵值法的原理是利用‘熵’来计算权重，‘熵’用来标识信息的不确定性情况，熵越大意味着不确定性越大->信息量越小->权重越小，这是熵值法的原理。

从原理角度上看：

• 面板数据要想计算出5个指标的权重，也是利用‘熵’来计算，也即说明只要能计算出数据的‘熵’值，即可得到权重。而‘熵值’的计算上，并不会考虑是否为面板数据，因而从原理角度，面板数据与普通数据完全一致，直接放入分析即可。

从分析角度上看：

• 针对面板数据，通常有两种做法，分别是做1次，分别重复多次再汇总，如下表格所示：

  分析做法	说明
  一次法	完全不考虑是否面板数据，直接与普通数据一样做一次分析即可
  多次法	比如5年数据，先筛选出第1次的数据做1次，接着重复做另外4次，分别得到5次权重，然后将权重求平均值。

  一次法，此种做法非常常见，即完全不考虑是否为面板数据，在原理上并没有任何问题。因为熵值法计算权重的原理是利用‘熵’值信息，相当于把100家公司5年即500个数字当成一个序列，计算该序列的‘熵’用于判断该500个数字的不确定性情况。最终得到权重。

  另外也可分别筛选出某年数据后，基于100家公司即100个数字看成1个序列，计算该100个数字的不确定性情况，并且最终得到权重，此法称作多次法。

接下来将以案例进行说明：

4、案例说明

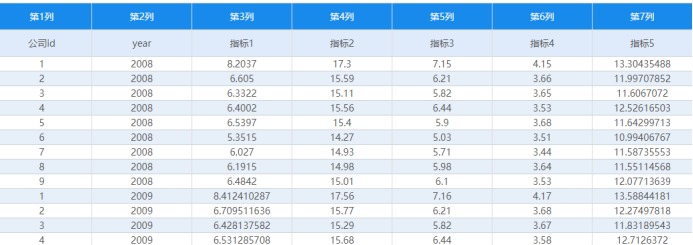
接下来以一份数据，9个公司id，并且5年（2008~2012）的数据进行熵值法。并且分别以整体做1次，和分别5年做5次。数据类似如下：

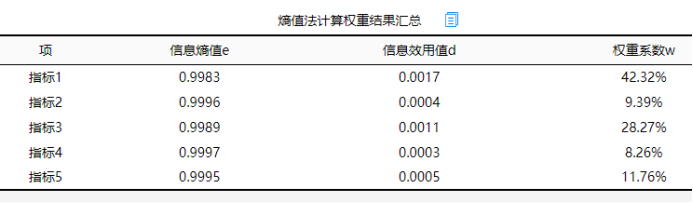
如果仅做1次分析，即将该5个指标直接放入分析框中，结果如下：

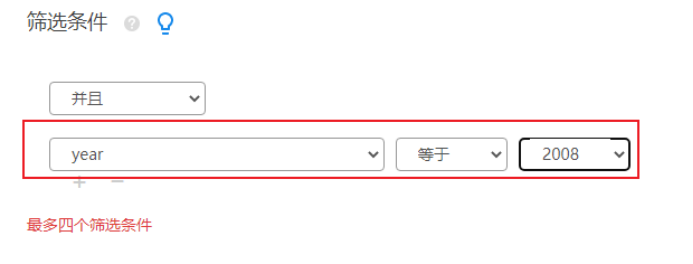
接着分别筛选出2008年的数据做1次分析，并且重复另外4次，关于SPSSAU进行样本筛选，如下截图：

分别进行5次，并且将5次的权重结果进行汇总整理如下表所示：

比如上表格，分别做5次分析，每次均得到5个指标的权重，然后整理后，再对某个指标下的几个权重，比如表格中第2列5个数字求平均得到41.34%，即为最终指标1权重。

特别提示：上述处理从原理上可行，并且此种做法是出于分析考虑，这种做法考虑了不同年份时数字的波动差异性。

5、其它说明

面板数据进行熵值法分析前是否需要进行量纲化处理？如果进行量纲化处理，比如归一化处理，其意味着将数据全部压缩在0~1之间，此时所有指标的数据量纲完全一致，即每个指标数据的信息熵的度量范围也完全一致。如果不进行量纲处理，意味着所有指标的大小有着相对大小意义，从数学原理上不进行量纲处理也可以进行熵值法分析。

是否需要量纲化处理，这本身没有固定要求，通常是结合实际研究意义和文献作为标准，如果有担心，建议进行归一化处理（也或者SPSSAU区间化处理）后再进行分析即可。

另提示：进行某些量纲处理比如归一化处理后会出现数字0，但是熵值时有求log处理，因而数字0会出现无法计算的现象，当然可使用SPSSAU的非负平移功能，选中SPSSAU非负平移，系统会在出现0的指标时，在该指标全部加上一个很小的数字0.001。非负平移也可在分析之前处理好数据再使用均可（SPSSAU数据处理->生成变量->非负平移）。