调节作用SPSSAU深度剖析
一、调节作用原理及剖析
-
调节作用研究指X对于Y的影响时,M的不同时,X对Y的影响幅度是否不一致。使用SPSSAU进行调节作用时,可通过两个方法功能进行实现,分别是问卷研究模块里面的调节作用方法,也或者进行方法模块里面的分层回归方法。
-
在进行调节作用研究时,共涉及两大块理论内容。分别是X和M的数据类型识别和数据处理两个角度阐述,且数据处理分析定类数据哑变量处理和定量数据中心化处理。
-
如果X或M为潜变量并且希望使用结构方程模型进行调节作用研究,可查阅SPSSAU帮助手册的单独文档剖析。
1.X和M数据类型
| 编号 | X自变量 | M调节变量 | SPSSAU首选方法 | SPSSAU备选方法 |
| 1 | 定量 | 定量 | SPSSAU->问卷研究->调节作用 | SPSSAU进阶方法->分层回归 |
| 2 | 定量 | 定类 | SPSSAU->问卷研究->调节作用 | SPSSAU进阶方法->分层回归 |
| 3 | 定类 | 定量 | SPSSAU->问卷研究->调节作用 | SPSSAU进阶方法->分层回归 |
| 4 | 定类 | 定类 | SPSSAU->进阶方法->双因素方差 |
-
第一种情况:X为定量,M为定量;此时可使用SPSSAU问卷的调节作用模块,设置好数据类型即可进行分析。如果X或者M的个数为多个,此时使用SPSSAU进阶方法的分层回归。
-
第二种情况:X为定量,M为定类;此时可使用SPSSAU问卷的调节作用模块,设置好数据类型即可进行分析。如果X或者M的个数为多个,此时使用SPSSAU进阶方法的分层回归。
-
第三种情况:X为定类,M为定量;此时可使用SPSSAU问卷的调节作用模块,设置好数据类型即可进行分析。如果X或者M的个数为多个,此时使用SPSSAU进阶方法的分层回归。
-
第四种情况:X为定类,M为定类;此时可使用SPSSAU进阶方法的双因素方差。
-
SPSSAU问卷研究模块中的调节作用方法,其仅支持放入1个X和1个M,如果有多个X或者多个M,此时需要使用SPSSAU进阶方法中的分层回归。当然也可重复进行多次分析,然后汇总表格结果。
-
针对X或者M在不同的数据类型进行调节作用,统一的处理原则为‘定类作哑变量处理,定量作中心化处理’。具体接下来说明:
2.数据处理之哑变量处理
关于直接使用SPSSAU问卷研究模块里面的调节作用方法,可直接设定某项数据为定类数据,此时SPSSAU系统默认则会进行哑变量设置。如下图:
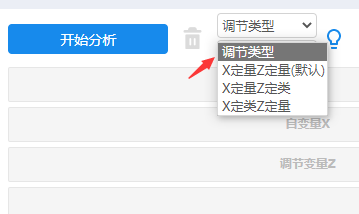
但是SPSSAU问卷研究模块中的调节作用分析方法,仅支持X和M均为1项时,如果超过1项时,此时研究人员也可使用SPSSAU数据处理->生成变量功能里面的哑变量,然后设置好哑变量之后,再使用SPSSAU进阶方法里面的分层回归进行分析。如下图:
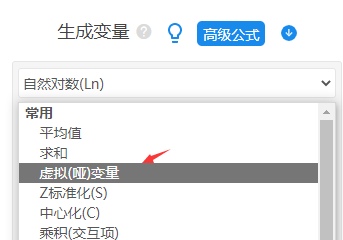
3.数据处理之中心化处理
针对X或者M,原则统一为‘定类数据哑变量,定量数据中心化’。
如果X,也或者M为定量数据,通常情况下需要进行量纲处理,一般是使用中心化处理。如果是使用SPSSAU问卷研究模块里面的调节作用,默认为中心化处理(也可下拉参数设置,让系统不进行处理,或者进行标准化处理)。如下图:
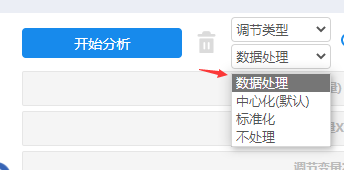
如果使用SPSSAU进阶方法里面的分层回归,此时需要自行对定量的X或者M进行中心化(或标准化处理),可使用数据处理里面的生成变量功能。
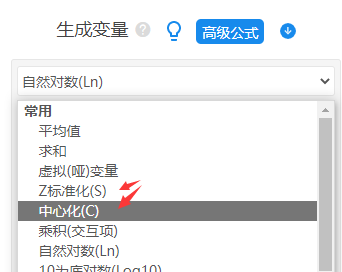
二、调节作用分析流程
如果X和M均为1项,此时建议直接使用SPSSAU->问卷研究模块->调节作用即可进行分析(如果X和M均1项且均为定类,则使用双因素方差)。如果X或M超过1项时,此时本部分分析结合上述四种情况讲解如何使用分层回归进行研究。下述中以X为2个,M为1个为例(不包括第4种情况即X和M均为定类这一特殊情况),实际研究中,X为多个或M为多个时,均类似的处理方式即可。
| 编号 | X自变量 | M调节变量 | 备注说明 | SPSSAU研究方法 |
| 1 | 定量 | 定量 | X为2个,M为1个 | SPSSAU进阶方法->分层回归 |
| 2 | 定量 | 定量 | X为2个,M为1个 | SPSSAU进阶方法->分层回归 |
| 3 | 定量 | 定量 | X为2个,M为1个 | SPSSAU进阶方法->分层回归 |
| 4 | 定量 | 定量 | X为1个,M为1个 | SPSSAU进阶方法->双因素方差 |
2.1 X定量为2个, M定量为1个

-
首先分别针对定量数据的2个X和1个M进行中心化,然后将中心化后的数据分别得到交互项(即相乘乘积项),总共2个,然后进行分层回归。
-
分层回归时,原理上第1层放入自变量X(处理后),第2层放入M(处理后),第3层放入交互项。
-
如果说交互项呈现出显著性,则说明具有调节作用,如果交互项回归系数显著且大于0则说明正向调节,反之则说明负向调节。
2.2 X定量为2个, M定类为1个

-
首先针对定量数据的2个X进行中心化,并且针对定类的M进行哑变量设置,并且参照项为dummyM_0,接着进行交互项生成。最后进行分层回归。
-
分层回归时,原理上第1层放入自变量X(处理后),第2层放入M(处理后),第3层放入交互项。
-
如果说交互项呈现出显著性,则说明具有调节作用,如果交互项回归系数显著且大于0则说明正向调节,反之则说明负向调节。
2.3 X定类为2个, M定量为1个

-
首先分别针对定量数据的X和M进行中心化,然后将中心化后的数据分别得到交互项(即相乘乘积项),然后进行分层回归。
-
如果说交互项呈现出显著性,则说明具有调节作用,如果交互项回归系数显著且大于0则说明正向调节,反之则说明负向调节。
2.4 X定类为1个, M定类为1个
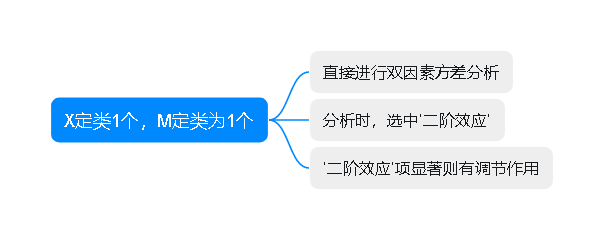
三、SPSSAU操作说明
本部分分别阐述如何利用SPSSAU进行操作说明,并且结合X和M的数据类型进行分别阐述。
3.1 X定量为2个, M定量为1个
针对X和M均为定量数据时,首先将2个X和1个M均进行中心化处理。如下图:
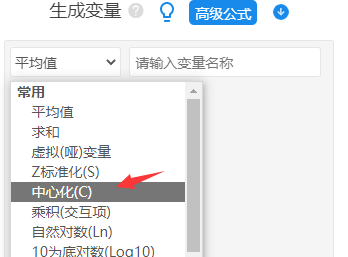
处理之后,得到X1与M的交互项,X2与M的交互项【重复操作2次即可】。如下图操作:
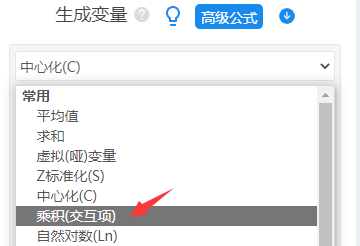
在完成数据处理之后,接着进行分层回归分析,操作如下图:
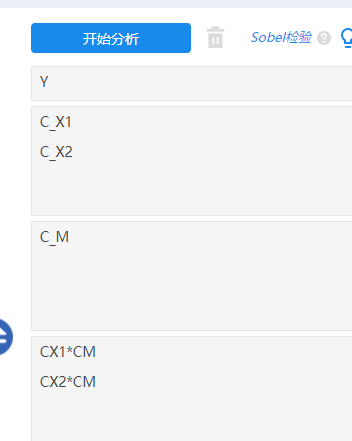
最后关于调节作用的分析上,只需要针对SPSSAU输出表格结果中交互项的回归系数显著性情况进行分析即可(共2个交互项),如果交互项呈现出显著性,那么就说明具有调节作用。如果呈现出显著性,则交互项的回归系数大于0则说明具有正向调节作用,反之交互项呈现出显著性且回归系数小于0则说明具有负向调节作用。
3.2 X定量为2个, M定类为1个
针对X为定量,M为定类,此时首先针对定量的2个X进行中心化处理,并且针对定类M进行哑变量处理。如下图:
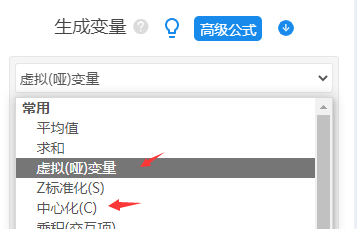
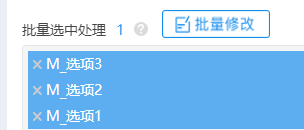
处理之后,接着进行交互项设置,M是定类数据(且有3个选项),此时哑变量设置后会得到3个标题(分别是M_选项1,M_选项2,M_选项3),M_选项1作为参照项,因此不进行交互项设置。2个中心化后的X,以及哑变量留下一个参照项后余2项(分别是M_选项2,M_选项3),因而最终为2*2=4个交互项,重复进行4次交互项设置即可,如下图操作:
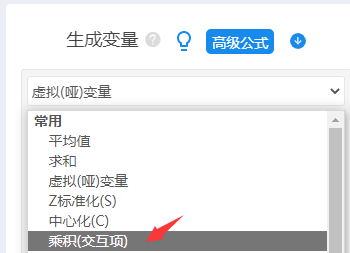
在完成数据处理之后,接着进行分层回归分析,第1层放入中心化后的X,第2层放入哑变量设置后的2个哑变量项(其中有1项作为参照项不放入),第3层放入4个交互项,操作如下图:
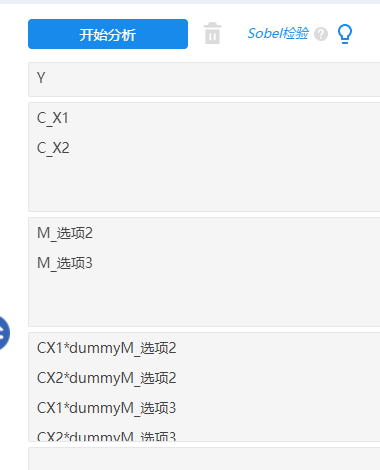
最后关于调节作用的分析上,只需要针对SPSSAU输出表格结果中交互项的回归系数显著性情况进行分析即可(共计4个交互项),如果交互项呈现出显著性,那么就说明具有调节作用。如果呈现出显著性,则交互项的回归系数大于0则说明具有正向调节作用,反之交互项呈现出显著性且回归系数小于0则说明具有负向调节作用。
3.3 X定类为2个, M定量为1个
-
如果X为2个且均为定类数据,那么分别针对2个X进行哑变量设置,得到哑变量后,将其与定量的M(且中心化处理后),进行交互项生成。本部分假定X1的类别数量为3,X2的类别选项数量也为3,因此X1得到3个哑变量,X2得到3个哑变量,X1和X2分别均需要留下一个参照项,那么X1余2个哑变量与中心化后的M进行交互项生成,X2余2个哑变量与中心化后的M进行交互项生成。总共得到2+2共计4个交互项。
-
关于X1和X2进行哑变量生成,且M进行中心化处理,且X1的2个哑变量和X2的2个哑变量分别与中心化后的M进行交互项生成,操作如下:
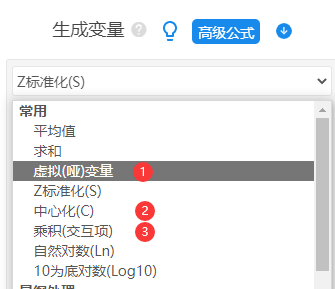
将X1和X2均进行哑变量设置后,接着进行分层回归分析。第1层放入X1的2个哑变量和X2的2个哑变量,第2层放入中心化后的M,第3层放入2+2共计4个交互项。操作如下图:

最后关于调节作用的分析上,只需要针对SPSSAU输出表格结果中交互项的回归系数显著性情况进行分析即可(共计4个交互项),如果交互项呈现出显著性,那么就说明具有调节作用。如果呈现出显著性,则交互项的回归系数大于0则说明具有正向调节作用,反之交互项呈现出显著性且回归系数小于0则说明具有负向调节作用。
3.4 X定类为1个, M定类为1个
如果X和M均为1个,且均为定类数据(只能X和M均为定类数据,且个数一定为1个),此时可使用SPSSAU进阶方法里面的双因素方差分析进行研究(不需要进行哑变量设置等),并且选中‘二阶效应’(即交互项),操作如下图:
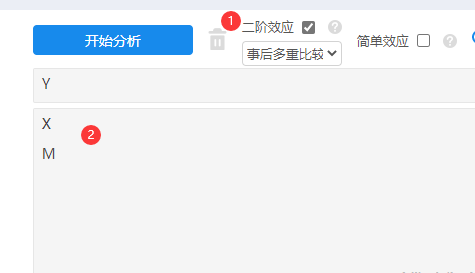
最后关于调节作用的分析上,只需要针对SPSSAU输出表格结果中交互项的显著性情况进行分析即可(只有1个交互项),如果交互项呈现出显著性,那么就说明具有调节作用。至于调节作用的进一步分析,则可使用SPSSAU默认生成的交互图等综合进行研究剖析即可。
四、总结
-
综上所述:除X和M均为1个使用双因素方差分析这种特殊情况外。其余的情况下,只要X或M是定类数据,那么就进行哑变量设置,只要X或M是定量数据则需要进行中心化处理。哑变量或中心化处理之后,接着进行交互项生成。哑变量处理后,一定记得参照项(一般是第1项)不进行交互项生成,也不会放入分层回归中。
-
分层回归进行调节作用分析时,一般第1层放入X(哑变量或中心化处理之后的),第2层放入M(哑变量或中心化处理之后的),第3层放入所有的交互项。
-
至于调节作用的检验上,通常情况下是针对交互项的显著性进行剖析即可,如果交互项显著,则说明具有调节作用,进一步的调节作用分析等,则需要结合交互项的回归系数方向(或自行绘制图形等)进行研究。
-
调节作用的原理是数据处理(包括哑变量或中心化,交互项)之后进行分层回归,此操作过程步骤较多,如果X和M个数均为1个,建议使用SPSSAU问卷研究模块里面的调节作用分析方法即可。如果X或M的个数超过1个,建议可重复性地使用SPSSAU问卷研究模块里面的调节作用分析方法即可。SPSSAU问卷研究模块里面的调节作用分析方法,其内部原理即为分层回归(且会自动进行数据处理等),方便易用,研究人员需要理解核心的内部原理后,方能游刃有余地使用SPSSAU完成科学研究。
-
除此之外,如果X或M为潜变量并且希望使用结构方程模型进行调节作用研究,其核心原理基本一致,也是数据处理,交互项生成,然后放入模型分析等,但内部的细节处理等差异很大,可查阅SPSSAU帮助手册的单独文档剖析。