Turf组合模型
-
案例数据下载 下载
Turf(Total Unduplicated Reach and Frequency),累计不重复到达率和频率分析模型。比如手机厂商有10种手机颜色备选方案,但手机厂商觉得颜色太多成本过高,消费者也有选择困难。因此需要从10种颜色中找出其中3种(或者2种/4种/5种等均可),以最小的组合覆盖最多的群体。此时可做个调研,然后得出科学决策,此则为Turf模型解决的问题。最初其应用于广告传媒领域,现在较广泛地用在新产品开发(比如餐厅设计菜品、汽车配置组合等),也有的用于投资策略组合等。
问卷设计上,比如有10种颜色,其设计为一个多选题共有10个选项代表10种颜色,每个选项只有两个答案,分别是喜欢不喜欢啥,选中喜欢则为数字1,不喜欢则为0(此为多选题默认的计分方式),最终得到10列数据。那么最终应该推出哪3种颜色呢?
思路上,最简单的方式直接是排名前三的颜色即可,但这种思路有个问题,汽车厂商并不是提供最喜欢的前三种,而是希望推出的颜色可以覆盖各类人群,那么此时哪三种颜色组合在一起,可以覆盖到最多的人群,即是Turf组合模型解决的问题。
Turf组合模型案例
-
1、背景
某企业正研发一款儿童手机,出于时间压力和用户偏好考虑,现仅希望推出3种颜色的配置,希望该3种颜色可以最大化覆盖群体偏好,因而首先进行一项调研分析,设计一项多选项,该多选题共有10个选项,每个选项的问题为:“你对**颜色喜欢吗?”,答案仅为两项分别是喜欢和不喜欢,最终收集到共计99个儿童调研问卷。最终整理好的数据类似如下图所示:

上图中的数字1表示喜欢,数字0表示不喜欢,SPSSAU系统中,默认是基于数字1进行计算,即数字1表示选中该项的意思,比如用户1选择颜色 1/2/4/5/9,其意味着用户1对于该5个颜色都有着喜欢偏好。
-
2、理论
Turf组合模型的计算原理较为简单,比如本文档案例只希望选择3个颜色,那么遍历任意3个颜色组合,找出不同组合下的覆盖,然后计算覆盖情况,覆盖率越高那么就选择该组合即可。
-
Turf组合模型涉及一些专业名词如下述:
-
组合:比如黄色和绿色一起就是一种组合,(假定手机厂商要推出3种颜色的手机,3种颜色分别是黄绿蓝,那么这就是一种组合,3种颜色时其组合数量为3);
-
组合数量:比如颜色1和颜色2则组合数量为2;
-
组合个数:比如10种颜色中选择2个颜色,那么数学上的组合个数=C(10,2)=10*9/2=45;
-
触达率(覆盖率、到达率、响应率),比如组合是黄绿蓝,张三喜欢黄色和绿色,张三选中了黄绿蓝这个组合中的黄色,张三就被触达了,触达率 = 触达数 / 总样本量(触达数为被触达的样本数);
-
频数:就是某组合下颜色被选中的次数(比如组合为黄绿蓝,那么黄绿蓝被选中了多少次),频率= 频数 / 总触达次数(总触达次数为10种颜色被所有样本选中了多少次)。
-
需要提示的是:上述中触达率是指某组合前提时,有多少样本被覆盖,该指标为核心指标,频率是基于组合对应项被选中的次数占比。触达率越高意味着覆盖越广泛,频率越高意味着越被更多人喜欢。二者的关注点并不完全一样,Turf模型更多关注于触达率即覆盖广泛度,但常规的分析上一般关注频率较多(即哪些更被喜欢)。
-
-
3、操作
本例子操作如下图:
直接将10个颜色选项放入分析框即可,与此同时,如果明确组合数量只为3即只希望有3种颜色并且覆盖更多群体,那么可选择3个即可。默认情况下是SPSSAU自动寻优,即自动找出可以覆盖最多群体的组合,至于组合数量是多少这个由数据决定。此处自动寻优的数学原理如下所述:
SPSSAU会首先基于组合数量为1即1个颜色时,找出最大触达率对应的1个颜色组合,接着基于该颜色基础上寻找组合数量为2即2个颜色时,找出最大触达率对应的2个颜色组合,依次循环下去直到结束。结束的终点即为组合数量为10,即全部颜色均推出。自动寻优可得到不同组合数量时的最优组合,便于研究者直接使用,并且可通过图示化直观查看不同组合数量下触达率或者频率的变化情况,可基于该结果选择最优组合数量(如果不确定是否3个颜色OK的话)。需要注意的是,自动寻优这一算法求解结果为相对(局部)最优解,并非绝对最优解,研究者可结合自动寻优解结果,以及确定性的组合数量结果时的结果进行对比选择使用。
-
4、SPSSAU输出结果
如果是自动寻优组合数量,那么SPSSAU共输出1个表格和1个图。表格展示不同组合数量时对应的各指标信息值,并且绘图展示不同组合数量时对应的触达率或频率,便于辅助研究者进行判断最优组合数量。如果是有着明确的组合数量(比如本案例明确为3),那么则输出该组合数量时,对应的各种组合及其对应的指标数据。
-
5、文字分析
本次案例结果首先输出自动寻优组合数量的结果如下:
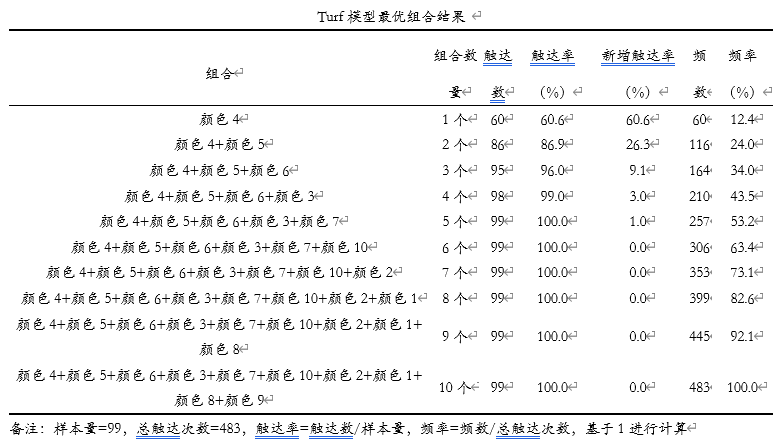
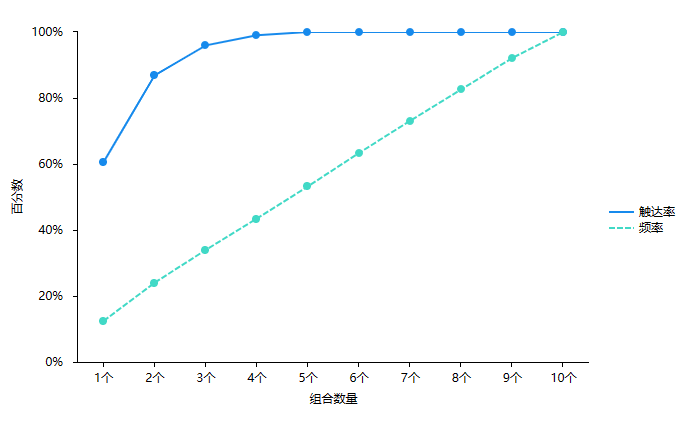
从上表格和下图可以看到,如果组合数量为1,那么‘颜色4’最优,其触达率为60.6%,即该1个颜色就可以覆盖60.6%的样本群体,如果组合数量为2即‘颜色4+颜色5’,此时覆盖度可达86.9%,如果希望3个颜色即‘颜色4+颜色5+颜色6’ 覆盖率可达96%。另外可从下图也可以直观地看到,组合数量为4及更高后,覆盖率不会再变化,即如果仅考虑覆盖广泛度问题,3个颜色就好了。如果考虑的是样本的偏好问题,那么肯定颜色越多越更受喜欢,因为组合数字为1时仅12.4%的喜欢度,即还有87.6%的情况下对其它颜色也喜欢。
与此同时,本案例时已经确定组合数量为3即3个颜色,那么也可设置组合数量为3的结果,如下表格所示:
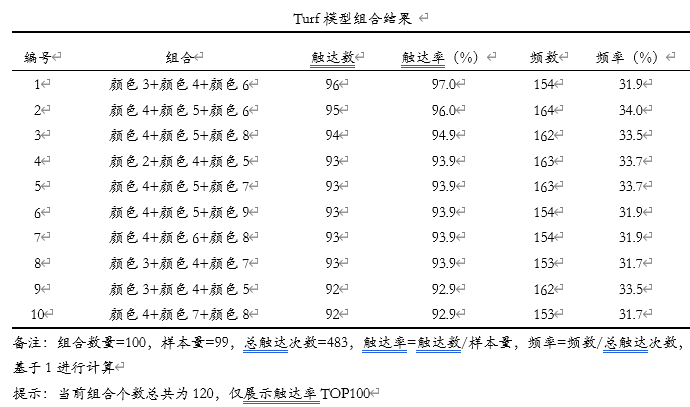
如果组合数量为3,那么会有C(10,3)=120个组合备选,SPSSAU只会输出前100个组合结果,基于篇幅考虑,上表格仅展示前10个组合结果。从上表格可以看到:组合数量为3时,‘颜色3+颜色4+颜色6’是最优组合,其覆盖率为97%,即该3个颜色可以覆盖到97%的群体了,但频率为31.9%,即还有68.1%的情况下会喜欢另外7种颜色。与此同时需要提示的是,上述得到的最优解为‘颜色3+颜色4+颜色6’,但是自动寻优时为‘颜色4+颜色5+颜色6’,二者并不等同,这是由于自动寻优为‘局部最优解’,但主动设置组合数量得到的是‘绝对最优解’所致。
最终手机厂商可考虑只生产3种颜色,因为3种颜色已经可以触达绝大多数群体,生产更多颜色也对覆盖率没有明显的帮助。
-
6、剖析
-
涉及以下几个关键点,分别如下:
-
Turf组合模型时,自动寻优得到的结果是基于‘局部最优解’,而主动设置组合数量的第1个组合为‘绝对最优解’,因而二者很可能不同。
-
数据计算上,SPSSAU默认以数字1进行计算,即需要整理好的数据时数字1表示选择/喜欢/偏好某项。
-
疑难解惑
-
SPSSAU Turf组合模型时仅输出前100个组合?
-
比如有20个分析标题,而且设置组合数量为6,那么计算上应该有C(20,6)=38760个不同的组合,SPSSAU只会输出该38760中触达率TOP100的组合。