折半信度分析

信度分析在于研究数据的可靠真实性，通俗理解即为研究数据是否真实作答。正常情况下，信度分析只会针对量表态度题。

信度的测量上有很多种方法，常见是α系数方法，也称一致性内部信度。除此之外，还有重测信度，折半信度等。重测信度是指同一批样本，在不同时间点做了两次相同的问题，然后计算两次回答的相关系数，通过相关系数去研究一致性水平。折半信度是指将所有量表题项分为两半，计算两部分各自的信度以及相关系数，进而估计整个量表的信度。通常心理学、教育学类经典量表常使用此类方法进行信度质量衡量。其判断标准可参考α信度系数的衡量标准。

折半信度案例

• 1、背景

  有一个满意度量表，由9个量表题进行测量，现希望进行折半信度分析。

• 2、理论

  折半信度是指将所有量表题项分为两半，计算两部分各自的信度以及相关系数，进而估计整个量表的信度。如果说测量题数量为偶数，则刚好两部分题项数量相等，反之则不相等。分析时需要结合两部分题项是否相等，查看对应的折半系数（Spearman-Brown系数）。

  通常心理学、教育学类经典量表常使用折半系数对信度质量衡量。其判断标准可参考α信度系数的衡量标准。如果折半系数值介于0.7~0.8之间；则说明信度较好;如果折半系数值介于0.6~0.7；则说明信度可接受;如果折半系数值小于0.6；说明信度不佳；

• 3、操作

  本例子操作截图如下，在SPSSAU选择信度分析时，右侧下拉框处选择‘折半系数’即可：

  

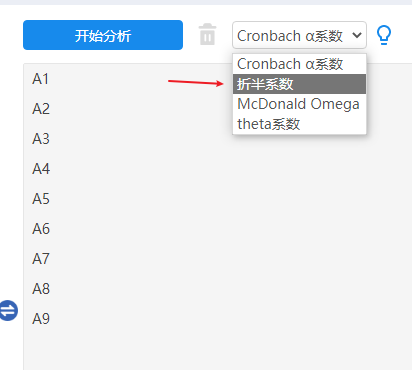
• 4、SPSSAU输出结果

  SPSSAU共输出一个表格，如下：

  折半信度分析
  性别	前半部分	值	0.861
  		项数	5
  	后半部分	值	0.845
  		项数	4
  	总项数		9
  前半部分和后半部分间的相关系数值			0.785
  折半系数（Spearman-Brown系数）	等长		0.880
  	不等长		0.881
  Guttman Split-Half 系数			0.876

  从上表可知：针对满意度涉及的九个量表题项进行分析，折半分成两部分时，两部分分别的分析项数量并不相等，因而应该使用不等长折半系数(Spearman-Brown系数）进行信度质量判断，即最终折半系数值为0.881，大于0.8，因而说明研究数据信度质量高。

  • 特别提示

  • 折半信度会同时输出Cronbach α系数，可以简要描述即可。更多关注于折半系数，有时候还可以直接使用Guttman Split-Half 系数衡量信度质量，但此类情况较少。

• 5、文字分析

  如上一部分

• 6、剖析

  涉及以下关键点，分别如下：

  • 需要结合两部分是否项数是否相等，选择最终的折半系数，即Spearman-Brown系数。

  • 如果仅两个项进行分析，两部分分别均为1项，此时输出Cronbach α系数值为1，并且等长或不等长对应的折半系数完全相同。

  • 信度分析计算公式深入剖析？

  • 具体涉及信度分析的深入分析和公式解读等，可点击查看。