验证性因子分析(confirmatory factor analysis, CFA)是用于测量因子与测量项(量表题项)之间的对应关系是否与研究者预测保持一致的一种研究方法。与验证性因子分析CFA相对应的为探索性因子分析,二者的区别在于,验证性因子分析(CFA)用于验证对应关系,探索性因子分析(EFA)用于探索因子与测量项(量表题项)之间的对应关系。如果是成熟的量表,研究者可同时使用验证性因子分析CFA,和探索性因子分析(简称因子分析,EFA)用于验证量表的效度。如果量表的权威性较弱,通常使用探索性因子分析(EFA)进行探索因子,或者效度检验分析。
验证性因子分析CFA的主要目的在于进行效度验证,同时还可以进行共同方法偏差CMV的分析。效度有很多种,比如内容效度,结构效度,聚合(收敛)效度,区分效度等。各个名称的区别说明如下:
| 项 | 概述 | 使用方法 |
| 内容效度 | 用文字描述量表的有效性,比如具有参考文献来源,量表经过专家认可等 | 文字描述 |
| 结构效度 | 因子与测量项(量表题项)对应关系是否符合预期,如果符合预期则说明具有结构效度 | 探索性因子分析(EFA)和验证性因子分析(CFA)等 |
| 聚合(收敛)效度 | 强调本应该在同一因子下面的测量项,确实在同一因子下面 | 验证性因子分析(CFA)的AVE和CR指标等 |
| 区分效度 | 强调本不应该在同一因子的测量项,确实不在同一因子下面 | 区分效度共3种方式。 第1种是:AVE和相关分析结果对比; 第2种是HTMT法;第3种是MSV和ASV法。 |
如果并非经典量表,通常情况下研究人员会使用探索性因子分析(EFA)进行效度验证,该验证方法一般称作结构效度分析,同时还会使用内容效度进行分析即用文字描述量表的来源设计过程等,用于论证研究量表的有效性。当然如果还想进一步深入分析,亦可使用CFA进行深入研究。
如果是经典量表需要进行效度验证,其内容效度确认无疑,而且使用探索性因子分析(EFA)进行分析时,也具有良好的结构效度。所以研究人员更偏好于使用CFA进行深入分析,即进行聚合(收敛)效度和区分效度分析。
结合实际应用情况,验证性因子分析通常有三个用途。如下表所示:
| 项 | 验证方法 | 其它说明 |
| 聚合(收敛)效度 | AVE(平均提取方差值)和CR(组合信度),因子载荷系数(factor loading) | 一般查看AVE值,也或者查看factor loading值 |
| 区分效度 | AVE平方根值与相关系数比较法, HTMT值法, MSV和ASV指标法 | AVE平方根值与相关系数比较法较为常用 |
| 共同方法偏差(也称同源方法,CMV) | 所有量表项全部放在一个因子里面进行分析 | 需要结合模型拟合指标等综合判断 |
如果目的在于进行聚合(收敛)效度分析,则可使用AVE和CR这两个指标进行分析,如果每个因子的AVE值大于0.5,并且CR值大于0.7,则说明具有良好的聚合效度,同时一般还要求每个测量项对应的因子载荷系数(factor loading)值大于0.7。有时候还可能会结合模型拟合指标,以及进行模型MI值修正,以达到更好的结论。
如果目的在于进行区分效度分析,多数情况下使用‘AVE平方根值与相关系数比较法’,如果每个因子的AVE根号值均大于“该因子与其它因子的相关系数最大值”,此时则具有良好的区分效度,为更好表述,使用下图展示:
| 区分效度:Pearson相关与AVE根值 | ||||
| 因子1(A1~A5) | 因子2(B1~B5) | 因子3(C1~C4) | 因子4(D1~D6) | |
| 因子1(A1~A5) | 0.8426 | |||
| 因子2(B1~B5) | 0.700** | 0.8396 | ||
| 因子3(C1~C4) | 0.646** | 0.720** | 0.9370 | |
| 因子4(D1~D6) | 0.777** | 0.753** | 0.750** | 0.9203 |
| *p <0.05 ** p <0.01 斜对角线数字为该因子AVE的根号值 | ||||
上图的斜对角线为AVE的根号值,比如因子对应的AVE根号值为0.843,该值大于因子1与另外3个因子的相关系数(分别是0.700,0.646和0.777),类似因子2,因子3,因子4也这样进行分析。最终发现因子的AVE根号值,全部均大于该因子与其它因子的相关系数值,因而说明具有很好的区分效度。
除此之外,SPSSAU还提供另外两种区分效度验证方式,分别是HTMT法和MSV/ASV指标法,研究者可结合情况选择使用其中1种或多种即可。
如果目的在于进行共同方法偏差(CMV)分析,常见的做法为:将所有的测量项(即所有因子对应的测量量表题项)放在一个因子里面,然后进行分析,如果测量出来显示模型的拟合指标,比如卡方自由度比,RMSEA,RMR,CFI等无法达标,则说明模型拟合不佳,即说明所有的测量项并不应该同属于一个因子(放在一起时模型不好),因而说明数据通过共同方法偏差CMV检验,数据无共同方法偏差问题。
针对CMV检验,上种思路同样也适用于使用探索性因子分析EFA方法进行检验CMV问题(也称作Harman单因子检验方法),即查看把所有量表项进行探索性因子分析EFA时,如果只得出一个因子或者第一个因子的解释力(方差解释率)特别大,通常以50%为界,此时可判定存在同源方差(共同方法偏差),反之则说明没有共同方法偏差问题。
针对共同方法偏差(CMV)分析,还有其它的一些做法,建议用户以文献为准。
-
特别提示:
-
如果使用CFA进行聚合(收敛)效度,或区分效度分析,建议首先进行探索性因子分析(EFA),然后再进行CFA分析;原因在于CFA对于数据质量要求高,如果探索性因子分析就发现因子与测量项对应关系出现偏差,需要首先进行处理,确认好因子与测量项对应关系后,再进行CFA分析;
-
如果使用CFA进行分析,建议样本量至少为测量项(量表题)的5倍以上,最好10倍以上,且一般情况下至少需要200个样本。
-
一个因子对应的测量项最好在5~8个之间,便于后续删除掉不合理测量项。
验证性因子分析(CFA)案例
-
1、背景
当前有一份215份的研究量表数据,其共由四个因子表示,第一个因子共5项,分别是A1~A5;第二项因子共5项,分别是B1~B5;第三个因子共4项,分别是C1~C4;第4个因子共6项,分别是D1~D6。现希望验证此量表的聚合效度和区分效度,并且希望进行共同方法偏差分析CMV。
-
2、理论
验证性因子分析的步骤大致可分为四步,分别是:模型构建、删除不合理测量项、模型MI指标修正和模型分析
-
第一步:模型构建,即将因子与测量项对应关系放置规范;以及SPSSAU建议研究人员在进行CFA分析前需要进行EFA,首先清理掉对应关系出现严重偏差的测量项;
-
第二步:删除不合理测量项;如果因子与测量项间的对应关系出现严重偏差,此时可考虑删除某测量项;也或者某测量项与因子间的载荷系数值过低(比如小于0.5),说明该测量项与因子间关系较弱,需要删除掉该测量项;
-
第三步:模型MI指标修正;如果说模型拟合指标不佳,可考虑进行模型MI指标修正MI值表示两项间的关联强度,MI值越大说明两项间的关联性越强,如果两项之间的关联性过强会干扰模型,因此需要建立关联关系。此步骤共分为2步,第1步选择参数让SPSSAU输出MI指标值(默认是不输出,以及如果要全部输出,此时MI指标值输出会非常多,因而一般选择输出大于‘某个值’比如‘大于10’的MI指标进行输出。第2步是结合输出结果,建立‘测量项协方差关系’。
-
第四步:最终模型分析。
-
-
3、操作
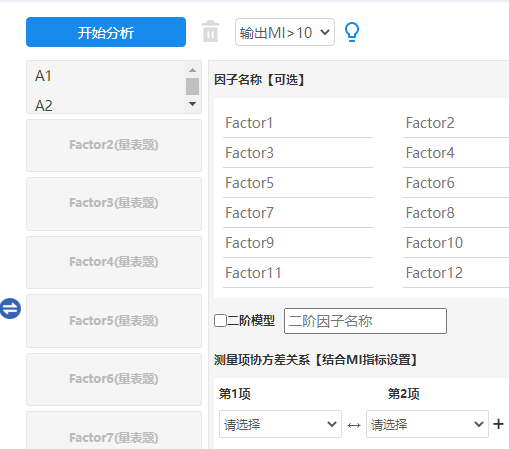
本例子中的量表共分为四个因子,并且按‘MI>10’这一标准输出MI指标结果值,并且默认4个因子的名称为Factro1~Factor4因而不单独设置名称,除此之外,本次案例模型不是二阶模型,因此不选中‘二阶模型’,与此同时,暂不设置‘测量项协方差关系’,最终设置如下图:
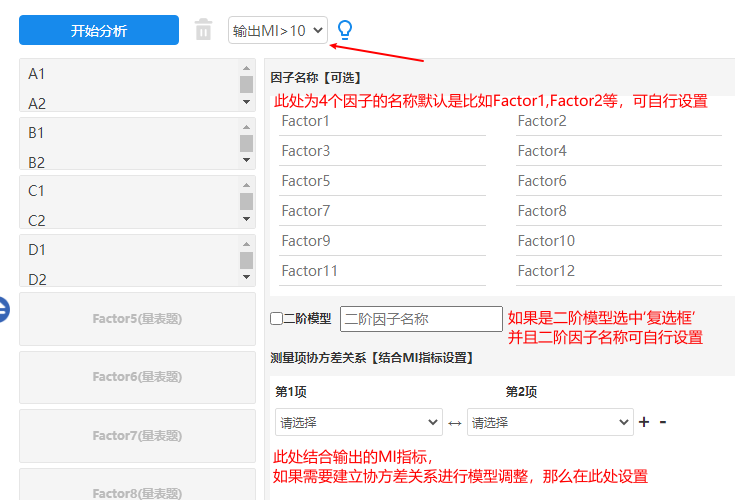
-
4、SPSSAU输出结果
SPSSAU共输出12个表格,分别是CFA分析基本汇总表格,因子载荷系数表格,模型AVE和CR指标结果表格,区分效度:Pearson相关与AVE平方根值表格,模型拟合指标表格,因子和测量项- MI指标表格,测量项间MI指标值表格,因子协方差表格,显变量协方差表格,残差项估计值表格,HTMT(异质-单质比率)结果表格和区分效度指标MSV和ASV表格。关于此6个表格的解释说明如下:
表格 功能用途 备注说明 CFA分析基本汇总 每个因子对应测量项数量汇总 因子对应测量项个数 因子载荷系数 聚合(收敛)效度使用,标准化载荷系数值大于0.7说明具有聚合效度 载荷系数值等 模型AVE和CR指标结果 聚合(收敛)效度使用指标,区分效度使用指标 AVE和CR指标值
AVE平方根值和相关系数区分效度:Pearson相关与AVE平方根值 区分效度使用指标 AVE平方根值和相关系数 模型拟合指标 模型拟合情况,共同方法偏差使用等 各拟合指标值 因子和测量项 - MI指标 因子与测量项间关系强弱,用于模型调整辅助判断和分析测量项是否应删除等 MI指标(要求输出且确实有时才会有值) 测量项间MI指标值 各测量项间关系强弱,用于辅助模型调整使用 MI指标(要求输出且确实有时才有值) 因子协方差表格 因子之间的关系强弱,辅助判断模型构建情况 因子间协方差 显变量协方差表格 查看显变量之间的关系强弱,只有设置后才会有结果 显变量间协方差 残差项估计值 残差估计值 残差值无特别意义 HTMT(异质-单质比率)结果 HTMT法区分效度验证使用 HTMT值 区分效度指标MSV和ASV 区分效度指标 MSV和ASV指标 
从上表可知,本次针对共4个因子,以及20个分析项进行验证性因子分析(CFA)分析。本次分析有效样本量为215,超出分析项数量的10倍,样本量适中。
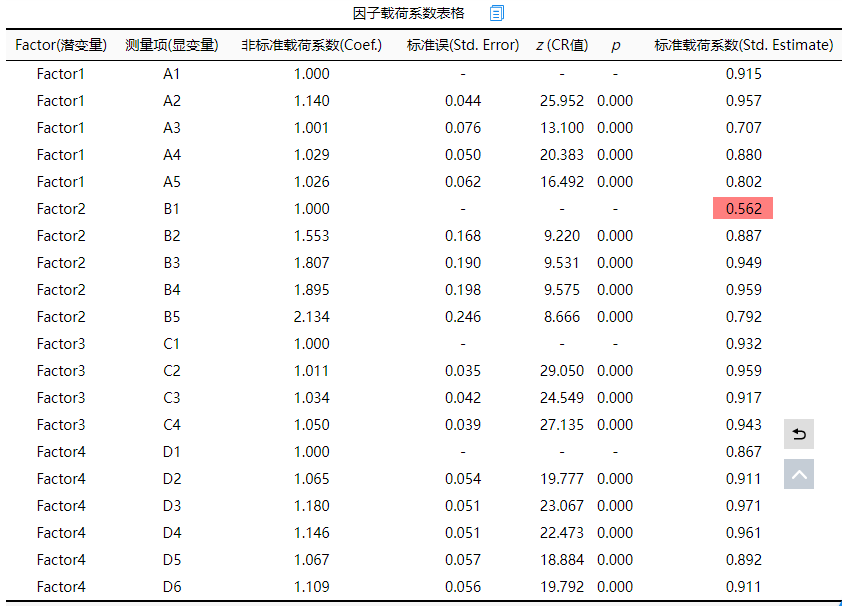
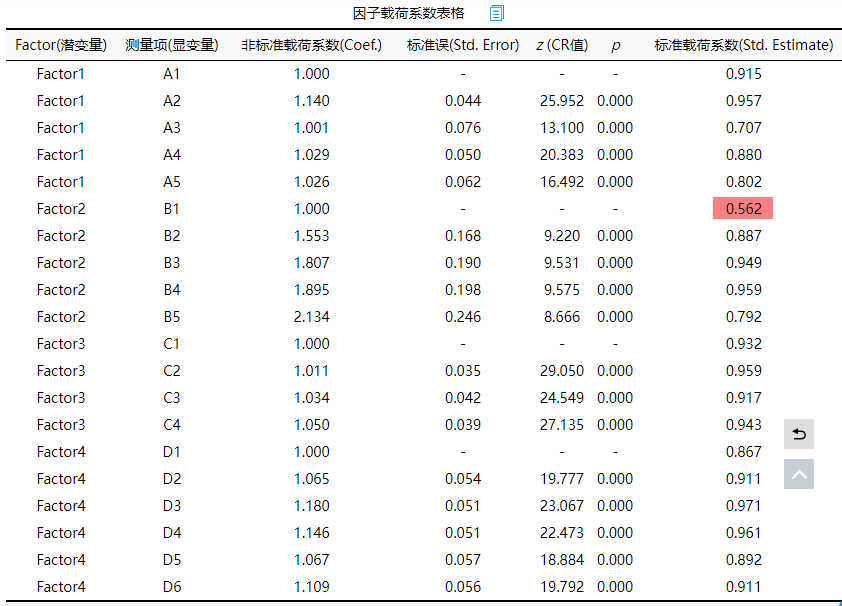
因子载荷系数值表格展示因子和测量项之间的关联关系,一般查看标准载荷系数值进行分析即可。上表格显示,B1与Factor2之间的因子载荷系数值为0.562<0.7,说明对应关系较弱,可考虑将此项从Factor2中移除出去。另外从整体上看,各个测量项全部均呈现出0.001水平的显著性(P<0.001),而且标准化载荷系数值均大于0.7(除B1外),因而说明整体上看,因子与测量项之间有着良好的对应关系,聚合效度较好。另外表格中出现‘-’时意味着该项为参照项因而不会输出。
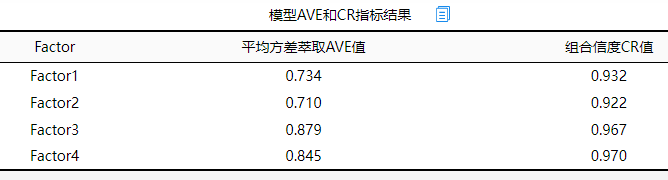
从上格可知:本研究涉及的4个因子(SPSSAU默认给定名字为Factor 1, Factor 2, Factor 3, Factor 4),它们的AVE值全部均大于0.5,而且CR值全部均大于0.7,因而说明本次测量量表数据具有优秀的聚合效度。
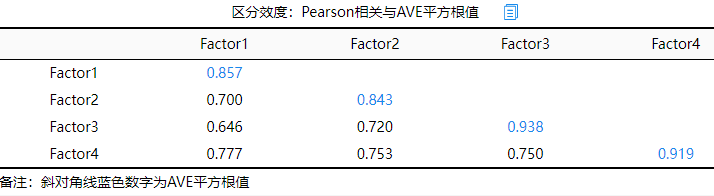
从上表格可知:Factor1的AVE平方根值是0.857,大于其与另外3个Factor之间的相关关系(0.700,0.646,0.777),因而说明其自身的‘聚合性’强于其与‘其它Factor’的关联性,也即说明说明Factor1具有良好的区分效度。除此之外,另外3个Factor也是类似的分析(也得到相同的结论),因而最终说明4个Factor均具有良好的区分效度水平。
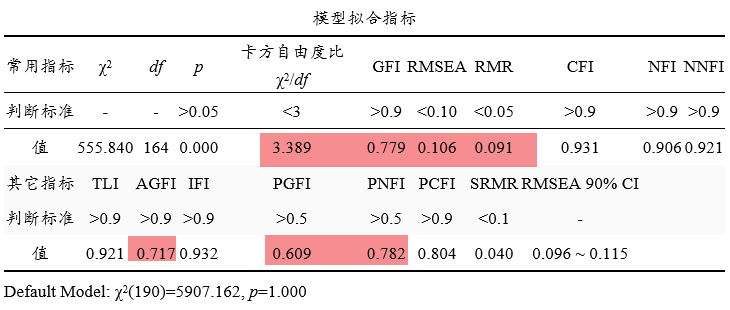
上表格展示模型拟合指标,共分为常用指标和其它指标。常用指标包括卡方自由度比,GFI,RMSEA,RMR,CFI,NFI和NNFI。其它的一些指标通常使用较少,研究人员可结合实际情况进行选择使用即可。
从上表可知:卡方自由度值为3.389,大于3(但小于5),而且GFI小于0.9,RMSEA为0.106接近于0.1这一标准,RMR值为0.091不在标准范围内。综合来看,模型构建欠佳,可能需要模型修正(通常是结合MI指标进行模型修正,下述会说明)。
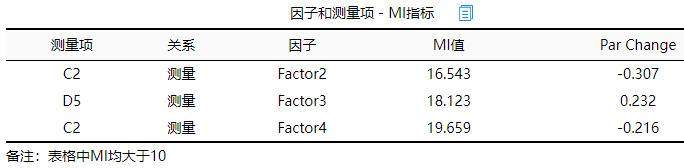
上表格展示因子与测量项的对应关系MI值,因子与其下属测量项的关系可通过因子载荷系数表格进行查看。MI值并不固定标准大小,一般情况下,该值如果大于20则说明关联性很强。从上表格可以看到,C2与Factor2,Factor4这两个因子间的MI指标均大于15,说明C2与Factor2,Factor4之间可能有着较强的关联性;同时,D5与Factor3之间的MI值为18.123,说明二者有较强的关联性。
综合可知:可考虑将C2,D5这两个指标进行删除(即移除出模型),同时上述因子载荷表格分析还发现B1也可以进行删除。因而将此三项进行删除(移除出模型)后可再次进行模型(限于篇幅限制,SPSSAU并不继续进行分析)。
-
特别提示:
-
默认不设置参数,SPSSAU不会输出MI指标值,如果需要则下拉选择输出比如‘MI>10’,即含义为把MI大于10的数据输出;
-
本案例时让SPSSAU输出‘MI>10’的项,也可以选择比如只输出大于50,大于20等。以及如果表格中没有数据,则说明MI指标均小于该参数值因而无数据。
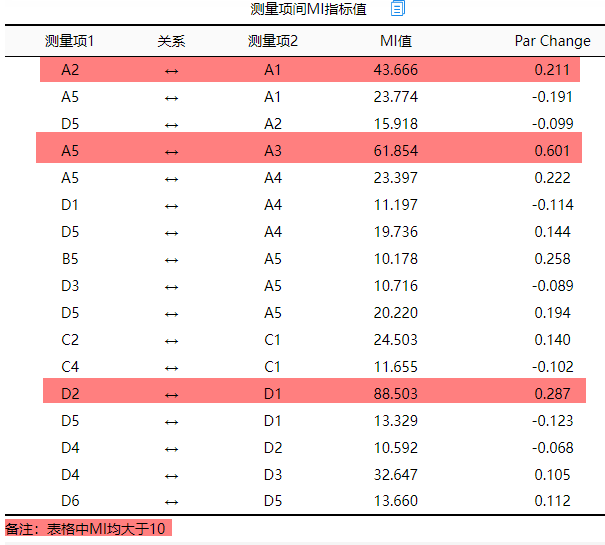
上表格展示测量项间的MI值,其意义为测量项之间的相关关系大小情况。从上表格可以看到,A2和A1,A5和A3,D2和D1这三组之间的MI值很大(此处大和小是相对值,通常结合实际情况综合来回判断没有固定标准),因而如果需要修正模型,可建立该3组之间的‘测量项协方差关系’。
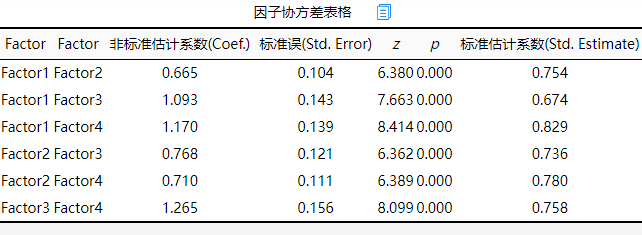
上表格展示因子与因子之间的关联性,可通过标准系数进行分析。从上表可知,在进行因子协方差表格分析时,本研究共4个因子,他们两两之间的标准系数值均介于0.6~0.85之间,说明因子之间具有较强的关联性。

显变量协方差表格用于展示显变量之间的协方差关系情况,上表格并没有结果,这是由于模型并没有进行调整,没有设置过‘测量项协方差关系’,因而不会有结果,如果有过设置,则展示出显变量之间的协方差关系情况,该表格结果值通常并不特别意义。
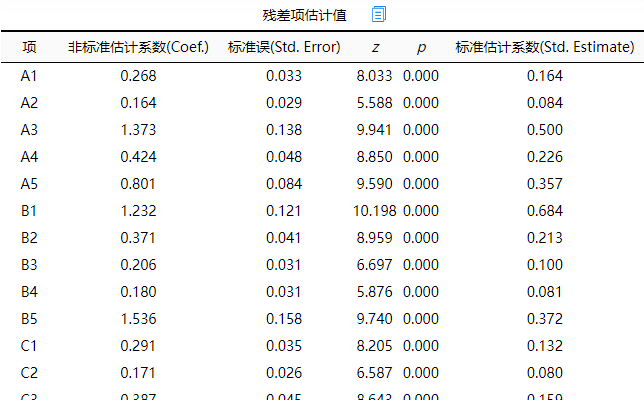
残差项估计值表格,展示出各项的残差估计信息,并不特别意义,有些软件比如AMOS软件会将残差估计值默认展示在模型图中,但SPSSAU当前并没有在模型图中展示残差估计值,如果研究者自行绘制模型图,可使用上表格数据信息进行处理。
-
-
5、聚合(收敛)效度分析
在使用聚合(收敛)效度分析时,一般需要分析以下指标,分别AVE和CR值,以及因子载荷系数值,有时还可分析下模型拟合指标(可选)。
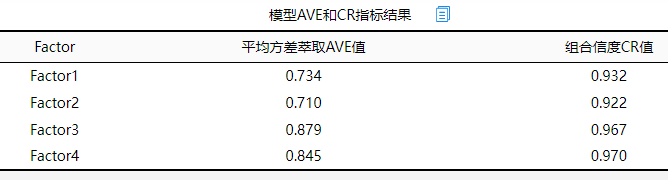
从上表格可知,本次研究量表共由4个因子表示,分别四个因子对应的AVE值全部均大于0.7,最小是0.710,明显高于0.5这一标准;而且组合信度CR值均大于0.9,明显高于0.7这一标准。因而说明本次研究量表具有优秀的聚合效度。而且下表中的因子载荷系数表格显示,4个因子共对应着20个测量项,仅一个测量项的标准化载荷系数值小于0.7,其余项的载荷系数值均接近或者高于0.8,因而综合说明本研究量表数据具有优秀的聚合效度。
-
特别提示:
-
聚合效度通常是针对AVE,CR,因子载荷系数这三个指标进行分析,并且均是在模型最终确认后的指标进行分析;
-
有时候也会对模型拟合情况进行分析说明,建议研究人员以参考文献为准。
-
-
6、区分效度分析
区分效度的测量通常有3种方式。分别是:AVE平方根值与相关系数比较法, HTMT值法, MSV和ASV指标法。
‘AVE平方根值与相关系数比较法’是使用AVE的平方根值,然后与4个因子的相关系数进行对比,如果AVE平方根值大于“该因子与其它因子间的相关系数”,此时说明具有良好的区分效度。AVE平方根值可表示该因子的‘聚合性’,而相关系数表示相关关系,如果该因子自己‘聚合性’很强(明显强于与其它因子间的相关系数),则能说明具有区分效度。
区分效度首先需要进行相关分析(以及每个因子对应多项,需要使用‘生成变量’功能将其概括成一个整体后再进行两两相关分析)。如下:
因子间Pearson相关分析结果 因子1(A1~A5) 因子2(B1~B5) 因子3(C1~C4) 因子4(D1~D6) 因子1(A1~A5) 1 因子2(B1~B5) 0.700** 1 因子3(C1~C4) 0.646** 0.720** 1 因子4(D1~D6) 0.777** 0.753** 0.750** 1 *p <0.05 ** p <0.01 常见的区分效度分析时,会将上表格中斜对角线的1,换成AVE值的平方根,然后再进行对比分析。最终如下表格式:
区分效度:Pearson相关与AVE根值 因子1(A1~A5) 因子2(B1~B5) 因子3(C1~C4) 因子4(D1~D6) 因子1(A1~A5) sqrt(0.734)=0.857 因子2(B1~B5) 0.700** sqrt(0.710)=0.843 因子3(C1~C4) 0.646** 0.720** sqrt(0.879)=0.938 因子4(D1~D6) 0.777** 0.753** 0.750** sqrt(0.845)=0.919 *p <0.05 ** p <0.01 斜对角线数字为该因子AVE的根号值 上图可知,因子1的AVE根号值为0.857,大于因子1与另外3个因子之间的相关系数值(最大为0.777);因子2的AVE根号值为0.843,大于因子2与另外3个因子之间的相关系数值(最大为0.753);类似地,因子3的AVE根号值,因子4的AVE根号值均大于它们与其它因子的相关系数值。因而说明研究量表数据的区分效度良好。
-
特别提示:
-
常见的区分效度分析是将AVE根号值与‘相关系数值’进行对比;SPSSAU还提供HTMT值法和MSV/ASV指标法共2种验证区分效度的指标结果,该两种方式使用较频率较低,研究者自行选择使用即可。与此同时,有时候区分效度的验证方法为:“比较多个CFA模型进行分析说明”,建议研究人员以参考文献为准;
-
上述‘AVE平方根值与相关系数比较法’中的相关系数值,SPSSAU默认是将某因子测量项平均然后计算pearson相关系数,其也可为‘因子协方差表格’中的标准化估计系数值,具体以研究者为准。
-
-
7、共同方法偏差(同源方法,CMV)分析
共同方法偏差(CMV)常见有两种验证方式,一种是使用探索性因子分析EFA方法进行检验 (也称作Harman单因子检验方法),即查看把所有量表项进行探索性因子分析EFA时,如果只得出一个因子或者第一个因子的解释力(方差解释率)特别大,通常以50%为界,此时可判定存在同源方差(共同方法偏差),反之说明没有共同方法偏差问题。
如果是使用CFA进行验证;则将所有的测量项(即所有因子对应的测量量表题项)放在一个因子里面,然后进行分析,如果测量出来显示模型的拟合指标,比如卡方自由度比,RMSEA,RMR,CFI等无法达标,则说明模型拟合不佳,即说明所有的测量项并不应该同属于一个因子(放在一起时模型不好),因而说明数据通过共同方法偏差CMV检验,数据无共同方法偏差问题。
本次共有4个因子对应20个测量项,将此20个测量项全部放在一个因子里面进行CFA分析并且得到模型拟合指标,如下图:
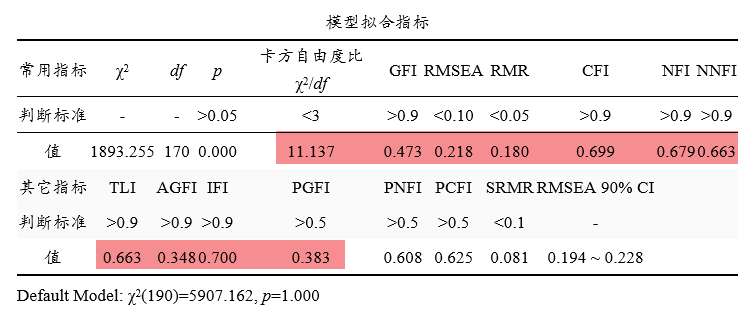
上图显示卡方自由度值为11.137,明显高于标准(>3),并且GFI,CFI,NFI,NNFI这四个指标值全部均低于0.7,明显偏差标准值(大于0.9),RMSEA和RMR值均大于0.15,也严重偏差标准值。其它指标比如AGFI,IFI等也均低于0.7,严重偏差大于0.9这一标准,因而说明模型拟合质量非常糟糕,也即说明不能本次研究量表数据无法聚焦成一个因子,即说明无共同方法偏差问题。
-
特别提示:
-
上述为两种常见的共同方法偏差验证方法,还有其它验证方法,建议研究人员以参考文献为准;
-
研究人员需要在事前注意共同方法偏差问题,而不能等到事后发现共同方法偏差才能处理。
-
-
8、剖析
验证性因子分析CFA分别有三个应用功能,分别具有对应的注意事项,分别如下:
-
如果使用CFA进行聚合(收敛)效度,或区分效度分析,建议首先进行探索性因子分析(EFA),然后再进行CFA分析;原因在于CFA对于数据质量要求高,如果探索性因子分析就发现因子与测量项对应关系出现偏差,需要首先进行处理,确认好因子与测量项对应关系后,再进行CFA分析;
-
如果使用CFA进行分析,建议样本量至少为测量项(量表题)的5倍以上,最好10倍以上,且一般情况下至少需要200个样本。
-
一个因子对应的测量项最好在5~8个之间,便于后续删除掉不合理测量项。
-
聚合效度通常是针对AVE,CR,因子载荷系数这三个指标进行分析,并且均是在模型最终确认后的指标进行分析;
-
聚合效度分析有时候也会对模型拟合情况进行分析说明,建议研究人员以参考文献为准。
-
常见的区分效度分析是将AVE根号值与‘相关系数值’进行对比;有时候区分效度的验证方法为:“比较多个CFA模型进行分析说明”,建议研究人员以参考文献为准;
-
疑难解惑
-
验证性因子分析CFA拟合不达标解决办法?
-
验证性因子分析 CFA 通常是针对成熟量表进行效度验证等;不成熟量表通常使用探索性因子分析(进阶方法->因子分析)进行效度验证(或者问卷研究里面的效度分析)。如果无论如何均出现拟合指标不达标时,建议按以下步骤进行检查:
-
第一步:使用探索性因子分析(进阶方法->因子分析;或者问卷研究->效度分析)查看数据情况,对应关系情况如何等,并且删除掉对应关系与预期不符合的项;直至使用探索性因子分析进行效度验证时,完全问题为止;如果使用探索性因子分析进行效度验证,无论如何均不达标时,那肯定地验证性因子分析不会达标(原因是验证性因子分析对数据质量要求更高);
-
第二步:基本第一步的结论基本上,再进行验证性因子分析。
-
除此之外,建议可按以下2种方式进行模型调整。
-
第1是将载荷系数值较低(比如小于0.6)或者不显著(p 值大于0.05)的项从模型中移除出去;
-
第2是按MI指标调整,首先输出比如MI>10的结果,然后将MI值较大的两两项之间建立"测量项协方差关系"后再次分析。如果模型拟合指标非常糟糕,通常此种处理并不生效,通常只会降低卡方自由度值,对其它指标帮助非常小。
-
关于“二阶”的说明?
-
绝大多数情况下均为一阶验证性因子分析。如果说验证性因子分析时为二阶模型,此时参数处选中‘二阶’即可。关于‘二阶’结构如下图所示:
-
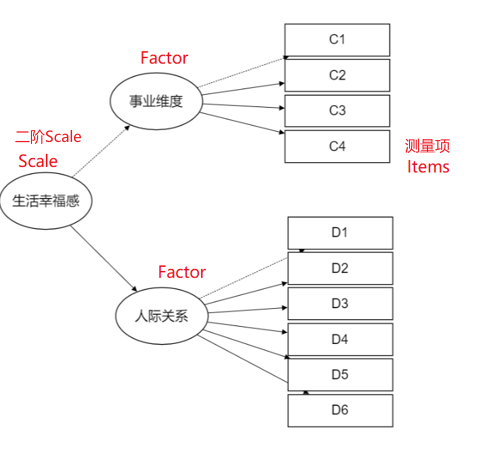
-
聚合效度和区分效度分析问题?
-
对于聚合效度, SPSSAU 默认提供聚合效度分析表格(包括 AVE 和 CR 值);对于区分效度, SPSSAU 默认提供区分效度检验表格,即‘下三角格式的相关系数表格,下三角线为 AVE 的根号值’。
-
最多放12个因子?
-
验证性因子分析是以量表为单位,如果有多个量表则重复进行多次验证性因子分析即可。正常情况下,一个量表仅会对应4~5个因子,更不会超过12 个因子,建议确认是否进行了正确的分析。
-
分析框只能放20项?
-
验证性因子分析时,第1个框(因子1对应的框)最多可放置80项,第2个框(因子2对应的框)最多可放置40项,第3个框(因子3对应的框)最多可放置30项,余下的9个框(因子4~因子12)最多可放置20项。
-
同一个因子(维度)正常情况下只会对应3~7项,如果超出10项,建议检查是否进行了正确的分析。
-
SPSSAU验证性因子分析中如果输出MI值和如何使用它?
-
如果希望SPSSAU输出MI指标值,可在开始分析按钮右侧下拉选择输出MI值,比如‘输出MI>10’,其意义是将MI值大于10的全部输出(通常情况下MI值非常多,但一般只有较大的值才有参考意义)。在输出之后,可将MI值非常大的两两项之间建立‘协方差相关关系’(即相关关系,在‘测量项协方差关系’处进行设置),用于修正模型。MI值的修正通常会让卡方自由度值得到减少,其它指标一般不应该有太大的变化,不能过多的依赖于MI值进行模型修改。
-
提示‘数据质量异常’如何解决?
-
出现此种情况,建议按以下步骤进行检查并解决。
-
第一:相关性过低。同一个因子里面的项应该有很强的相关性才正常。因而建议把同一个因子里面的项做相关分析,如果发现某两项之间的相关性过弱(比如相关系数小于0.2),把其中一项从模型中移除出去,重复进行检查即可;
-
第二:样本量过低,比如总共有5个因子共计20个分析项,但分析样本量仅50个,这会导致模型无法收敛因而最终无法拟合。
-
如何提高AVE和CR值?
-
如果出现AVE或者CR值无法达标时,此时建议按以下步骤进行检查并解决。
-
第一:移除掉载荷系数值较低的项,一个移除一个多次尝试;
-
第二:检查是否某个分析项的MI值过高,可考虑移除此项分析项;
-
第三:结合MI指标值进行模型调整;
-
第四:考虑以一个因子作为单位,重复多次进行CFA分析,模型越简单时效果相对会更好;
-
第五:加大样本量,一般情况下样本量越大模型拟合效果越佳。
-
HTMT(异质-单质比率)是什么?
-
验证性因子分析可用于区分效度检验,共有两种检验方法,一是使用AVE平方根与相关系数对比法;另一种是HTMT法;通常情况下使用AVE平方根法较多,HTMT法使用相对较少;如果说HTMT值全部均小于0.9,此时说明数据具有区分效度。
-
区分效度不达标如何办?
-
区分效度用于检验因子与因子之间具有区分性,如果出现区分度不好时,通常是由于出现‘错位’现象,比如Factor1里面有5个量表题,很可能其中2个题放在Factor2里面更适合。一般是结合载荷系数值判断出此类题,然后删除掉此类题(或者进行移位)即可。
-
残差值估计值有什么作用?
-
该指标值通常无实际意义,只是模型拟合后产生的残差值而已。
-
残差值无实际意义,SPSSAU的模型图里面默认没有提供残差值,但输出表格里面有。如果需要可自己手工作图处理。
-
验证性因子分析使用的估计方法是?
-
SPSSAU默认使用最大似然法ML进行模型估计。
-
模型拟合度里面自由度为0?
-
模型拟合度出现自由度为0是正常现象,并且此时无法计算得到卡方值,卡方自由度值等,此时直接不关注对应的指标即可。出现自由度为0的原因通常是模型过于简单,或者模型过于‘饱和’,可能是非递归模型所致。
-
标准化载荷系数值大于1?
-
如果标准化载荷系数值大于1,通常是由于出现共线性问题所致;建议可通过相关分析查看相关系数,如果某具体项之间的相关系数值非常高,可考虑移除该项;如果共线性不严重,通常并不需要移除。
-
图里面的虚线代表什么意思?
-
SPSSAU默认以放置顺序的第一项作为参考项,图里面的虚线标识出该项为参考项。参考项的非标准载荷系数值一定为1,而且不会有标准误值等。
-
分析项超过60个不进行MI指标输出和自动按MI指标建模什么意思?
-
如果说分析项(显变量)的个数大于60个,SPSSAU默认不会输出MI指标值,并且如果用户要求进行按MI指标调整模型,SPSSAU也不会进行模型调整。
-
z 值和临界值或t 值的意义?
-
验证性因子分析时,SPSSAU输出z 值,该值与AMOS软件等的临界值CR或t 值意义完全一致。
-
标准化载荷系数大于1?
-
标准化载荷系数值通常应该小于1,如果出现大于1,很可能是由于共线性问题所致,建议做相关分析,将相关关系非常大(比如大于0.7)的项移除后再次分析。
-
CFA如何输出MI指标值?
-
进行验证性因子分析时,可在开始分析按钮右侧“MI指标输出”下拉,选择输出MI指标值。如果需要结合MI指标情况进行模型调整,那么可在测量项协方差关系’时设置具体测量项之间的相关关系(协方差关系)即可。MI值越大意味着可减少的卡方值越多,结合该指标进行模型调整时,一般会对卡方自由度值有着较大的帮助。
-
CFA每个框最多可放多少项?
-
验证性因子分析时,需要设置因子与测量项的对应情况,一个因子通常对应4~7个测量项。SPSSAU系统中,第1个因子框最多可放置80个测量项,第2个因子框最多可放置40个,第3个因子框最多可放置30个,其余每个因子中放置的测量项个数最多为20个。
-
CFA如何进行模型独立性检验?
-
如果希望使用验证性因子分析CFA进行区分效度检验,有几种做法,SPSSAU默认提供AVE根号值与相关系数判断法(Fornell-Larcker),HTMT法,以及独立性检验法。独立性检验法需要研究者自行设置多个不同的CFA模型,然后对比不同的CFA模型拟合指标效果情况,并且判断得出最佳的模型,用于证明模型间的独立性情况。比如下表格:
| 编号 | 模型 |
| M0 | 3因子模型:因子1,因子2,因子3 |
| M1 | 2因子模型:因子1,因子2+因子3 |
| M2 | 2因子模型:因子2,因子1+因子3 |
| M3 | 1因子模型:因子1+因子2+因子3 |
-
某量表共有3个因子,默认是希望M0模型即3因子模型,即量表分成3个因子,每个因子对应着一些测量项(M0)。那么此种结构是否最优呢?可通过对比不同的模型结构(通过拟合指标,通常仅几个常见指标对比)来判定。比如上表格中用了另外3种测量结构(M1~M3)来进行对比,M1结构时,仅有两个因子,因子1的测量项单独占用1个因子,因子2和因子3全部的测量项占用1个因子(因子2和因子3对应的测量项全部放在1个因子框里面);类似M2结构也一样。M3结构时,因子1,因子2和因子3所有的测量项全部占用1个因子(即把所有的测量项全部放在一个因子框里面)。
-
SPSSAU默认提供MSV值(maximum of shared squared variance )和ASV值(average of shared squared variance)值,该2个指标可用于区分效度分析(区分效度还可使用Pearson相关与AVE值对比法),一般情况下MSV和ASV值均小于AVE值则说明具有较好的区分效度。
SPSSAU进行MSV和ASV?
-
探索性因素分析(Exploratory Factor Analysis,EFA)和因子分析,在SPSSAU中是完全相同的意思。
探索性因素分析和因子分析的区别?
-
SMC值=标准化载荷系数loading值的平方,可通过标准化载荷系数直接计算即可。SMC(Square Multiple Correlation)指标值理论上应该介于0到1之间,该值越大意味着测量项与因子间的关系越为紧密,一般SMC指标大于0.5即可(此时标准化载荷系数值约为0.71)。
验证性因子分析时,SMC值如何计算?
-
SPSSAU进行验证性因子分析区分效度时,默认提供pearson相关系数,研究者也可以使用‘协方差表格’中的协方差相关关系系数。
验证性因子分析的区分效度表格中相关系数不一致?
-
模型是由系统自动绘制,通常情况下建议先对标题进行简化后再进行分析。比如标题简化为A1,A2,A3,B1,B2,B3,满意度1,满意度2,满意度3等。可通过SPSSAU数据处理->标题处理,批量修改标题名称。
标题过长模型不美观如何图形?
-
SPSSAU暂没有提供二阶因子的AVE和CR值,可自行结合输出结果进行计算。两个指标的计算公式分别如下,AVE=Average(Sum(loading平方)),loading是标准化载荷系数,Sum是求和的意思,Average是求平方值,简言之即标准化载荷系数平方后求和,接着取平均值。CR=Sum(|loading|)^2 / [Sum(|loading|)^2 + Sum(e)], 其中e为残差其等于1-标准化载荷系数的平方,简言之即分子为loading(取绝对值防止正负向抵消)求和后平方,分母为分子值加上残差值。
如何计算二阶因子的AVE和CR值?
-
如果仅2个factor时,即使选中二阶模型,也会是一阶模型,因为2个factor只拉取该2项的关系情况,其是一种特殊的结构。
SPSSAU中进行验证性因子分析时选中了二阶模型但没有出现二阶?
-
SPSSAU进行CFA分析绘制模型图时,模型图中默认没有提供残差项,研究者可下载模型图手工进行绘制或者忽略(默认情况下残差项从分析视角上无实际意义)。
