Power功效分析之均值差
Power功效分析常用于实验研究时样本量的计算(或功效值计算),实验研究中均值差的使用较多,具体包括单样本t检验、独立样本t检验、配对t检验、单样本z检验、Mann-whitey检验和配对符号秩和检验等,具体如下表格所述:
| 名词 | 说明 |
|---|---|
| 单样本t检验 | 对比平均值与某数字的差异 |
| 独立样本t检验 | 对比两个平均值差异 |
| 配对t检验 | 对比两个配对数据的平均值差异 |
| 单样本z检验 | 对比平均值与某数字的差异 |
| Mann-whitey检验 | 对比两个平均值的差异 |
| 配对符号秩和 | 对比两个配对数据平均值的差异 |
接着以独立样本t检验为例进行说明,其研究两组数据的均值差异,比如实验组和对照组的均值差异,那么预期(或者以往实验/以往文献)有着两组数据的平均值和标准差数据,并且基于预定好的alpha值和power值,此时样本量应该多少适合呢?也或者有着两组数据的平均值和标准差数据,基于设定好的alpha值和样本量,此时power水平如何呢?
即在SPSSAU中,共包括两项功能,分别是计算样本量和计算功效Power值,具体涉及到Power功效原理,可查阅‘Power原理’内容。接下来具体讲解操作,如下所述:
-
1、关于分析Power值
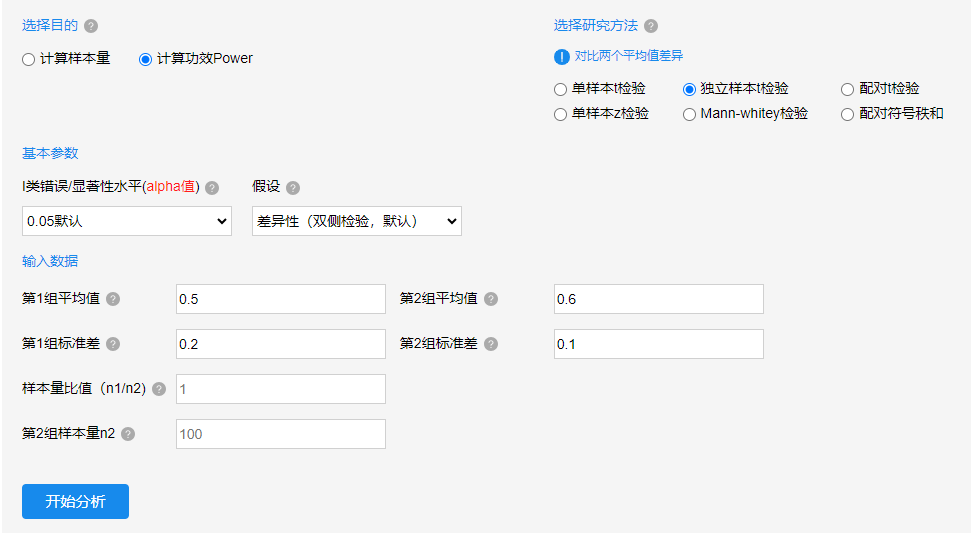
上图中目的在于计算Power值,并且研究为独立样本t检验,两组数据的平均值分别是0.5和0.6,标准差值分别是0.2和0.1,并且alpha值为默认的0.05,使用默认的双侧检验,共有两组数据,第2组样本量n2=100,并且第1组样本量除以第2样本量即n1/n2=1,那么第1组样本量也是100。即基于两组均为100样本量前提下,且两组数据的平均值和标准差确定前提下,alpha值确定下。那么此时的功效水平如何呢?‘错的说成错说’这一情况的概率是多少呢?最后点击开始分析,结果如下所示:

计算结果显示,基于I类错误为0.05,两组数据样本量均为100,且两组数据的平均值和标准差值等均确定前提下,最终的功效Power值是0.994,即‘错的说成错的’即‘H0为假并且最终判断成假’这一情况的概率是99.4%,即对‘错的说成错的’这一情况有着很高的把握度。
-
2、关于分析样本量
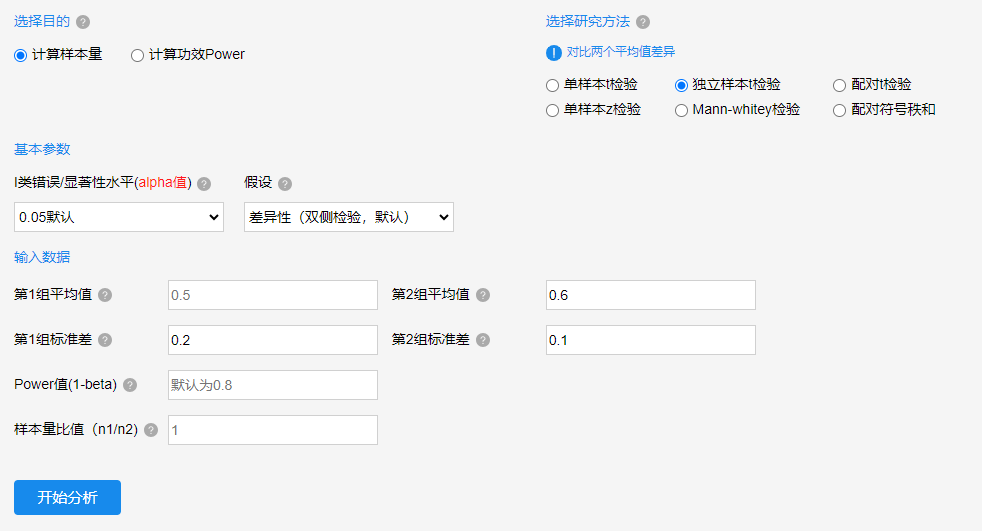
上图中目的在于计算样本量,并且研究为独立样本t检验,两组数据的平均值分别是0.5和0.6,标准差值分别是0.2和0.1。并且alpha值为默认的0.05,使用默认的双侧检验,Power为默认的0.8,即有80%的把握‘错的判断成错的’(也即‘错的说成对的’的概率是20%)。那么基于上述前提下,此时两组样本量应该多少较为适合,才具有科学性呢?两组样本量有个参数为‘样本量比值 n1/n2’,其默认为1即说明第1组和第2组的样本量一致,当然也可以设置为2,那意味着第1组的样本量是第2组样本量的2倍。最后点击开始分析即可,结果如下:

计算结果显示,基于I类错误为0.05,II类错误为0.2,Power值为0.8前提下,要想达到上述研究的差异具有科学判断性,此时第1组和第2组样本量均为41即可。
-
1、剖析
-
涉及以下几个关键点,分别如下:
-
均值差的意思是计算平均值的差异,在SPSSAU功效分析时,其共包括6项分别是单样本t检验、独立样本t检验、配对t检验、单样本z检验、Mann-whitey检验和配对符号秩和检验。具体应该选择哪个方法应该以实际研究为准即可。
-
-
2、疑难解惑
-
如何理解alpha值和power值?
-
I型错误研究‘对的说成错的’的概率,一般最大取0.05,那么此0.05即为alpha值即显著性水平值。II型错误研究‘错的说成对的’的概率,一般最大取0.2,那么此0.2即为beta值,那么Power值=1-beta值即0.8,其则表示为‘错的说成错的’的概率。
-
更多关于Power功效的原理,可具体参考‘Power原理’帮助手册。
-