Power功效分析之广义模型
Power功效分析常用于实验研究时样本量的计算(或功效值计算),如果是涉及广义模型时的回归系数差异计算时,SPSSAU共提供二元logit回归和Poisson回归情况时的Power功效分析,具体如下表格所述:
| 名词 | 说明 |
|---|---|
| 二元Logit回归 | 二元Logit回归时回归系数差异的功效分析 |
| Poisson回归 | Poisson回归时回归系数差异的功效分析 |
比如二元Logit回归时,对比某个自变量X回归系数的差异情况,此时则使用‘二元Logit回归’,当然如果研究时使用的是Poisson回归,也是对比某X回归系数的差异情况,此时使用‘Poisson回归’。
SPSSAU进行功效分析时,共包括两项功能,分别是计算样本量和计算功效Power值,具体涉及到Power功效原理,可查阅‘Power原理’内容。接下来以‘二元Logit回归’为例具体讲解操作,如下所述:
-
1、关于分析Power值
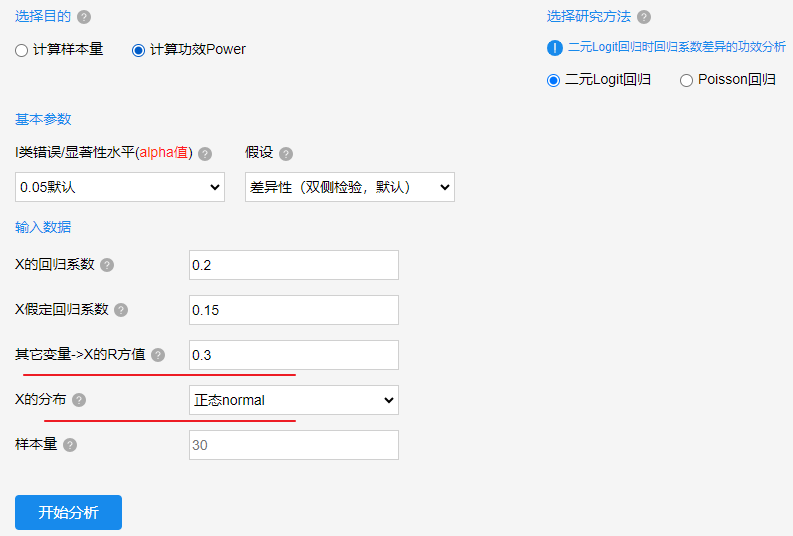
上图中目的在于计算Power值,其研究二元Logit回归时,某变量的回归系数是否明显与某数字有明显差异性。图中显示alpha值为0.05,并且二元Logit回归时得到X的回归系数是0.2,其需要与0.15进行对比。与此同时,二元Logit回归模型时还有另外的变量,另外的变量对于X进行线性回归时得到的R 方值为0.3。并且X的分布基于正态分布前提,除此之外,当前是基本30个样本量进行二元Logit回归,最终结果如下所示:

计算结果显示,基于I类错误为0.05,线性回归样本量为30时,最终得到Power值为0.070,即不犯II类错误的概率是7%,即说明仅有7%的把握‘错的说成错的’。说明当前较小的回归系数差异(0.2和0.15),在30个样本时的Power功效能力非常弱。
-
2、关于分析样本量
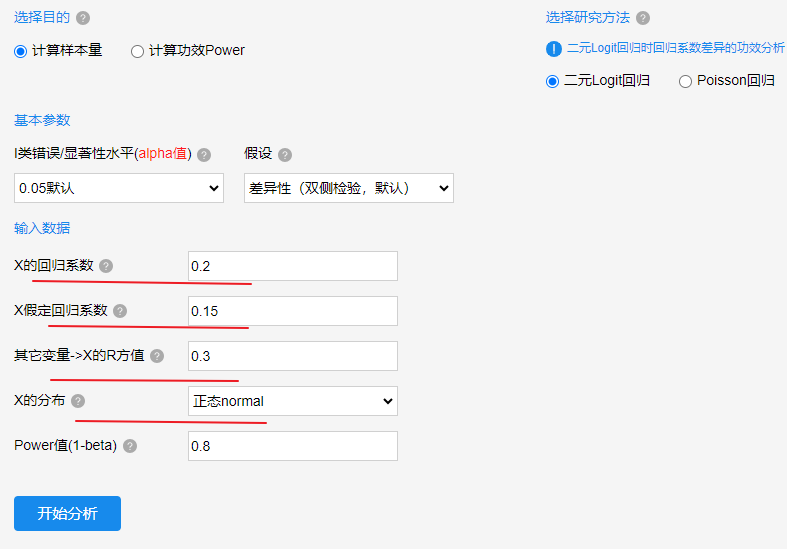
上图中目的在于计算样本量,研究基于alpha值为0.05,Power为0.8,并且二元Logit回归时X的回归系数是0.2(其需要与0.15进行对比),与此同时,二元Logit回归的其它自变量对于X做线性回归时的R 方值是0.3,且X假定为正态分布前提时。最后点击开始分析即可,结果如下:

计算结果显示,基于I类错误为0.05,II类错误为0.2,Power值为0.8前提下,要想达到上述研究具有科学判断性,此时在样本量为1150.880即向上取整为1151个样本时,该研究才能具有0.8的功效能力,即需要很大的样本量才能较为敏锐的检测出0.05的回归系数差异。
-
1、剖析
-
涉及以下几个关键点,分别如下:
-
SPSSAU中进行二元Logit回归或者Poisson回归时的Power功效分析时,其涉及到的参数较多,包括回归系数,其它的变量对研究项做回归时得到的R 方值,以及X的分布假定情况等,建议研究者提前作好参数准备。
-
-
2、疑难解惑
-
如何理解alpha值和power值?
-
I型错误研究‘对的说成错的’的概率,一般最大取0.05,那么此0.05即为alpha值即显著性水平值。II型错误研究‘错的说成对的’的概率,一般最大取0.2,那么此0.2即为beta值,那么Power值=1-beta值即0.8,其则表示为‘错的说成错的’的概率。
-
更多关于Power功效的原理,可具体参考‘Power原理’帮助手册。
-