Power功效分析之方差
Power功效分析常用于实验研究时样本量的计算(或功效值计算),实验研究中进行方差分析的情况较多,在SPSSAU中单独将方差放成一个计算Power的方法,其具体包括单因素方差/双因素方差和多因素方差,具体如下表格所述:
| 名词 | 说明 |
|---|---|
| 单因素方差 | 研究1个因子各组别平均值差异 |
| 双因素方差 | 两个因子时的方差分析 |
| 三因素方差 | 三个因子时的方差分析 |
无论是单因素/双因素或者三因素方差,均可加入协变量个数这一参数信息,默认没有协变量即为0个协变量。除此之外,其还需要提供效应量参数值即偏Eta方(Partial η2) ,偏Eta方=组间差SSB/总离差SST,在SPSSAU中,如果是单因素方差默认有输出偏Eta方(Partial η2),如果是双因素方差和三因素方差,此时需要选中‘效应量’参数才会输出该指标值。
SPSSAU进行功效分析时,共包括两项功能,分别是计算样本量和计算功效Power值,具体涉及到Power功效原理,可查阅‘Power原理’内容。接下来以‘单因素方差’为例具体讲解操作,如下所述:
-
1、关于分析Power值
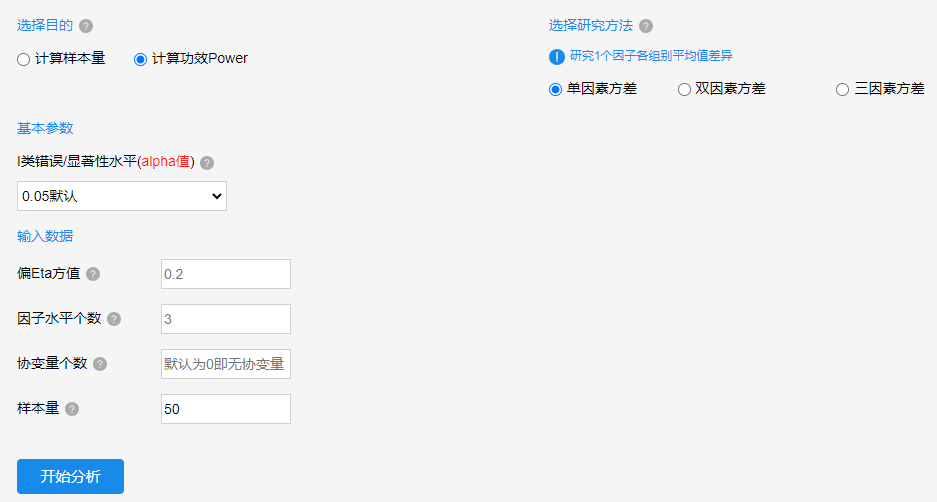
上图中目的在于计算Power值,并且研究为单因素方差,无协变量(协变量个数为0),并且效应量指标偏Eta方值为0.2,单因素方差的自变量X有3个水平,此时基于样本量为50时,想了解对应的Power值是多少,即此时‘错的说成错的’这种情况的概率是多少,结果如下所示:

计算结果显示,基于I类错误为0.05,样本量为50的单因素方差(不带协变量),则效应量指标偏Eta方值为0.2前提时,计算得到的Power值为0.875,即‘错的说成错的’这种情况的概率是87.5%>常见默认标准80%,因而意味着当前研究具有较高科学性。与此同时,SPSSAU还输出样本量和Power的关系示意图,可通过该图直观查看样本量与Power之间的关系情况,如下:
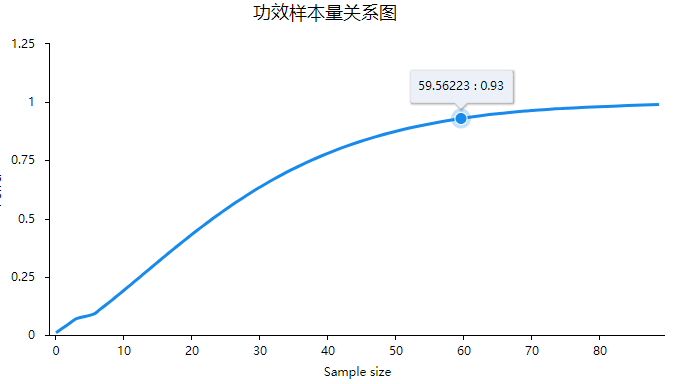
上图中横坐标是样本量,纵坐标是Power值,明显地可以看到,随着样本量的增加,Power值也会增加。这是二者默认的逻辑关系。从图中还可看到,当样本量为59.56223向上取整为60时,此时的Power水平为0.93。
-
2、关于分析样本量
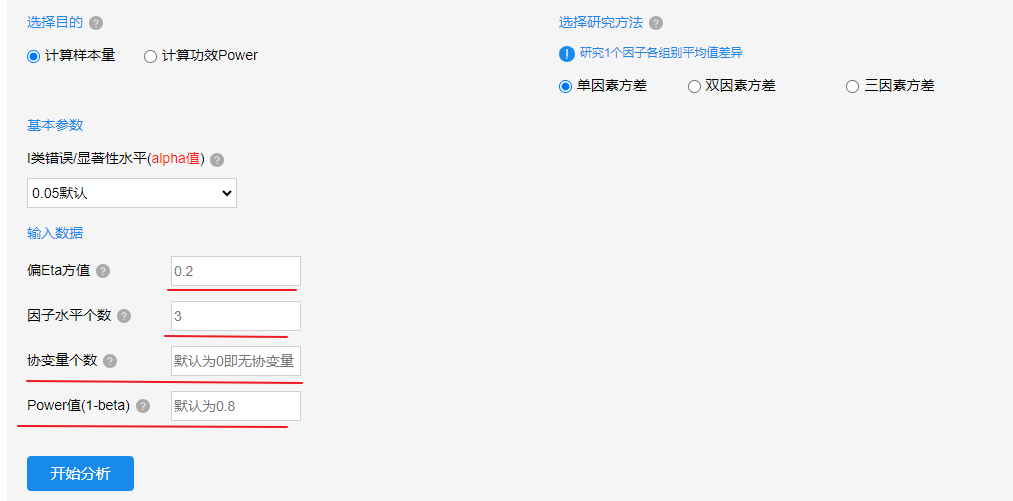
上图中目的在于计算样本量,并且研究为单因素方差,基于显著性水平alpha值为0.05,效应量偏Eta方值为0.2,并且单因素方差时没有协变量(即协变量个数为0),与此同时,单因素方差时X对于Y的差异,X是定类数据且有3个水平(比如低/中/高),基于Power值为0.8水平时,此时应该多少样本量才能达到一种科学性平衡呢。最后点击开始分析即可,结果如下:

计算结果显示,基于I类错误为0.05,II类错误为0.2,Power值为0.8前提下,要想达到上述研究的差异具有科学判断性,此时需要研究样本量为41.686个,向上取整后为42个样本。除此之外,SPSSAU还输入功效与样本量的关系示意图,如下:
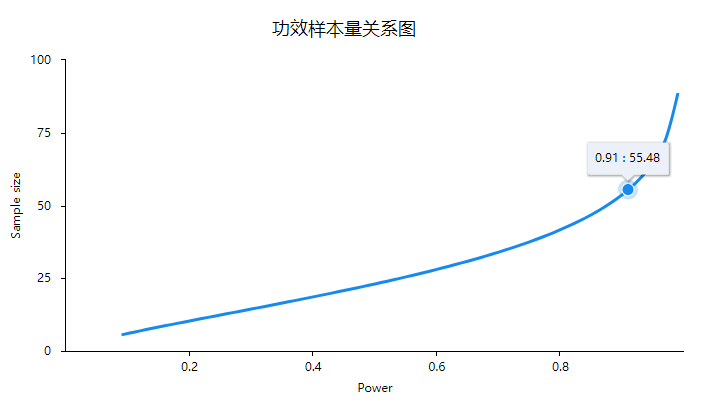
上图展示Power和样本量的关系,横坐标是Power值,纵坐标是样本量,明显的二者关系是递增关系,从图中可以看到比如当Power值为0.91时,此时需要样本量为55.48即56个。研究者可通过该图示查看和了解,研究需要的Power信息前提下需要多少对应的样本量。
-
1、剖析
-
涉及以下几个关键点,分别如下:
-
SPSSAU中进行Power功效分析时,如果是方差分析时,其需要提供偏Eta方这个效应量指标,该指标在SPSSAU的分析方法中均能找到。
-
-
2、疑难解惑
-
如何理解alpha值和power值?
-
I型错误研究‘对的说成错的’的概率,一般最大取0.05,那么此0.05即为alpha值即显著性水平值。II型错误研究‘错的说成对的’的概率,一般最大取0.2,那么此0.2即为beta值,那么Power值=1-beta值即0.8,其则表示为‘错的说成错的’的概率。
-
更多关于Power功效的原理,可具体参考‘Power原理’帮助手册。
-