二元logistic回归数学原理

  • 1、二元logistic回归模型构建

    大家都知道，二元logistic回归时，其实际分析上是研究X对于 Y 的影响，而且 Y 为二分类数据，比如是否愿意购买产品，是否喜欢，是否购买直播带货商品等。数字1代表YES，数字0代表NO。而且 X 对于 Y 的影响时，数学模型可构建如下：

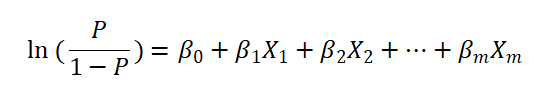
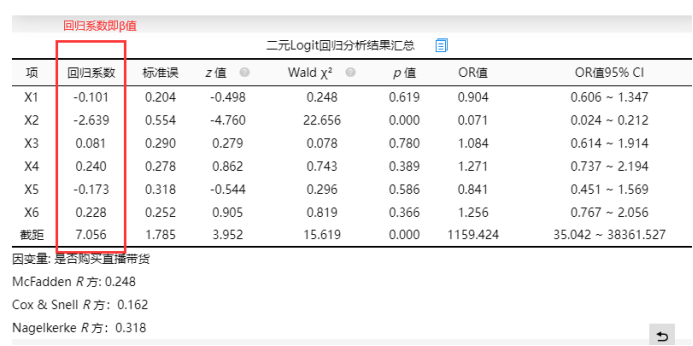
    上式中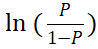，服从二元logistic分布，P 表示发生的概率，1-P 表示没有发生的概率，研究的数据 Y 只会有数字1和0，所以使用模型构建时，也希望本来原始数据是1，那么模型拟合出来的预测值也尽最大可能接近1，本来原始数据是0，那么模型拟合出来的预测值也尽最大可能接近0。而且等号右侧的X1，X2等均为研究的X即影响因素。β代表估计参数，分析上称其为回归系数。如果与SPSSAU结果对应则如下：

    本案例数据，可点击下载

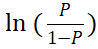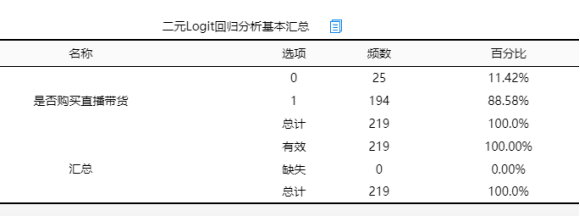
    上述中的回归系数值，即为二元logistic回归需要计算出来的值。那么该值是如何计算得到的呢？首先：模型等式左边即，P 表示发生的概率，1-P 表示没有发生的概率，研究的数据 Y 只会有数字1和0，所以使用模型构建时，也希望本来原始数据是1，那么模型拟合出来的预测值也尽最大可能接近1，本来原始数据是0，那么模型拟合出来的预测值也尽最大可能接近0。这是可以直接想到的，但如何估计得到呢？

    这里使用到了数学上的“极大似然法”原理，即：当前比如有219个样本数据（219行），那么就有219个 Y 值，而且219个 Y 值里面有的是数字1，有的是数字0，比如本文档使用的数据 Y 为‘是否购买直播带货’，其中有194个为数字1即购买过直播带货，25个没有购买过直播带货（数字为0）。既然出来了这样的结果，那么就说明当前这种情况（194个为yes，25个为no），这种情况并非偶然而一种最大的可能（似想为什么没有出现比如100个yes和94个no呢？），这种思想就称为“极大似然法”。接下来一部分将单独讲解“极大似然法”。

  • 2、极大似然法

    接着上一部分，共有219个样本数据，对于‘是否购买直播带货’这个 Y ，其中194个为yes，25个no。这种情况的产生并非偶然而是基于当前的6个影响因素X，对于 Y 会产生影响，因而出现了此种情况（其中194个为yes，25个no）。正是由于6个影响因素对于‘是否购买直播带货’这个 Y 的影响，出现当前最大的可能（其中194个为yes，25个no）。

    那么循着当前的“最大似然法”思维，构建出数学公式如下：

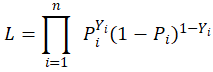
    上式中，i代表219个样本的编号，n=219，i是遍历编号。P 代表模型最终预测的概率，1-P 代表残差。Y 表示 Y 的取值（0或1）。明显可以看出：如果 Y 为1，那么就为P ，如果 Y 为0，那么就为1-P 。上一部分中已经说到，肯定希望 Y 为1的时候模型拟合得到的也尽可能为1， Y 为0的时候模型拟合得到的也尽量接近0。那么即使如此，也就说希望上式L 能得到最大值最好了。

    继续对上式取对数后，得到如下公式即：

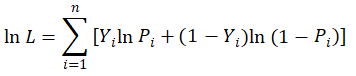
    也即将L 取最大值，转换成求ln L 的最大值就好。上式中 Y 值为已知数据（即原始数据），P 是模型需要拟合的数据，而且P 值的计算公式可以结合下式进行转换：

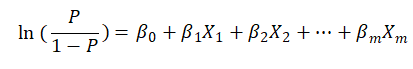
    将上式转换后得到如下：

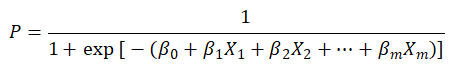
    β代表估计参数，即SPSSAU输出的回归系数。β0为常数项即SPSSAU中的截距项。即最终转换成，让待估计参数（回归系数）估计，而且估计得到的ln L 最大。即让ln L 最大时得到的回归系数，即为最终模型的回归系数。

    那么如何求解得到回归系数呢？当前已知有219行样本数据，而且知道要求解ln L 的最大值，ln L 为最大值时对应的P 值就是最优，而且P 值又是由待估计参数（回归系数）决定，因此求解最优回归系数（即最终解）则成为接下来第3部分的内容。

    另外，SPSSAU系统中选择‘保存残差和预测值’，得到的预测值即为P 值，残瑳值即为1-P 值。如下图操作：

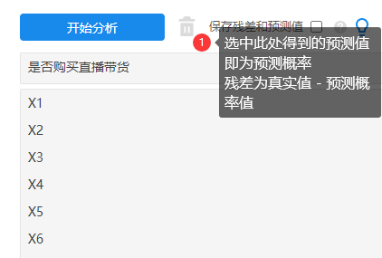
  • 3、Newton牛顿迭代法

    上一部分讲到，数学模型上ln L 的最大值时，得到的估计参数即为模型求解得到的最终回归系数。那么如何求解回归系数呢？数学上有很多种求解方法，包括比如：Newton牛顿迭代法，BFGS法（拟牛顿法），lbfgs法等等。这种方法均是求解最优问题的解决方式。最优问题正如二元logistic回归时，需要求解ln L 的最大值时得到最终回归系数一样。接下来将简要说明下Newton牛顿迭代法。高等数学中有讲到过求解最大值时，使用切线，或者求导数为0，接着本部分简要说明下：

    首先求解某个函数的极值时，很容易想到泰勒展示式，如下式：

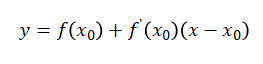
    接着令上式为0，即求上式与x轴的交点x1：

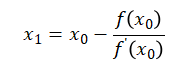
    接着以 斜率为作为斜线，求出与x轴的交点x2，重复上述过程，直到 无限接近于0则停止。最终迭代公式如下：

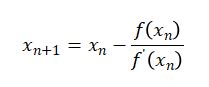
    计算机求解极值时，它会试图首先设置一个初始值，然后不停地迭代，并且达到收敛标准时停止。收敛标准为无限接近于0，在计算机的世界里，即比如小于10的-10次方（即收敛标准），收敛标准到底是10的-10次方，也或者10的-5次方，均由算法决定，其实质原理为接近于0。有时候无论迭代多少次均有可能不收敛，那么算法上默认会有最大迭代次数，如果超出迭代次数还是不收敛，算法也会停止进行下去，只是最终还是不收敛而已。

    上述说明中，初始值由算法决定，而且收敛标准，最大但迭代次数等均是由算法决定。并且求解二元logistic回归的方法上有多种，比如常用的Newton牛顿迭代法，BFGS法（拟牛顿法），lbfgs法等等。

    计算模型的最优解，即模型求解涉及数学模型理论，最优解相关理论知识，计算机最优解求解方法等等，正是基于此种复杂的数学底层原理和最优求解逻辑，带来模型的复杂难懂，并且有时会出现不同的计算软件，比如SPSSAU，R，Stata，SPSS等统计软件，完全相同的数据，但得到不一致的结果。从数学原理上讲，这种概率超低，当前计算机的计算速度惊人，因此数学算法上均会设置很高的收敛标准，足够的迭代次数，每次的迭代增量也足够小，使得模型会收敛且足够精准。但并不排除数据质量很糟糕时，导致迭代不收敛，也或者软件（比如SPSSAU，Stata）会通过使用不同的迭代算法让模型迭代收敛，从而导致具体的内部算法上并不完全一致，得到不同的数据结果，此种情况的概率超低，只会在数据质量足够糟糕，也或者数据量超级大，软件出于计算性能考虑从而自动优化迭代收敛标准或者迭代最大次数等时，才有可能出现。

  • 4、总结

    本文针对二元logistic回归的数学原理进行简要性剖析。在实际数学算法中，还有非常多的模型，比如SPSSAU系统中的多分类logistic回归，有序logistic回归，PLS回归，Lasso回归，非线性回归，二元Probit回归，Poisson回归，Cox回归，条件logit回归，负二项回归，也或者其它涉及算法内部有最优解比如验证性因子分析，路径分析，结构方程模型等多类SPSSAU平台中的算法，均有或多或少的使用到最优求解问题。