与连续性数据或者二分类数据进行Meta分析不同，一般倒方差资料数据只需要提供值和标准误差这两项即可进行Meta分析。但其分析与解读与连续性数据或者二分类数据类似。需要注意的是，一般倒方差Meta分析时提供的是资料值和其对应的标准误差值（非标准差数据）。

• 1、背景

  当前有收集7篇文献均值数据资料如下：包括文献名称（Study）、资料数据如下，提供资料数据及其对应的标准误差值，如下图所示：

  

• 2、理论

  Meta分析时涉及较多的专业名词和分析步骤，具体可见连续性数据或者二分类数据帮助手册。

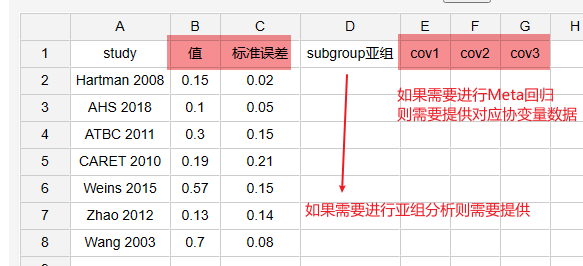
• 3、操作

  本例子中操作截图如下：

  

• 4、SPSSAU输出结果

  Meta模型一共输出7个表格和5个图，说明如下：

  表格/图名称	说明
  基本信息表格	展示Meta模型的基本参数值信息等
  效应量结果	展示核心的模型结果，包括合并效应及其置信区间，以及各研究文献的权重信息等
  森林图	直观展示Meta分析结果
  异质性检验	提供Q检验、tau2、I2、H及其置信区间、H2值等，用于异质性检验
  发表偏倚检验	提供Egger检验和Begg检验
  漏斗图	分析发表偏倚情况
  Trim剪补法	展示基于Trim剪补法对应的‘校正合并效应’结果
  漏斗图（Trim剪补法）	直观展示Trim剪补法后的漏斗图，用于分析发表偏倚情况
  Meta敏感性检验	查看逐一剔除法后的合并效应情况
  森林图（针对敏感性检验）	将敏感性检验结果使用森林图直观展示
  累积Meta效应	展示累积Meta效应的结果汇总
  森林图（针对累积Meta效应）	将累积Meta效应结果使用森林图直观展示

  • 另需要提示的是：

  • 如果有提供‘subgroup亚组’数据，那么系统自动会进行亚组分析，其会改变森林图/效应量表格结果等；

  • 如果有提供协变量数据，并且要求进行Meta回归，那么系统还会提供Meta回归结果，以及Meta回归后的异质性指标信息等。

• 5、文字分析

  

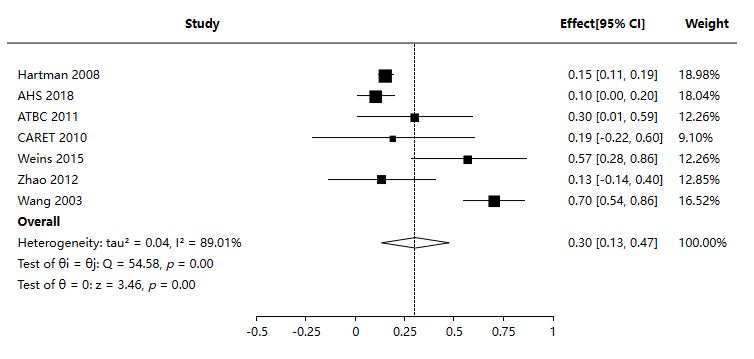
  首先关注异质性问题，从森林图可以看到，I2值为89.01%，意味着有着严重的异质性问题，具体从森林力来看，明显的‘Wang 2003’这个资料数据明显偏离合并效应，意味着其可能带来异质性问题，当然 ‘Weins 2015’这一资料数据也可能是异质性资料，将该2项移除后再次分析，得到森林图如下：

  

  如上图所示，余下5项时进行一般倒方差Meta分析时，I2值为0.00%，此时没有异质性问题，与此同时，图中可以看到‘Hartman 2008’这一资料，其权重值达到82.83%，意味着该资料对于合并效应具有极大的权重影响，具体可查阅原始资料上看，该项的标准误差值为0.02，明显低于其余资料数据的标准误差值，这也正是一般倒方差法IV的原因，标准误差越小时，权重值通常会越大，这在固定效应模型时是绝对成立，在随机效应时，还考虑随机效应误差项，但通常也基本有个通识结论即‘标准误差越小时，其权重会越大’。

  至于其它的SPSSAU输出结果，包括发表偏倚结果，敏感性检验结果和累积Meta效应结果等，具体可见连续性数据或者二分类数据帮助手册，本文档暂不赘述。

• 6、剖析

  Meta分析涉及以下几个关键点，分别如下：

  • Meta分析通常关注三项内容，分别是异质性问题，发表偏倚问题和稳健性问题；异质性问题具有多个检验指标，有时候可能出现不一致结论，建议综合进行决择判断，类似地，发表偏倚也有多种检验和查看方式，通常使用漏斗图查看和分析即可，Meta敏感性检验常用逐一剔除法。