-
Poisson分布是指这样一类数据,其发生频率很低但通常一定会发生而且发生的概率还比较稳定,如果想检验数据是否符合Poisson分布,其共有两种检验方式,一种是通过特征判断;另外一种是通过Poisson检验。在现实研究中,可能更多会通过特征进行判断是否基本符合Poisson分布。如果是使用特征判断,数据需要满足三个特征即:平稳性、独立性和普通性,分别如下:
平稳性:发生频数的大小,只与单位大小有关系(比如1万为单位,或者100万为单位时患癌症人数不同);
-
独立性:发生频数的大小,各个数之间没有影响关系,即频数数值彼此独立没有关联关系;比如前1小时闯红灯的人多了,第2小时闯红灯人数并不会受影响;
普通性:发生频数足够小,即低概率性。
-
特别提示:
-
Poisson分布数据一定是指每单位内的发生频数,比如某个路口每天闯红灯的汽车数量;一年内每万人中丢手机的频数等;
-
SPSSAU提供非加权和非加权两种数据格式,均可进行SPSSAU的Poisson检验。类似下表格中,研究人员观察某路口每天闯红灯的车辆数量,总共观察100天,因而得到100个样本数据,但100个数据最终进行汇总。一列表示‘闯红灯的数量’,另外一列表示有几天出现该种情况。
闯红灯车辆数量 频次 0 3 1 3 2 5 3 8 4 15 5 16 6 15 7 11 8 10 9 8 10 6 -
Poisson检验案例
-
1、背景
某研究人员观察某路口每天闯红灯的车辆数量,总共观察100天,因而得到100个样本数据,最终针对100个数据最终进行汇总如下表。一列表示‘闯红灯的数量’,另外一列表示有几天出现该种情况。此种数据为‘加权格式’数据,如果有100行数据代表100天,只有一列表示该天闯红灯车辆数量,此为‘非加权格式’数据。
闯红灯车辆数量 频次 0 3 1 3 2 5 3 8 4 15 5 16 6 15 7 11 8 10 9 8 10 6 -
2、理论
Poisson数据是指低概率事件的发生频数;这里的低概率是指单位时间内发生的数量非常少,通常仅为个位数,比如每场球赛的进球数量。在进行Poisson检验时,原理上是首先计算数据平均值,接着利用公式去计算出理论频数(如果是Poisson分布应该的发生频数),然后求解理论频数与实际频数的差值,并且进行平方,得到卡方值,最终利用卡方值(并结合自由度df 值)输出p 值,用于判定数据是否为Poisson分布。
在计算各个类别的理论频数之前,首先需要确认好各个类别,SPSSAU默认会对数据进行分类处理,规则如下:
-
如果数据中的最大数字小于20(比如最大为10),则连续性输出0到9共10个数字的实际频数和期望频数,数字最大值10,作为>=10单独作为一个类别计算实际频数和期望频数;
-
如果据中的最大数字超过20(比如最大为30),则连续性输出0到20共21个数字的实际频数和期望频数,并且余下的数字全部处理为>=20归为一类计算实际频数和期望频数。
-
特别提示,检验数据很可能并不是连续的,但输出结果会按照连续数字输出,因而有很多数字的实际频数会为0,但期望频数不为0,这是正常现象且一定需要这样。比如原始数字只包括1,3,5,7;SPSSAU会输出0,1,2,3,4,5,6,>=7共8个类别数据的实际频数和期望频数。
-
-
3、操作
本次数据格式为加权格式数据,操作如下图,‘频数’放入‘权重’框中,如果‘权重’框中不放入项,默认SPSSAU认为是‘非加权数据格式’。
-
4、SPSSAU输出结果
SPSSAU共输出一个表格,包括各类别的实际频数和期望频数,以及卡方值和p 值。如下表:
分析项Poisson分布检验结果 名称 选项 实际频数 期望频数 χ2 值 p 值 闯红灯车辆数量 0.0 3.000 0.385 20.871 0.013* 1.0 3.000 2.140 2.0 5.000 5.949 3.0 8.000 11.025 4.0 15.000 15.325 5.0 16.000 17.042 6.0 15.000 15.792 7.0 11.000 12.543 8.0 10.000 8.718 9.0 8.000 5.386 >=10.0 6.000 5.695 * p <0.05 ** p <0.01 -
5、文字分析
分析项Poisson分布检验结果 名称 选项 实际频数 期望频数 χ2 值 p 值 闯红灯车辆数量 0.0 3.000 0.385 20.871 0.013* 1.0 3.000 2.140 2.0 5.000 5.949 3.0 8.000 11.025 4.0 15.000 15.325 5.0 16.000 17.042 6.0 15.000 15.792 7.0 11.000 12.543 8.0 10.000 8.718 9.0 8.000 5.386 >=10.0 6.000 5.695 * p <0.05 ** p <0.01 针对闯红灯车辆数量进行泊松分布检验,从上表可以看出:闯红灯车辆数量全部均呈现出显著性(χ2=20.871,P < 0.05),意味着拒绝原假设(原假设:数据泊松分布),闯红灯车辆数量全部均不具有泊松分布特质。另外可针对图形进行直观展示实际频数和期望频数的差异性。如下图:
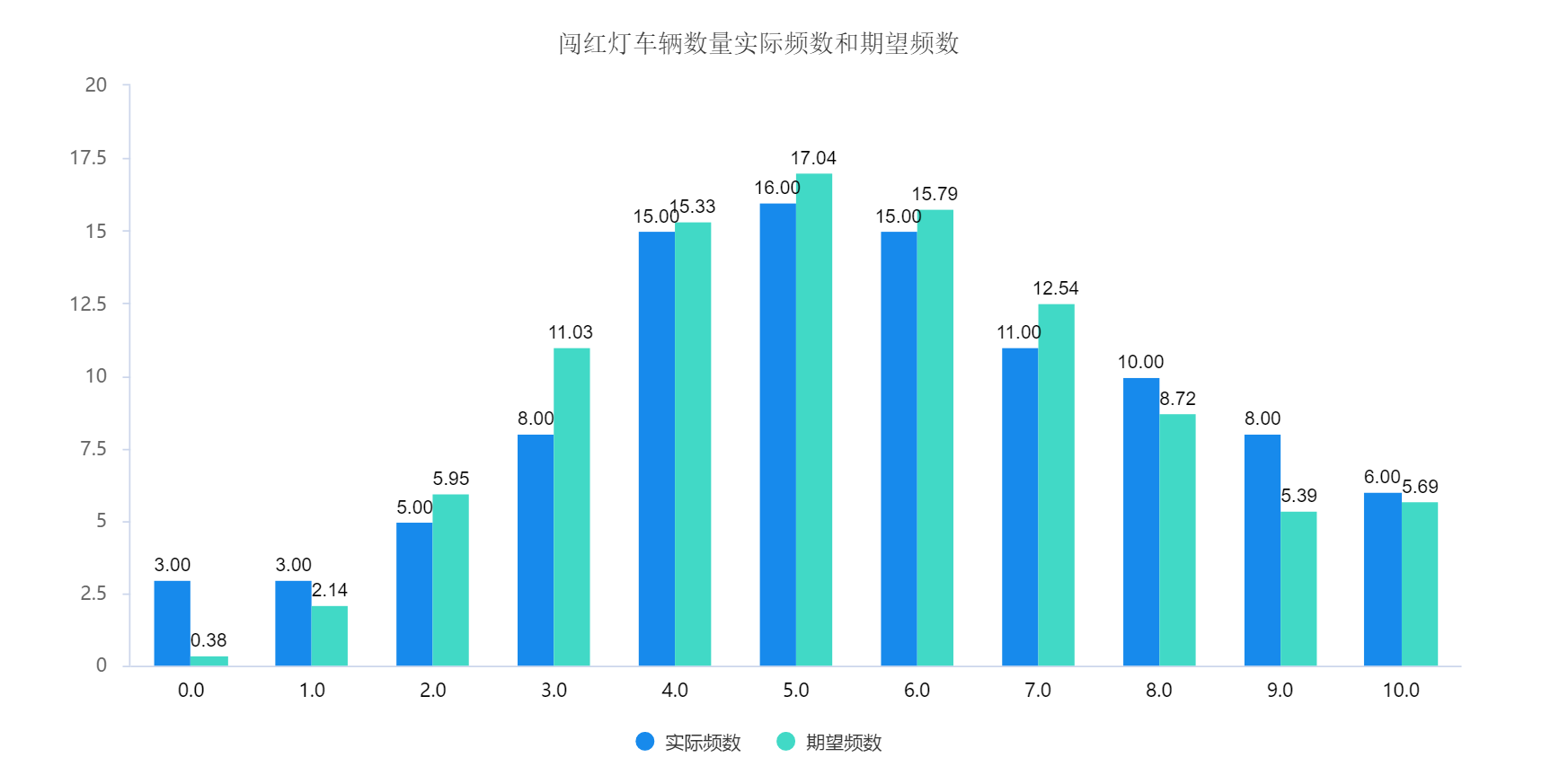
从上图可以看到,发生0次的实际频数为3,但理论频数为0.38次;发生9次的实际频数为8,但理论频数为5.39。另特别提示:从图形上看,实际频数和理论频数差别并不明显,但检验显示无法通过Poisson检验说明不是Poisson分布数据,这种情况较为正常,Poisson检验对于数据分布要求严格,因此稍微一点的差别均为判定为非Poisson分布,建议研究人员可以考虑结合Poisson分布的3个特征进行判定是否为Poisson分布数据。
-
6、剖析
涉及以下几个关键点,分别如下:
-
Poisson分布数据一定是指每单位内的发生频数,比如某个路口每天闯红灯的汽车数量;一年内每万人中丢手机的频数等;
-
Poisson检验共有两种检验方式,一种是通过特征判断;另外一种是通过Poisson检验。在现实研究中,可能更多会通过特征进行判断是否基本符合Poisson分布。
-
SPSSAU提供非加权和非加权两种数据格式,均可进行SPSSAU的Poisson检验。
关于‘加权数据格式’的详细说明参考:https://www.spssau.com/helps/otherdocuments/dataformat.html
-
