-
试想像,你站在路旁收集闯红灯的人群情况。首先,利用秒表和计数器,第一分钟,假设有5个人闯红灯;第二分钟有4个人;而下一分钟有4个人。持续记录下去,你就可以得到一个模型,这便是“泊松分布”的原型。
Poisson模型用于描述单位时间、单位面积或者单位容积内某事件发现的频数分布情况,通常用于描述稀有事件(即小概率)事件发生数的分布;比如1小时内闯红灯的人数;每100万人中患癌症的人数;每100万新生儿童中畸形儿童的人数;每天1万人中丢手机的人数等等。
-
上述例子中明显的一个特点在于:低概率性,以及单位时间(或面积、体积)内的数量;通常情况下,满足以下三个条件时,则称数据满足Poisson分布,三个条件分别是:
-
平稳性:发生频数的大小,只与单位大小有关系(比如1万为单位,或者100万为单位时患癌症人数不同);
-
独立性:发生频数的大小,各个数之间没有影响关系,即频数数值彼此独立没有关联关系;比如前1小时闯红灯的人多了,第2小时闯红灯人数并不会受影响;
-
普通性:发生频数足够小,即低概率性。
如果数据符合这类特征时,而又想研究X对于Y的影响(Y呈现出Poisson分布);此时则需要使用Poisson回归,而不是使用常规的线性回归等。
-
特别强调两点:
-
Y一定是每单位的数据;比如中国每个省的癌症人数,明显的,每个省的人口基数不一致,因此需要加入基数(即每省的人口总数);
-
如果X为定类数据,则需要进行虚拟变量设置。
-
-
SPSSAU分析结果表格示例如下:
模型似然比检验汇总 似然比卡方值 df p AIC 值 BIC 值 1041.929 2 0.000 121.649 122.557 -
Poisson回归分析结果汇总 项 回归系数 标准误 z 值 p 值 OR值 OR值95% CI(LL) OR值95% CI(UL) 性别_女 -0.035 0.189 -0.187 0.852 0.965 0.666 1.399 年龄 0.643 0.025 25.972 0.000 1.902 1.812 1.997 截距 -9.952 0.159 -62.447 0.000 0.000 0.000 0.000 因变量Y: 皮肤癌人数 McFadden R 方: 0.900
Poisson 回归案例
-
1、背景
当前有一份数据是用来研究影响患皮肤癌的影响因素,共有两个研究因素,分别是性别和年龄;以及被影响项为‘是否皮肤肺癌’。由于Y为‘是否皮肤肺癌’,而且明显的,‘是否皮肤肺癌’这个数据满足平稳性、独立性和普通性这三个特征;因而使用Poisson回归进行研究。
研究数据来源共从10个城市进行抽样获取所得,由于每个城市的基数并不一致,因此数据还带有10个城市的人口基数这一数据。原始数据如下:
城市编号 性别 年龄 皮肤癌人数 人口基数 1 2 1 1 172675 2 2 2 16 123065 3 2 3 30 96216 4 2 4 71 92051 5 2 5 102 72159 6 2 6 130 54772 7 2 7 133 32185 8 2 8 40 8328 9 1 1 4 181343 10 1 2 38 148207 性别中,1代表男、2代表女;年龄的数字代表年龄组别,数字越大代表年龄越大。
-
2、理论
Poisson回归研究X对于Y的影响关系,其中X通常为定量数据(如果X为定类数据,一般需要做虚拟(哑)变量设置),Y为Poisson分布数据。分析共分为两步:第一步是对模型整体情况进行检验;第二步具体分析X对于Y的影响情况,首先分析p 值,如果此值小于0.05,说明具有影响关系,接着再具体研究影响关系情况即可,比如是正向影响还是负向影响关系等;除此之外,还可以写出Poisson回归分析的模型构建公式,以及模型的预测准确率情况等。
-
特别提示
-
一定注意,Y一定要符合Poisson分布特征;
-
Poisson分布是指单位时间/面积/体积内的发生数,因而如果基数不一致时,spssau分析时,一定要放入基数这个数据。
-
如果X为定类数据,通常情况下需要将X进行虚拟(哑)变量设置【SPSSAU中生成变量功能中有,比如本研究的性别】。
-
-
3、操作
本例子中研究X对于Y的差异;X分别为性别和年龄【其中性别为定类数据,因而做虚拟变量处理后,将性别_女放入模型,男性作为对照】,Y为‘是否皮肤肺癌’。并且带着基数,因而放置如下:
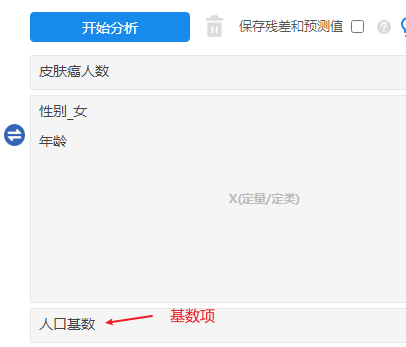
-
4、SPSSAU输出结果
模型似然比检验结果 似然比卡方值 df p AIC 值 BIC 值 1041.929 2 0.000 121.649 122.557 第一个表格用于模型检验,模型检验的原定假设为“是否放入X模型质量均一样”,此处放入2个X分别是性别_女,年龄。而且p 值为0.000 <0.05,意味着放入2个自变量后,模型质量有明显的提升,因而拒绝原定假设,本次模型构建有意义。卡方值和df 值均为中间过程值可忽略。 以及AIC和BIC这两个指标值,可用于多个模型对比(AIC和BIC越小越好),当前放入2个自变量可记录下AIC和BIC 值,如果多放一个自变量(即3个时),AIC和BIC 值有着明显的下降,则可以选择3个自变量时的模型作为最终模型。
-
Poisson回归分析结果汇总 项 回归系数 标准误 z 值 p 值 OR值 OR值95% CI(LL) OR值95% CI(UL) 性别_女 -0.035 0.189 -0.187 0.852 0.965 0.666 1.399 年龄 0.643 0.025 25.972 0.000 1.902 1.812 1.997 截距 -9.952 0.159 -62.447 0.000 0.000 0.000 0.000 因变量Y: 皮肤癌人数 McFadden R 方: 0.900 第二个表格用于研究X对于Y的影响关系情况,表格中有意义的指标信息包括:p 值,回归系数和R Pseudo R 2。其它指标包括标准误,z 值,95% CI值意义相对较小。
-
5、文字分析
模型似然比检验汇总 似然比卡方值 df p AIC 值 BIC 值 1041.929 2 0.000 121.649 122.557 进行Poisson回归模型构建时,首先对于模型检验进行分析,模型假假设为是否放入自变量时质量均一致。从上表可知,p 值为0.000 <0.05,意味着本次模型构建有意义。
Poisson回归分析结果汇总 项 回归系数 标准误 z 值 p 值 OR值 OR值95% CI(LL) OR值95% CI(UL) 性别_女 -0.035 0.189 -0.187 0.852 0.965 0.666 1.399 年龄 0.643 0.025 25.972 0.000 1.902 1.812 1.997 截距 -9.952 0.159 -62.447 0.000 0.000 0.000 0.000 因变量Y: 皮肤癌人数 McFadden R 方: 0.900 从上表可知,将性别_女, 年龄共2项为自变量,而将皮肤癌人数作为因变量进行Poisson回归分析,从上表可以看出,模型伪R 2值(Pseudo R 2)为0. 900,意味着性别, 性别和年龄可以解释皮肤癌患病的90.0%变化原因。从上表可知:模型公式为:log(u)=log(人口基数) -9.952-0.035*性别_女 + 0.643*年龄(其中u代表期望均数)。最终具体分析可知:
-
性别_女的回归系数值为-0.035,但是并没有呈现出显著性(p =0.852>0.05),意味着相对于男性来讲,女性患皮肤癌情况并没有明显的差异,也即说明性别对于患皮肤癌并不会产生影响。
-
年龄的回归系数值为0.643,并且呈现出0.01水平的显著性(p =0.000 <0.01),意味着年龄会对患皮肤癌产生显著的正向影响关系。以及优势比(OR值)为1.902,意味着年龄增加一个单位时,患皮肤症的的概率增加1.902倍。
-
总结分析可知:年龄会对皮肤癌人数产生显著的正向影响关系。但是性别并不会对皮肤癌人数产生影响关系。
6、剖析
Poisson回归分析涉及以下几个关键点,分别如下:
-
Poisson分布是指单位时间/面积/体积内的发生数,因而如果基数不一致时,spssau分析时,一定要放入基数这个数据。
-
如果X是定类数据,此时需要对X进行虚拟(哑)变量设置【虚拟变量设置参考: https://www.spssau.com/helps/otherdocuments/dummy.html 】。
关于‘加权数据格式’的详细说明参考:https://www.spssau.com/helps/otherdocuments/dataformat.html
疑难解惑
-
O检验的意义?
-
Poisson回归要求数据等离散(即平均值和方差一致),O检验用于检测数据是否等离散。如果O值绝对值大于1.96(此时p 值小于0.05),则说明数据过离散,此时可考虑使用负二项回归进行研究。如果O值绝对值小于1.96 (此时p 值大于0.05),则说明数据等离散,此时数据适合使用Poisson回归
-
SPSSAU的Poisson回归时基数是什么意思?
-
泊松回归中基数是基于某个数字的意思,比如有30个省每年癌症患者人数,但是癌症患者人数是基于某省所有人数时才有对比意义。
-
泊松检验没有输出结果?
-
SPSSAU中,如果‘发生次数’>100则不输出该项的分析结果。默认情况下泊松分布数据具有发生次数很低但会稳定发生等特点,如果平均的发生次数即lambda值大于20,此时数据不应该是泊检分布数据,而应该考虑其正态性特质。
