正交实验

正交实验（正交设计，也称田口设计）是研究多因素多水平的一种设计方法。比如说现在想研究3个因素（分别称之为A,B,C），A因素有3个水平，B因素有3个水平，C因素有3个水平。那么如果是做实验，如果想cover所有情况，那么实验次数为：3*3*3=27种组合，即需要做27次不同的实验才行。

但在实际研究时，出于时间，成本费用等考虑，不可能做27次实验，那么是否可以只做部分有代表性的实验去cover各类情况呢？正交实验正是这种方法，其仅选出部分具有代表性的实验组合，并且这些代表性的实验组合具有分散、整齐可比等特点，从而可以科学有效的代表所有实验组合。正交实验可以极大地简化实验次数，从而提升实验效率和减少实验成本。

同时SPSSAU系统中可自主选择正交表，包括下拉选择常用正交表，以及输入正交表ID查看更多正交表。

正交实验完成后，通常需要进行方差分析（也称极差分析），比如本例子中有3个因素，则需要进行三因素方差分析（也或者如果有协变量时，需要使用协方差分析）；一般情况下，实验的因素为两个或者三个即可，如果超过三个，则需要使用多因素方差分析。这些研究方法均可以在SPSSAU进阶方法里面找到。

正交实验案例

  • 1、背景

    当前想研究三种因素对于弹簧质量的影响；三种因素分别是温度，保温时间和工件重量。因素和水平数据如下表：

    水平 因素A：温度（度） 因素B：保温时间（分） 因素C：工件重量（Kg）
    1 460 3 6
    2 480 4 8
    3 500 5 10

    如果不进行正交实验，那么实验组合次数为3*3*3=27种组合；显然实验次数太多，因此使用SPSSAU的正交实验方法进行操作，得出部分有代表性的实验组合。

  • 2、理论

    正交实验是一种减少实验组合次数的实验设计方法，其可以通过选择部分有代表性的实验组合，去表示所有实验组合，从而提升实验效率并且减少实验成本的一种方法。

    • 特别提示

    • 在完成实验记录好数据后，后续一般需要使用方差分析（也称极差分析）去研究实验因素对于研究因素的影响情况，方差分析可通过SPSSAU的进阶方法找到；

    • 同时可自主选择正交表，包括下拉选择常用正交表，以及输入正交表ID查看更多正交表。

  • 3、操作

    本例子有3个因素，3个因素分别均为3个水平，因此进行操作如下：

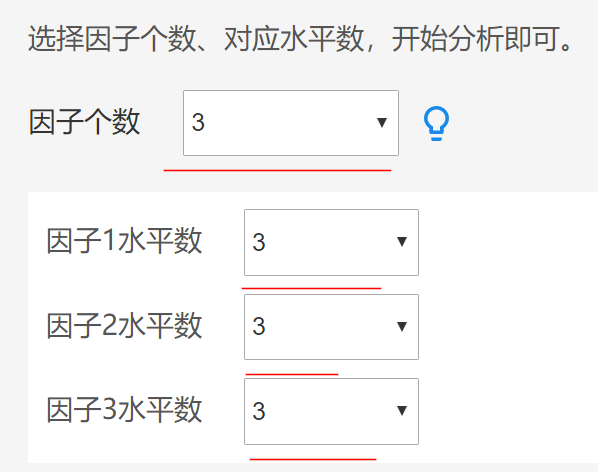
    首先选择因素（也称因子）个数，然后分别录入每个因素（因子）的水平个数情况，点击“开始分析”即可。

    同时,SPSSAU提供自选正交表，比如本次中3个水平的因子个数为3；可以考虑选择L9.3.4(共进行9次实验,3个水平的因子个数为4)。当然也可以自己输入正交表ID查询。SPSSAU输入正交表ID的格式举例说明如下：

  • 4、SPSSAU输出结果

    SPSSAU仅输出正交设计表，即最终的实验组合汇总表格，如下：

    正交设计表
    编号 因子1 因子2 因子3
    1 1 1 1
    2 2 2 1
    3 3 3 1
    4 3 2 2
    5 2 1 2
    6 1 3 2
    7 1 2 3
    8 2 3 3
    9 3 1 3

  • 5、文字分析

    正交设计表
    编号 因子1 因子2 因子3
    1 1 1 1
    2 2 2 1
    3 3 3 1
    4 3 2 2
    5 2 1 2
    6 1 3 2
    7 1 2 3
    8 2 3 3
    9 3 1 3

    总共3个因素，并且每个因素均为3个水平。

    • 特别提示

    • 上表格中编号代表实验组合的编号，“因子1”，“因子2”，“因子3”等均为默认的名称，即本案例中的温度，保温时间和工件重量，里面的数字1，2，3代表水平的编号，此编号代表的意义由研究者决定即可。比如本案例中“因子1”即温度时，数字1表示460度，数字2表示480度，数字3表示500度。

  • 6、剖析

    涉及以下几个关键点，分别如下：

    • 在完成实验记录好数据后，后续一般需要使用方差分析（也称极差分析）去研究实验因素对于研究因素的影响情况，方差分析可通过SPSSAU的进阶方法找到。

    • SPSSAU提供163个正交表（水平数量全部均小于10），用户可下载下述链接查看，并且输出正交表ID得到具体正交表；链接如下：https://pubimage.spssau.com/SPSSAU%E6%AD%A3%E4%BA%A4%E8%A1%A8%E6%89%8B%E5%86%8C2020%E7%89%88.xlsx

    • SPSSAU输入正交表ID的格式举例说明如下：

    • L8.2.4.4.1：L8表示需要8次实验，2水平的因子有4个，4水平的因子为1个；各项以英文句号隔开。

    • L12.2.2.6.1：L12表示需要12次实验，2水平的因子有6个，6水平的因子为1个；各项以英文句号隔开。

    • 如果自主选择正交表，可能还需要使用‘拟水平法’，‘组合法’，‘并列法’等对正交表进行处理，最终得到自己需要的正交表，建议查看视频内容。

    • 有可能得到正交表完成实验数据后，进行后续方差分析，却无法进行交互作用的研究，此类情况需要提前预防，建议查看视频内容。

疑难解惑

  • 正交表和文献结果不一样？

  • 正交表有很多，同样的因子数量和水平数，生成得到的正交表均有可能不同。

  • 正交实验数据无法进行方差分析（比如双因素/三因素/多因素等）？

  • 如果进行正交设计并且进行实验得到数据后，进一步进行方差分析。可能需要考虑自由度问题。比如得到L9.3.4的正交表。

  • 到L9.3.4的正交表共9次实验，那么该正交表的自由度为实验次数 - 1 = 9 – 1 = 8。

  • 4个因子每因子3水平，如果要进行四因素方差分析（且不考虑二阶作用时），最少要求的自由度=（每因子水平 – 1）的累和 +1 =（3-1）+（3-1）+（3-1）+（3-1）+ 1 = 9。

  • 方差分析（且不考虑二阶作用时）最少要求9个自由度，也即说明实验次数最少为9+1=10次实验才可以。但当前L9.3.4正交表仅8个自由度，因此该正交表不能进行四因素方差分析。

  • 如果是进行方差分析（且考虑二阶作用时），方差分析要求的自由度会多很多【最小自由度计算公式为：（每个因子水平数-1）的累和 + 两两因子自由度即（因子水平数-1）的乘积的累积 +1 】。比如4因子每个为3水平，此时进行四因素方差分析（且考虑二阶作用时），方差分析的自由度要求至少是：【（3-1）+（3-1）+（3-1）+（3-1）+ （3-1）*（3-1）+（3-1）*（3-1）+（3-1）*（3-1）+（3-1）*（3-1）+（3-1）*（3-1）+（3-1）*（3-1）+ 1 =33】，即最少要求33个自由度，那么实验次数最少需要为34次。

  • 拟水平法，组合法，并列法分别是什么意思？

  • 由SPSSAU系统自动提供正交表后，很可能并不满足完全满足预期，因此需要进行以下处理。

  • 如果有超出的多余因子，直接删除即可；

  • 如果某因子的水平数比预期多，比如生成正交表的因子1有5个水平，但只需要4个水平；那么此时把多出的数字5（第5个水平），直接用其它4个水平中任意一个或多个替换填补即可。此种处理叫‘拟水平法’。‘拟水平法’在正交表改造处理中非常常见，但‘拟水平法’后，可能就不再具有正交表特性，这是非常正常的；

  • ‘组合法’：比如考虑2水平，4水平，8水平；并不需要一定使用2.1.4.1.8.1；而是使用比如L12.2.11（因为2水平有16个，可拆分成：2，2*2，2*2*2，共用掉6个因子，都还余5个因子没有使用直接删除即可），组合法是一种正交表获取的技巧操作法，该操作法是在正交表生成前自行处理和选择，以及‘组合法’对于正交性没有任何影响，只是一种手工选择正交表的技巧做法；

  • ‘并列法’： 指把两列或多列，合并成1列，比如有两个因子其中1个为2水平另1个为3水平；把两个因子合并变成2*3=6水平；‘并列法’是自主手工选择正交表的一种技巧式做法，‘并列法’后正交性还在。

  • 为什么正交表的因子/因素数量（列数）与我要求(预期)不一致？

  • SPSSAU默认找到最接近的标准正交表，比如预期找3个因素的正交表，3个因素分别有3，4或5个水平。

  • SPSSAU默认会找到最接近的标准正交表L25.5.6，即5水平的因子共6个，意味着有6列（而不是3列）。

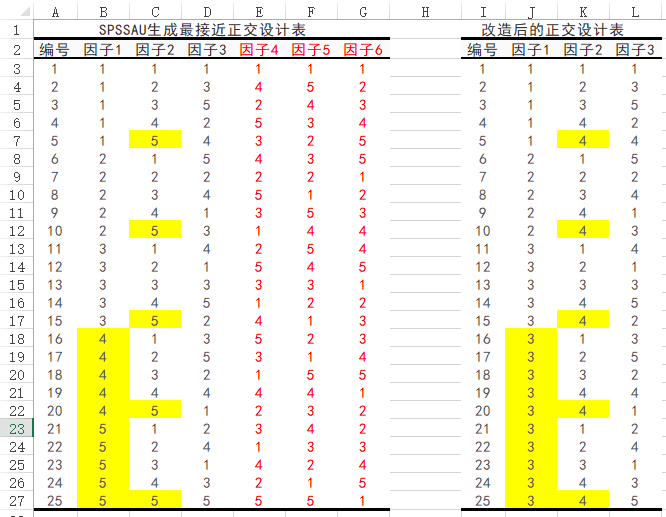
  • 此时就需要结合组合法（删除掉任意3列，余下3列），余下3列均是5个水平，但当前需要3，4，5水平）。接着还需要结合拟水平法，将多出的1个水平或2个水平，用其它任意的水平进行填补替换即可，拟水平法一般需要结合专业知识进行，其相当于是对正交表进行改造。具体如下图说明：

  • SPSSAU得到6列，但只需要3列，删除掉最后3个因子（即红色的3个因子），余下因子1，因子2和因子3。因子1有5个水平（但只需要3个水平），将水平4和水平5填补替换成水平3（当然也可以1或2或混合1/2/3均可）；因子2有5个水平（但只需要4个水平），将水平5填补替换成水平4（当然也可以1或2或3或混合1/2/3/4均可）。

  • 为什么做不了多因素方差分析？

  • 正交表和多因素方差分析，二者完全独立，因此有时候会出现正交表出来了但无法进行多因素方差分析，原因在于实验次数过少自由度不足导致无法进行多因素方差分析。比如正交表L9.3.4，4因子3水平的正交表。如果需要进行多因素方差分析，至少需要的自由度数量需要大于：4*(3-1)+1=9，那么最少需要10次实验才够4因子3水平的正交表进行多因素方差分析。解决办法有两个，一是选择实验次数更高的正交表；二是自己多做最少一次实验（且实验组合不能与正交表中已有的组合相同）。

  • 提示“选择使用更多实验次数的正交表”？

  • 如果提示‘需要自选实验次数更多的正交表’，意味着该正交表确实已经生成，但无法进行后续的多因素方差分析，原因在于自由度不够。解决办法有两个，一是选择实验次数更高的正交表；二是自己多做最少一次实验（且实验组合不能与正交表中已有的组合相同）。