如果研究X对于Y的影响,Y是计数资料(比如专利数量,肺癌人数,抢劫犯罪次数等,非正态分布数据),一般可以使用Poisson回归进行研究。很多计数资料数据均满足Poisson分布,但Poisson分布对数据要求较为严格,包括数据平稳性,独立性,普通性,并且Poisson分布的数据应满足平均值等于方差,即等离散性。
实际研究中,很多数据为过离散(即不是等离散),比如研究传染病人数,传染病人数明显具有一些空间聚焦现象;以及专利数量,很可能企业之间存在着某种空间意义上的竞争,导致数据具有聚焦现象,诸如此类数据其并不满足Poisson分布的独立性原则。此类数据通常情况下方差会明显的大于平均值,属于过离散数据,此种数据在进行Poisson回归时会导致模型参数估计值的标准误偏小(参数检验的假阳性,不应该显著的项但出现显著)。
因而,如果计数资料不适合Poisson分布时,尤其是数据过离散时,此时使用负二项回归分析更合适。关于数据过离散的检验,SPSSAU在Poisson回归时默认有提供O检验,用于检验数据是否存在过离散现象。
Poisson回归时因变量Y的方差为λ,在负二项回归模型时方差等于λ(1+kλ),当k值趋这于0时,负二项回归就完全等于Poisson回归。k>0则说明具有过离散现象。过离散是负二项回归模型存在的关键原因,几乎所有的负二项回归模型均是基于Poisson回归出现过离散现象时即会使用。
-
-
特别提示:
-
在SPSSAU中,可通过O检验,alpha值的检验,以及平均值和方差的大小对比,综合判断是否存在过离散现象。
-
过离散现象可通过O检验(在Poisson回归分析时SPSSAU默认有提供)
-
过离散现象的检验可针对alpha值进行检验,在负二项回归时默认输出,如果alpha值显著不为0(对应的P值小于0.05),则说明使用负二项回归较为合理,反之则说明可能使用Poisson回归较优。
-
如果说描述分析时发现平均值与方差值有着较大的差异,则说明负二项回归较合理,如果说平均值与方差值基本相等,说明可能使用Poisson回归较为合适。
-
负二项回归案例
-
1、背景
当前有一项针对专利数量的影响关系研究,研究政府对于企业的支持力度,是否一线城市,对于企业专利数量的影响情况。共收集10个城市的数据,如下:
X1是否一线城市 X2政府扶持力度 Y专利数量 Weight企业数量 0 8 40 8328 1 7 133 32185 1 6 130 54772 1 5 102 72159 0 4 71 92051 0 3 30 96216 0 2 16 123065 0 2 38 148207 0 1 1 172675 0 1 4 181343 -
X1是否一线城市:数字1表示为一线城市,数字0表示非一线城市;
-
X2政府扶持力度:数字越大表示对于企业申请专利时的扶持力度越大;
-
Y专利数量:数字表示某城市调研所有企业申请成功的专利数量;
-
Weight企业数量:数字表示某城市调研的企业数量。
-
-
2、理论
如果说因变量Y为计数数据,一般可使用Poisson回归,但是Poisson回归要求数据满足等离散现象(平均值与方差相等),如果说数据具有一定的聚焦性,此时很可能就会产生过离散现象,即数据平均值与方差明显不相等。此时使用负二项回归更为科学。关于过离散的检验有很多检验方法,在SPSSAU系统中可有三种方式进行综合判断,分别如下:
-
如果说描述分析时发现平均值与方差值有着较大的差异,则说明负二项回归较合理,如果说平均值与方差值基本相等,说明可能使用Poisson回归较为合适。
-
过离散现象可通过O检验(在Poisson回归分析时SPSSAU默认有提供)
-
过离散现象的检验可针对alpha值进行检验,在负二项回归时默认输出,如果alpha值显著不为0(对应的P值小于0.05),则说明使用负二项回归较为合理,反之则说明可能使用Poisson回归较优。
-
-
3、操作
本例子中专利数量是基于‘Weight企业数量’,因此‘基数Eposure【可选】’框中应该放入‘Weight企业数量’这项,如下图:
-
4、SPSSAU输出结果
SPSSAU共输出两个表格,分别是“负二项回归模型似然比检验”,“负二项回归分析结果汇总”。 “负二项回归模型似然比检验”是针对整个模型的检验,如果说模型p值小于0.05,意味着放入自变量更优,即模型有意义。“负二项回归分析结果汇总”是回归结果的具体结果。
-
5、文字分析

在进行负二项回归之前,专利数量的平均值是56.500,方差是2480.944,明显平均值与方差不相等,存在过离散现象。而且使用SPSSAU的Poisson回归时,对其提供的O检验发现,O值明显大于1.96(p=0.000 <0.05),拒绝等离散假定,说明数据存在明显的过离散现象,因此使用负二项回归较为适合。

模型似然比检验用于对整体模型有效性进行分析。
-
第一:首先对p值进行分析,如果该值小于0.05,则说明模型有效;反之则说明模型无效;
-
第二:AIC值和BIC值可用于多次分析模型时的对比;此两个值越低越好;如果多次进行分析,对比该两个值的变化情况,综合说明模型构建的优化过程;
-
首先对模型整体有效性进行分析,模型检验的原定假设为:是否放入自变量(X1是否一线城市, X2政府扶持力度)两种情况时模型质量均一样;检验p值为0.000小于0.05,因而说明拒绝原定假设,即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。
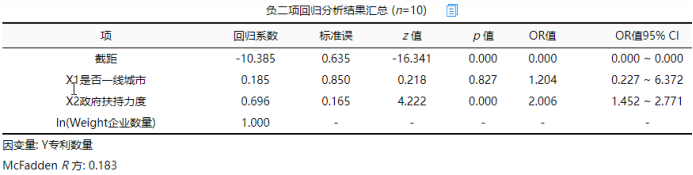
从上表可知,将X1是否一线城市, X2政府扶持力度共2项为自变量,而将Y专利数量作为因变量进行负二项回归分析,从上表可以看出,模型公式为:Log(Y)=-10.385 + 0.185*X1是否一线城市 + 0.696*X2政府扶持力度 + ln(Weight企业数量)。模型的伪R 方值(McFadden R 方)为0.183,说明研究模型可以解决专利数量18.3%的原因。具体分析可知:
X1是否一线城市的回归系数值为0.185,但是并没有呈现出显著性(z =0.218,p =0.827>0.05),意味着X1是否一线城市并不会对Y专利数量产生影响关系,即城市类别与专利数量无明显关系。X2政府扶持力度的回归系数值为0.696,并且呈现出0.01水平的显著性(z =4.222,p =0.000<0.01),意味着X2政府扶持力度会对Y专利数量产生显著的正向影响关系,以及优势比(OR值, exp(b)值)为2.006,意味着X2政府扶持力度增加一个单位时,Y专利数量的增加幅度为2.006倍。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
在SPSSAU系统中可有三种方式进行综合判断,分别如下:
-
如果说描述分析时发现平均值与方差值有着较大的差异,则说明负二项回归较合理,如果说平均值与方差值基本相等,说明可能使用Poisson回归较为合适。
-
过离散现象可通过O检验(在Poisson回归分析时SPSSAU默认有提供)
-
过离散现象的检验可针对alpha值进行检验,在负二项回归时默认输出,如果alpha值显著不为0(对应的p值小于0.05),则说明使用负二项回归较为合理,反之则说明可能使用Poisson回归较优。
-
疑难解惑
-
O检验在哪里?
-
Poisson回归时SPSSAU默认提供O检验,O检验用于检测数据是否等离散。如果O值绝对值大于1.96(此时p 值小于0.05),则说明数据过离散,此时可考虑使用负二项回归。如果O值绝对值小于1.96 (此时p 值大于0.05),则说明数据等离散,此时数据适合使用Poisson回归。
-
O检验、平均值和方差、alpha值检验出现矛盾?
-
O检验和alpha值是否为O检验,目的均在于对“过离散”进行检验,平均值和方差的直观查看也是一种方式。有时候会出现比如平均值和方差看上去有非常大的差异,但alpha值均没有呈现出显著性(即没有拒绝alpha值为0),此时建议综合进行判断,通常情况下使用负二项回归更“保险”,因为负二项回归对模型的假定没有Poisson回归那么严格。
-
R 方值很低怎么办?
-
R 方值的意思在于模型拟合程度,即X对于Y的解释力度情况。通常情况下R 方值并不太高是正常的,因为不可能把可能对Y产生影响的X都全部研究。通常建议查看影响关系情况即可,即查看p 值分析情况,不用过度在意R 方值大小。
-
SPSSAU负二项回归时O检验的意义是什么?
-
SPSSAU进行负二项回归时,一般需要满足过离散性,离散性检验有多种,SPSSAU默认提供O检验。如果说通过O检验,如果O值绝对值大于1.96(此时p 值小于0.05),则说明数据过离散,此时说明适合使用负二项回归进行研究。如果O值绝对值小于1.96 (此时p 值大于0.05),则说明数据等离散,此时建议使用Poisson回归。
-
SPSSAU的负二项回归时基数是什么意思?
-
负二项回归的基数是基于某个数字的意思,比如有30个省每年癌症患者人数,但是癌症患者人数是基于某省所有人数时才有对比意义。
-
OR值和IRR值?
-
SPSSAU中OR值的计算公式为exp(b),即自然对数的回归系数次方。IRR值即发生率比值,其为经济计量研究中使用的称呼,其计算公式也为exp(b),与OR值完全一致。即IRR值就为OR值。
