均值z 检验

•  分析方法视频解读：B站优酷

如果希望对比平均值的差异性，包括一组数据与某数字的差异性；也或者是两组数据的平均值差异性；此时可使用t 检验或者z 检验，二者区别在于小样本只能使用t 检验；而大样本时(样本量大于30)使用z 检验（也称U检验）或者t 检验均可。如果是大样本（N >30），z 检验和t 检验可以互换使用。

z 检验也分为两种类型，分别是单样本z 检验，即研究一组数据与某数字的差异性；两样本z 检验，即研究两组数据之间的差异关系。

• 1、背景

  收集某地区100名，20岁男子身高数据，平均身高为168cm，标准差为14cm。资料显示该地区10年前平均身高为165cm，分析当前身高是否明显比10年前更高？

  本案例样本数量为100>30，属于大样本，因而可使用z 检验，原假设是：168cm>165cm，只对比一个数字的差异性；此为单样本z 检验。

  收集某A地区100名，20岁男子身高数据，平均身高为168cm，标准差为14cm。收集B地区200名，20岁男子身高数据，平均身高为170cm，标准差为13cm。分析A地区和B地区身高是否有明显差异？

  本案例两组数据样本数量均大于30，属于大样本，因而可使用z 检验，原假设是：168cm=170cm（差值对比为0），只对两组数据的均值差异；此为两样本z 检验。

• 2、理论

  无论是单样本z 检验，还是两样本z 检验，均是对比数据的差异性，区别在于单样本z 检验和一个已知数字进行对比；两样本z 检验进行两组数据的均值差异对比。进行z 检验时，需要输入三项数据，分别是平均值，标准差和样本量。

  除此之外，z 检验还需要知道以下三个术语，分别是差值对比、置信水平和假设检验。

  • 对比均值(差值对比)：两样本z 检验时，对比数字是指两组数据均值差，与某个数字进行对比，通常情况下是0（即两组数据平均值差值，与数字0进行对比PK）。

  • 置信水平：指在多大程度上对假设有把握，通常为95%，可选为99%和90%。

  • 假设检验：原假设是等于，小于，还是大于，通常情况下等于（即直接对比是否相等，即是否有差异）。

• 3、操作

  本次涉及两个例子，分别操作如下：

  

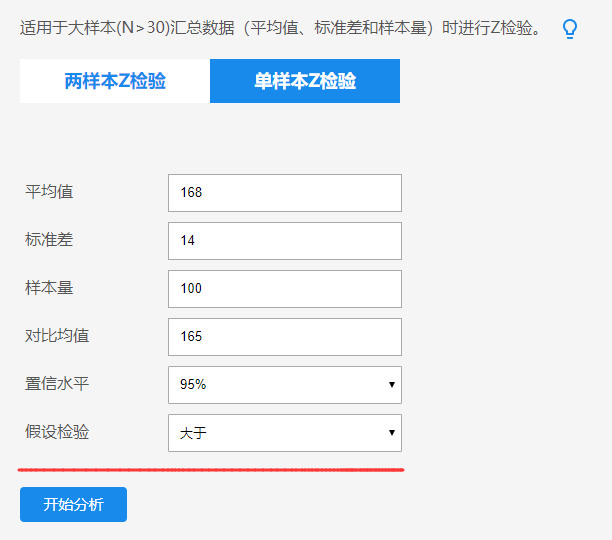
  上图显示收集数据与165cm进行对比，因此对比均值为165；默认置信水平为95%，即对此次分析结论有95%的把握；以及研究假设为均值168cm是否明显大于165cm，因而假设检验选择为大于。

  

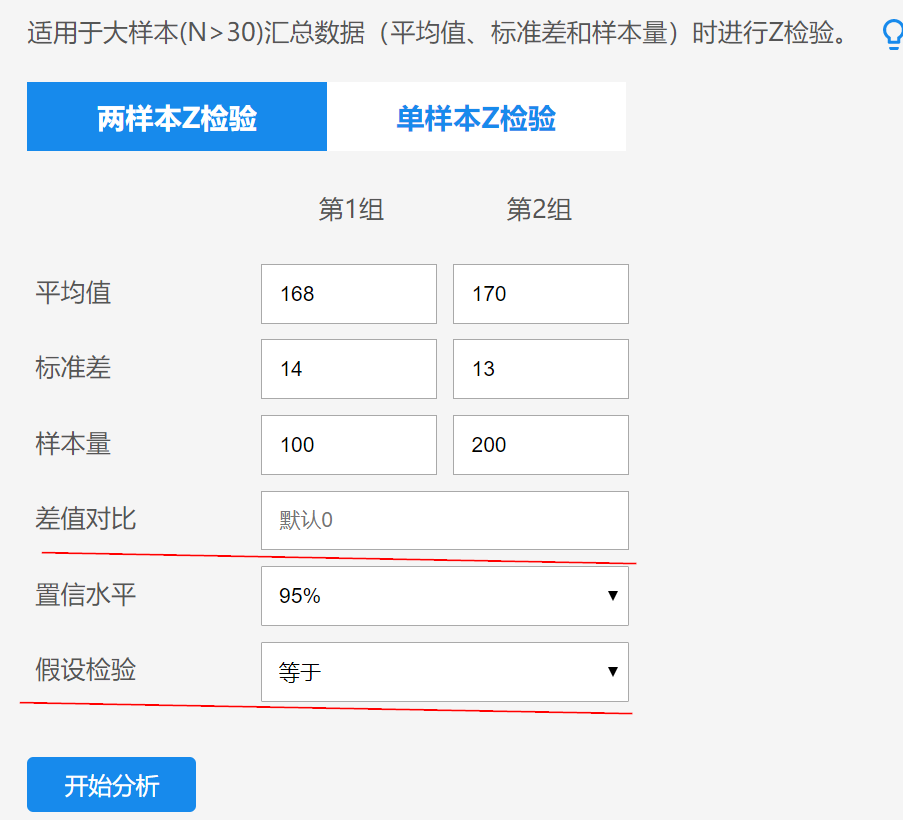
  上图显示两组身高进行对比，研究的是两组身高平均值相等（即差值与数字0进行对比），因此差值对比处输入数字0；【如果是研究A地区身高，明显低出B地区身高2cm，那么差值对比值则输入2】；默认置信水平为95%，即对此次分析结论有95%的把握；以及研究假设为均值168cm是否明显等于170cm，因而假设检验选择为等于。

• 4、SPSSAU输出结果

  针对单样本z 检验，SPSSAU共输出两个表格，分别是区间估计和假设检验【置信区间仅列出区间估计意义较小，假设检验针对原假设进行验证】，分别如下：

  单样本z 检验置信区间
  项	样本量	平均值	标准差	标准误	95% CI(LL)	95% CI(UL)
  值	100	168.000	14.000	1.400	165.256	170.744

  

  本次收集样本为100个20岁男子身高，平均值为168cm，标准差为14cm，分析显示身高的95% CI为：165.256cm~170.744cm。即有95%的把握身高应该介于165.256cm到170.744cm之间。

  单样本z 检验假设检验
  项	样本量	平均值	检验均值	假设	z	p	检验结论
  值	100	168.000	165.000	168.000>165.000	2.143	0.984	假设成立

  

  本次研究假设为100名20岁男子身高168cm，是否明显高于165cm，因此原假设为168cm>165cm，检验显示在0.05水平上接受原假设（z =2.143，p =0.984>0.05），即意味着当前168cm的身高明显比10年前165cm身高有明显的提升，这一说法无法被论证错误，即说明当前168cm身高明显比10年前165cm要高。

  针对两样本z 检验，SPSSAU共输出两个表格，分别是区间估计和假设检验【置信区间仅列出区间估计意义较小，假设检验针对原假设进行验证】，分别如下：

  两样本z 检验差值置信区间
  项	第一组(n=100)		第二组(n=200)		均值差值	差值标准误	95% CI(LL)	95% CI(UL)
  	平均值	标准差	平均值	标准差
  值	168.000	14.000	170.000	13.000	-2.000	1.675	-5.283	1.283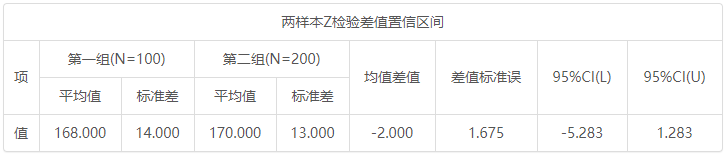

  

  本次收集A地区和B地区20岁男子身高数据，A地区为168cm，B地区为170cm，A地区与B地区的身高差值为-2cm，而且差值95% CI为：-5.283cm~1.283cm。即有95%的把握两个地区身高差值，应该介于-5.283cm到1.283cm之间。

  两样本z 检验差值假设检验
  项	均值差值	差值检验值	假设	z	p	检验结论
  值	-2.000	0.000	-2.000=0.000	-1.194	0.232	假设成立

  

  本次研究假设为A地区168cm的男子身高，是否与B地区170cm男子身高，有没有明显的差异性。上表格显示，从数字上看，A地区身高会低于B地区身高2cm，检验2cm是否与数字0相等。检验显示在0.05水平上接受原假设（z =-1.194，p =0.232 >0.05），即意味着2cm的身高差值，与没有身高差异，二者之间无统计学意义；也即说明此2cm的身高差异并不明显，也即验证说明A地区和B地区男子身高并没有非常明显的差异性。

• 5、文字分析

• 6、剖析

  涉及以下几个关键点，分别如下：

  • z 检验涉及以下三个术语，分别是差值对比、置信水平和假设检验。

  • 对比均值(差值对比)：两样本z 检验时，对比数字是指两组数据均值差，与某个数字进行对比，通常情况下是0（即两组数据平均值差值，与数字0进行对比PK）。

  • 置信水平：指在多大程度上对假设有把握，通常为95%，可选为99%和90%。

  • 假设检验：原假设是等于，小于，还是大于，通常情况下等于（即直接对比是否相等，即是否有差异）。

  • 置信区间表格列出区间估计信息意义较小，通常情况下针对假设检验表格进行分析即可。