-
卡方检验研究X和Y的差异,X和Y均是类别数据。当前需要进一步考虑另一个干扰因素分层项。比如是否吸烟(X)与是否生病(Y)的关系时,将性别纳入考虑范畴(即混杂因素,分层项Factor)。此时则称为分层卡方,也称为Cochran-Mantel-Haenszel检验(CMH检验),分层卡方可很好的解决‘辛普森悖论’问题。SPSSAU支持2*2*K结构数据(即X和Y均为2分类,K层)。
-
-
特别提示:
-
分层卡方时,SPSSAU支持加权和不加权,共两种数据格式,如果有加权项则“加权项”框中下拉选择,如果没有加权项则不用选择。
-
分层卡方案例
-
1、背景
当前有一项关于是否吸烟对于感冒发生风险的影响,共有1046名研究对象,并且记录是否感冒,是否吸烟,以及性别信息。原始数据(模拟数据),如下:
是否吸烟 是否感冒 加权项weight 分层项性别 1 1 465 1 1 2 35 1 2 1 175 1 2 2 25 1 1 1 90 2 1 2 10 2 2 1 164 2 2 2 36 2 1 1 12 3 1 2 11 3 2 1 12 3 2 2 11 3 原始数据使用加权格式,是否吸烟时,数字1表示‘吸烟’,数字2表示‘不吸烟’;是否感冒,数字1表示‘感冒’,数字2表示‘无感冒’。分层项性别时,数字1表示‘男’,数字2表示‘女’,数字3表示‘保密’。加权项weight表示各研究对象类别组合的数量,比如465表示,吸烟且感冒且为男性的数量。
-
另提示:
-
针对分层卡方,SPSSAU支持2*2*k结构,即X和Y均为2个类别,如上述中的是否吸烟和是否感冒,k表示分层项的类别数量,如案例中性别分为‘男’,‘女’和‘保密’,则为3层。
-
-
2、理论
分层卡方是在卡方检验基础上,进一步考虑分层项的干扰(混杂因素),通常分析时需要对于混杂因素(分层项)有一定的预知(或文献参考),然后再进行分层卡方检验。
针对分层卡方,其涉及以下理论知识内容,如下表格:

通常情况下,首先查看‘比值比齐性检验’,如果其呈现出显著性(p 值小于0.05),则说明具有混杂因素,即需要考虑分层项,即分别查看不同分层项下的数据结果。反之如果没有通过‘比值比齐性检验’,即说明没有混杂因素不需要考虑分层项,报告整体的结果即可(包括卡方检验,以及OR值)。
Cochran–Mantel–Haenszel条件独立性用于研究考虑混杂因素(分层项)后,X与Y之间是否还存在着差异关系,相对意义较小。
-
3、操作
本案例使用加权数据格式,放置分析项情况操作如下:
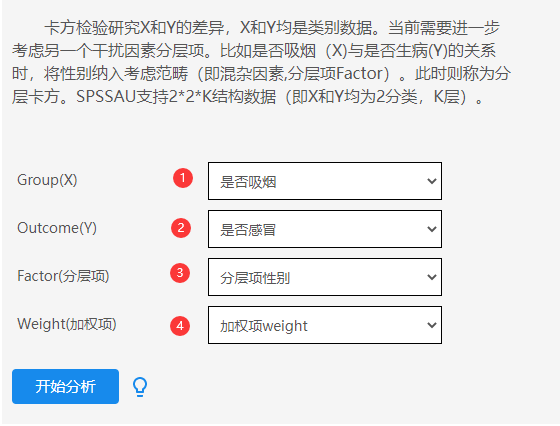
-
4、SPSSAU输出结果
SPSSAU共输出5类表格,如下说明:
表格 说明 Cochran-Mantel-Haenszel test基本说明 分析项的基本汇总。 分层卡方检验汇总表格 √ 展示各层及不分层时,X与Y的卡方检验; √ 使用fisher卡方检验,且展示OR值和95%区间。 Mantel-Haenszel Common比值比OR值估计 展示Mantel-Haenszel Common比值比OR值,以及OR值的对数值,并且展示95%区间。 比值比齐性检验(Breslow-Day-Tarone) 展示Breslow-Day比值比齐性检验。 Cochran–Mantel–Haenszel条件独立性检验 展示chran–Mantel–Haenszel条件独立性检验。 -
5、文字分析
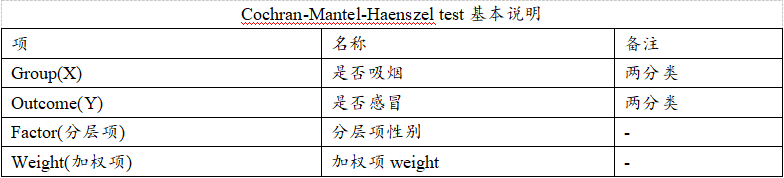
上表格展示放入的暴露因素‘是否吸烟’(X),以及结局因素‘是否感冒’。另分层项为‘性别’,数据使用加权格式,因此放入‘加权项weight’。
-
提示:
-
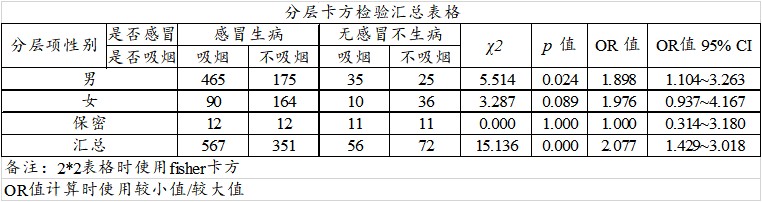
此处OR值计算时是使用较小值/较大值(比如吸烟对应的数字为1,不吸烟对应数字2,则计算时为吸烟/不吸烟)。
上表格展示各个分层(以及不分层)情况下时,各交叉类别项的数据情况,以及输出OR值和fisher卡方值,比如不分层时,即完全不考虑性别时,‘是否吸烟’与‘是否感冒’之间呈现出显著性(χ2=15.136, p =0.000<0.01),OR值为2.077,即说明整体上吸烟是个风险因素,且吸烟时危险度是不吸烟的2.077倍。但是分层考虑时,仅男性时呈现出显著性(χ2=5.514, p =0.024<0.05),而女性和保密两类群体时并没有呈现出显著性( p > 0.05)。也即说明可能需要考虑混杂因素的存在(即分层项存在),接着下面将进行对应的分层项相关检验和说明。
-
提示:
-
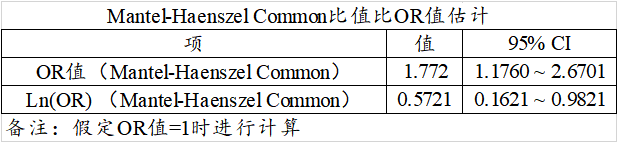
此处95%置信区间的计算是假定OR值=1进行计算。
上表格展示Mantel-Haenszel Common比值比OR值,OR值为1.772,即说明整体上吸烟是个风险因素,且吸烟时危险度是不吸烟的1.772倍(95% CI: 1.1760 ~ 2.6701)。

上表格展示比值比齐性检验,默认使用Breslow-Day法进行检验,上表格显示并没有通过比值比齐性检验(χ2=1.089, p=0. 5801>0.1),即意味着各层之间同质,并不存在混杂作用,即不存在混杂因素(性别),即并不需要分别报告各层对应的值(比如OR值),整体报告即可,此处可报告整体的Mantel-Haenszel Common比值比OR值即1.772。

上表格展示条件独立性结果,Mantel-Haenszel Common法拒绝原假设(χ2=7.0547, p=0. 0079<0.01),也即说明控制混杂干扰因素(性别)之后,吸烟和感冒之间依旧存在着显著性差异,而且OR值为1.772,即吸烟是个风险因素,且吸烟时危险度是不吸烟的1.772倍。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
分层卡方时,SPSSAU支持加权和不加权两种格式,通常使用加权格式,分析时下拉选择‘加权项’即可;
-
比值比齐性检验研究是否存在着混杂因素(即分层项的存在是否具有意义);
-
Mantel-Haenszel Common比值比OR值,与单独进行卡方检验时整体OR值并不一致,Mantel-Haenszel Common比值比OR值可理解为校正OR值,但二者意义一致。
-
