-
ICC组内相关系数是用于研究评价一致性,评价信度,测量复测信度(重测信度)的一种研究方法。比如3个医生(医生1,医生2,医生3)对于同一组患者进行评分,然后判断此3位医生评价结果的一致性水平情况。ICC组内相关系数也用于测量复测信度,比如第一次研究收集100份问卷,然后同样一批被试在1月后再次回答问卷,使用ICC组内相关系数测量复测信度(重测信度)。
ICC组内相关系数用于测量评分数据一致性水平。ICC取值在0~1之间,通常情况下:ICC <0.2则说明一致性程度较差;0.2~0.4之间说明一致性程度一般;0.4~0.6之间说明一致性程度中等;0.6~0.8之间说明一致性程度较强;0.8~1.0之间说明一致性程度很强。
ICC组内相关系数适用于定量数据。除开ICC组内相关系数,还会有另外两个系数分别是Kappa一致性系数和Kendall W协调系数。此三个系数的功能很相似,使用上需要特别注意,具体差异情况如下表所示:
数据类型 功能倾重 其它 ICC组内相关系数 定量 一致性测量 N个数据一致性 Kappa一致性系数 定类(或定序等级数据) 一致性测量 仅针对2项数据一致性 Kendall W协调系数 定量(或定序等级数据) 关联程度测量 N个数据关联程度 首先从数据类型适用性上判断:ICC适用于定量;但是Kappa一致性系数通常用于定类数据一致性;以及Kendall W协调系数用于定量数据,尤其是定序等级数据。
举例场景说明:
场景1:3个医生对于10个病人的智商分值一致性
此类情况可使用ICC,或者Kendall W协调系数,但一般会使用ICC,原因在于定量数据且测量一致性。
场景2:3个医生对于10个病人的疗效(分痊愈,显效,有效,无效)一致性
此类情况可使用ICC,Kendall W协调系数;数据上属于定序等级数据,可使用Kendall W协调系数,当然也可使用ICC。
场景3:2个医生对于10个病人的疗效(分痊愈,显效,有效,无效)一致性
此类情况可使用ICC,Kappa一致性系数,或者Kendall W协调系数;但一般可使用ICC或者Kappa一致性系数且加权。
场景4:2个医生对于10个病人的癌症诊断结果(分阳性和阴性)一致性
此类情况一般会使用Kappa一致性系数,原因在于定类数据且2组(2个医生),定类数据不能使用Kendall W协调系数。
综合上述说明可知,ICC的适用场景相对较多;而Kappa一致性系数主要针对2个相关数据且针对定类数据进行一致性分析;Kendall W协调系数适用于定量数据,且更多倾重于数据关联性研究。
不同专业使用说明:
通常情况下,ICC组内相关系数常见于医学领域,教育学或者心理学相关领域;Kappa一致性系数常用于医学领域,Kendall W协调系数常用于问卷,专家打分一致性判断等。
ICC组内相关系数的使用范围较广,但其复杂度相对较大。需要特别注意数据格式、以及具体ICC模型的选择使用等。假设3个医生对于10个病人智商分值打分,录入后的ICC数据格式如下:
病人编号 医生A 医生B 医生B 1 90 89 87 2 95 98 100 3 89 89 91 4 92 93 91 5 89 91 94 6 80 80 81 7 91 94 93 8 94 92 92 9 84 82 84 10 95 97 96 SPSSAU操作示例如下:
ICC 组内相关系数案例
-
1、背景
3个医生对于10个智障病人进行智商评分;现在希望通过分析研究3个医生的打分一致性水平情况,使用ICC组内相关系数进行研究。录入后的ICC数据格式如下:
病人编号 医生A 医生B 医生B 1 90 89 87 2 95 98 100 3 89 89 91 4 92 93 91 5 89 91 94 6 80 80 81 7 91 94 93 8 94 92 92 9 84 82 84 10 95 97 96 -
2、理论
ICC组内相关系数用于测量评分数据一致性水平。ICC取值在0~1之间,通常情况下:ICC <0.2则说明一致性程度较差;0.2~0.4之间说明一致性程度一般;0.4~0.6之间说明一致性程度中等;0.6~0.8之间说明一致性程度较强;0.8~1.0之间说明一致性程度很强。
ICC一共涉及三个模型,分别如下各表表格所示:
ICC三个模型汇总说明 ICC模型 说明 双向混合 结论针对当前数据,不需要延伸推广到其它研究中;从算法上看,双向混合与双向随机的数字结果完全一模一样; 双向随机 结论需要延伸推广到其它研究中;从算法上看,双向混合与双向随机的数字结果完全一模一样。 单向随机 通常用于测量均值完全相等的程度情况(或者数据记录有遗漏,比如只有评价者数据,但忘记具体那个评价者的打分数据时使用)。 针对上表格特别说明为:双向混合和双向随机模型,从原理角度上进行了区分,但从算法计算的角度上看,其二者的数字计算结果完全一模一样,并没有任何区别。因而在分析时,只需描述选择过程,计算结果上双向混合和双向随机模型的结果完全一致。
另外还涉及一致性和绝对一致性的选择,如下表所示:
ICC之计算类型说明 计算类型 说明 一致性 不考虑误差 绝对一致性 考虑误差 如果研究中考虑系统误差问题,此时需要选择“绝对一致性”计算类型,如果不需要考虑系统误差时,此时选择“一致性”计算类型即可。特别说明一点在于,单向模型只有绝对一致性。
综合上述说明,最终SPSSAU提供出三个选项,分别如下说明:
SPSSAU之ICC选项说明 SPSSAU之ICC选项 说明 双向混合/随机 一致性 结论需要推广延伸,不考虑误差时使用 双向混合/随机 绝对一致性 结论不需要推广延伸,考虑误差时使用 单向随机 绝对一致性 通常用于测量均值是否完全相等。 除此之外:不论是双向混合,双向随机,还是单向随机模型;均会输出单一度量或者平均度量这两个指标值,其区别如下表格:
度量标准选择 度量 说明 单一度量 原始数据 平均度量 原始数据进行过计算,针对计算后数据进行研究 如果说仅针对最原始数据进行分析,应该选择单一度量;如果针对原始数据进行过计算(比如求均值,中位数等),此时应该使用平均度量。
综上所述,结合3个模型,以及计算类型和度量标准,ICC模型一共可分为六个,如下表汇总:
ICC六类细分模型汇总 ICC六类细分模型汇总 简写 说明 双向混合/随机 一致性且单一度量 ICC(C,1) 不考虑误差,且针对原始数据 双向混合/随机 一致性且平均度量 ICC(C,K) 不考虑误差,且针对计算后数据 双向/随机 绝对一致性且单一度量 ICC(A,1) 考虑误差,且针对原始数据 双向/随机 绝对一致性且平均度量 ICC(A,K) 考虑误差,且针对计算后数据 单向随机且单一度量 ICC(1) 测量数据完全相等的程度,且针对原始数据 单向随机且平均度量 ICC(K) 测量数据完全相等的程度,且针对计算后数据 3、操作
3个医生对于10个智障病人进行智商评分,现在希望通过分析研究3个医生的打分一致性水平情况,使用ICC组内相关系数进行研究。本次研究不考虑系统误差,因此使用一致性计算类型,并且3个医生给出的是原始数据非计算后数据,因而使用单一度量标准结果。SPSSAU操作截图如下:

-
4、SPSSAU 输出结果
ICC组内相关系数结果 双向混合/随机 一致性 ICC组内相关系数 95% CI(LL) 95% CI(UL) 单一度量ICC(C,1) 0.921 0.789 0.978 平均度量ICC(C,K) 0.972 0.918 0.992 C表示一致性,1表示单一度量,K表示平均度量 从上表可知:3个医生对10个智障病人进行智商评分,本次研究不考虑系统误差,因此使用一致性计算类型,并且3个医生给出的是原始数据非计算后数据,因而使用单一度量标准结果即ICC(C,1)。从上表可知,最终ICC相关系数值为0.921(95% CI:0.789~0.978),ICC组内相关系数值高于0.9,意味着评价具有高度一致性,也即说明此次3名医生给出的打分有着非常高的可信性,一致性水平非常高。
-
5、文字分析
具体文字分析例子如下:
3个医生对10个智障病人进行智商评分,本次研究不考虑系统误差,因此使用一致性计算类型,并且3个医生给出的是原始数据非计算后数据,因而使用单一度量标准结果即ICC(C,1)。从上表可知,最终ICC相关系数值为0.921(95% CI:0.789~0.978),ICC组内相关系数值高于0.9,意味着评价具有高度一致性,也即说明此次3名医生给出的打分有着非常高的可信性,一致性水平非常高。
-
6、剖析
相对于Kappa一致性系数或者Kendall W协调系数,ICC组内相关系数的适用范围较广,而且可针对双样本或者多样本进行分析一致性。但ICC的分析相对较为复杂,通常需要从三个方面进行分析并且选择最优的ICC模型;分别是模型选择,计算类型和度量标准。
模型选择上,需要考虑是否将当前结论延伸推广到其它研究中,也或者考虑是否为研究数据的绝对相等程度;
计算类型上,如果不需要考虑系统误差则使用“一致性”,如果需要考虑系统误差则使用“绝对一致性”;
度量标准上,如果是原始数据则使用“单一度量”,如果是计算后的数据,则使用“平均度量”。
疑难解惑
-
重复测量方差如何进行重测信度分析?
-
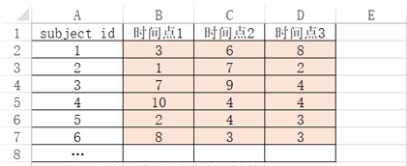
重复测量方差数据如果想测量重测信度,其原理是使用‘ICC组内相关系数’进行分析。首先需要准备好数据格式,比如某个重复测量数据有3个时间点,数据格式类似如下图:
-
Sujbect_id表示被试ID号,但该项并不用放入分析框中。使用SPSSAU进行分析时,将时间点1,时间点2和时间点3放入分析框中。操作类似下图:
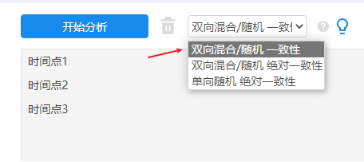
通常情况下选择‘双向混合/随机 一致性’即可,如果考虑测量误差,也可以选择‘双向混合/随机 绝对一致性’,一般不选择‘单向随机 绝对一致性’因此其是用于测量数据是否相等。 最后,在输出结果中,如果说重复测量分析数据是原始数据,那么使用‘单一度量’结果,如果重量测量分析数据是加工过的(比如求过平均值得到),那么使用‘平均度量’结果即可。
