广义估计方程GEE

•  分析方法视频解读： B站 优酷

• 案例数据下载 下载

• 数据格式说明 查看

广义估计方程是一种研究纵向数据（比如重复测量数据，面板数据）的方法。同一测量对象的多次测量数据结果之间很可能有着相关关系，但是常见的研究模型（比如线性回归）要求数据之间独立。因而这违反了数据独立性原则。此时可使用广义估计方程进行研究。

如果是重复测量数据，通常会使用医学研究里面的重复测量方差进行研究，但是重复测量方差要求数据完整不能有缺失，比如有20个研究对象，每个对象进行4次重复测试，那么一定需要20*4=80个数据。但在实际研究中，有缺失数据较为普遍，此时此不能使用重复测量方差进行研究，因而可以使用广义估计方程进行研究。不同的是，重复测量方差是从差异关系角度分析，但广义估计方程是从影响关系角度分析。

除此之外，重复测量方差时，因变量Y只允许为定量连续数据。如果因变量Y的数据分布为二分类，也或者泊松分布数据等，则无法使用，而广义估计方程也能支持。

• • 特别提示：

  • 在重复测量方差分析时，如果出现数据缺失，可使用广义估计方程进行研究；

  • 重复测量方差分析是从差异的角度进行分析，广义估计方程是从影响关系角度进行分析；

  • 重复测量方差时，因变量Y为定量连续数据，自变量X是定类数据；但是广义估计方程时，因变量Y为定量数据或者二分类数据，也或者泊松分布，负二项分布数据均可，以及自变量的数据类型也无特别要求，如果是定类数据直接做虚拟哑变量设置即可。

广义估计方程GEE案例

• 1、背景

  为研究青少年牙齿发育情况与年龄，性别的关系，现收集27名儿童，他们分别在8，10，12，14岁共4个年龄时的牙齿长度指标（distance，垂体至翼上颌裂长度）。现在想研究不同性别儿童牙齿长度指标是否有着明显的差异性。

  明显的，本研究数据为纵向数据即重复测量，同一对象测量了4个年龄段（还有一种纵向数据是比如同一对象测量不同的几个部位），本份数据由于没有缺失数据，因变量为定量数据，因而也可使用重复测量方差进行研究（年龄为组内项）。本案例使用GEE进行研究分析。

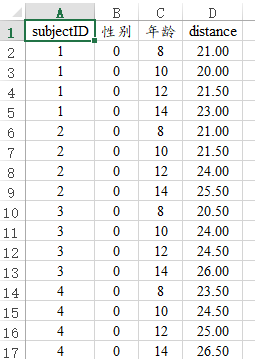
  研究数据结构如下图：

  

  • subjectID：标识具体是哪个研究对象，本次共有27名儿童，编号分别从1~27；

  • 性别：标识研究对象的性别，数字1表示男性，数字0表示女性；

  • 年龄：标识研究对象的测量时间点，分别为8，10，12和14岁这4个时间点进行测量，该项为组内项；

  • distance：牙齿长度指标“垂体至翼上颌裂长度”，该数据为定量连续数据，因此需要使用回归模型。

• 2、理论

  广义估计方程涉及两个点，一是模型的选择，二是矩阵结构。如下图：

  

  • 模型是根据因变量Y的数据分布选择；

  • 如果因变量是定量连续数据，通常使用线性回归模型；

  • 如果因变量的二分类数据，只有数字0或1，那么使用二元Logit或二元Probit回归均可，一般情况下优先使用二元Logit回归，计量研究中使用二元Probit相对较多。

  • 如果因变量服从泊松分布，可使用泊松回归。如果因变量Y的数据特征有点类似泊松分布，但是均值与方差差异较大，则使用负二项回归较好。

  

  • 广义估计方程GEE用于解决数据独立性问题，矩阵结构正是解决此问题的具体方式。

  • 等相关exchangeable：数据之间有着相关性，而且相关性相等，此种情况使用较多。

  • 自相关autoregressive：数据之间有着相关性，而且相邻时间点相关性越大，时间间隔越大相关性越小。

  • 独立independence：数据之间完全独立，同一对象的不同测量数据之间没有关系，此种情况相关于数据完全独立，即数据确实是重复测量，但并没有违反独立性原则。使用较少，但可作为一种探索对比进行分析。

  上述三种矩阵结构如何选择呢？通常的选择办法是分别进行此三种结构时的模型，并且记录下QIC值，QIC值越小，此时就使用对应的矩阵结构模型。 在广义估计方程中，事实上还有其它的矩阵结构，比如M-dependent，Unstructured等，使用相对较少。

• 3、操作

  本例子使用广义估计矩阵模型，由于因变量Y为定量连续数据，因此选择回归模型 ，并且暂使用默认的等相关exchangeable矩阵结构，操作如下图：

  

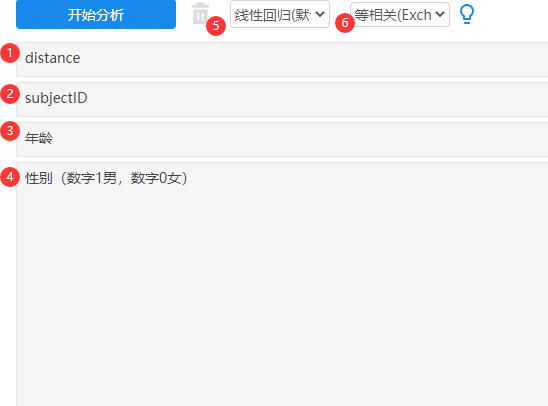
  由于性别使用数字1表示男性，数字0表示女性，已经是哑变量数据，并不需要进行处理；

  年龄作为组内项可放入对应框中，当然不放也可以。

• 4、SPSSAU输出结果

  SPSSAU共输出三个表格，分别是模型基本信息，模型回归系数汇总和边际效应分析结果。

  模型基本信息：描述模型的基本信息，包括每个研究对象subject的测量数量，本案例全部都是4，即都测量了4次；以及链接函数（模型结构），作业相关矩阵（矩阵结构），QIC值等。

  模型回归系数：展示模型的回归值等，结果中的OR值及OR 95%CI值，仅在二元logit，二元probit，泊松回归或负二项回归模型时才有意义；

  边际效应分析结果：此表格在计量研究中使用较多，通常可忽略。边际效应指X变化带来的Y值变化量。

• 5、文字分析

  

  上表格展示模型基本信息，比如本次研究对象为27个，每个对象都有完整的4次重复测量数据，因此测量最小，最大或平均个数均为4。同时展示链接函数（模型结构）为Linear即线性回归模型，作业相关矩阵（矩阵结构）为等相关。QIC值为113.8。

  • 特别提示：

  • QIC值可用于对比不同模型（比如3种矩阵结构时，分别有3个QIC值），此时QIC值越小就选择使用该更优的模型。QICu值和QIC值的意义类似，通常使用其中1个即可。

  

  从上表可知：性别的回归系数值为2.321（z=3.096, p=0.002 <0.01），呈现出0.01水平的显著性，意味着性别会对distance产生正向影响，即相对于女性而言，男性群体的distance牙齿长度明显发育更长。

  • 特别提示：

  • 本次模型的回归模型，因此上表格中的0R值和OR 95%CI值无意义，可直接删除。一般在医学研究中使用二元logit,或者泊松回归也或者负二项回归模型时OR值才有意义，该值为exp(B)即自然对数的回归系数次方。

  

  边际效应指X变化一单位时,Y带来的幅度变化，该指标通常在计量经济研究中使用较多；边际效应结果在计量研究时，而且是使用线性回归时会有一些用处。比如上表格中边际效应dy/dx值为2.321，其代表性别增加一个单位（即从女性变化到男性时），因变量distance牙齿长度增加幅度为2.321。

• 6、剖析

  涉及以下几个关键点，分别如下：

  • 在重复测量方差分析时，如果出现数据缺失，可使用广义估计方程进行研究；

  • 重复测量方差分析是从差异的角度进行分析，广义估计方程是从影响关系角度进行分析；

  • 重复测量方差时，因变量Y为定量连续数据，自变量X是定类数据；但是广义估计方程时，因变量Y为定量数据或者二分类数据，也或者泊松分布，负二项分布数据均可，以及自变量的数据类型也无特别要求，如果是定类数据直接做虚拟哑变量设置即可。