-
Deming回归(也称戴明回归,正交回归),其可用于研究两种仪器(或者两种测量方法等)是否有着一致性(相似的测量值)。Deming回归与普通线性回归(OLS回归)的原理上有所不同,普通线性回归时,只有Y会包含测量误差,但是Deming回归时X和Y均会包含测量误差。普通线性OLS回归和Deming回归相比较,二者均是线性回归范畴,均可以画散点图查看线性趋势情况,但在不满足普通OLS回归假定条件时,使用Deming回归会相对更优。
Deming回归时,其研究两种测量(仪器或方法等)的一致性情况,通常需要输入‘误差方差比值’(误差方差率),具体如何计算‘误差方差比值’(误差方差率),说明见下述理论部分。
-
-
特别提示:
-
Deming回归时,如果不输入‘误差方差比值’,SPSSAU默认该值为1。
-
Deming回归案例
-
1、背景
当前有两家公司的测量仪器(分别称为X和Y),医院希望了解两类测量仪器是否测量一致,分别在60种不同状态下同时对2种仪器进行测量,共得到60行数据。仪器X的测量数据方差值为196.8980226,仪器Y的测量数据方差值为194.9898305。
部分数据如下:
测量仪器X 测量仪器Y 100 100 120 122 132 129 139 136 110 110 110 111 137 137 133 134 140 141 112 112 110 110 120 121 133 131 140 140 119 118 -
2、理论
Deming回归时,需要输入‘误差方差比值’(误差方差率),如果不输入,SPSSAU默认为1,至于如何计算‘误差方差比值’(误差方差率),通常有两种方式。第1种方式是分别计算X和Y的方差值,然后相除即可,计算公式如下:
本案例中仪器X的测量数据方差值为196.8980226,仪器Y的测量数据方差值为194.9898305。因此,具体计算公式可参考案例数据。
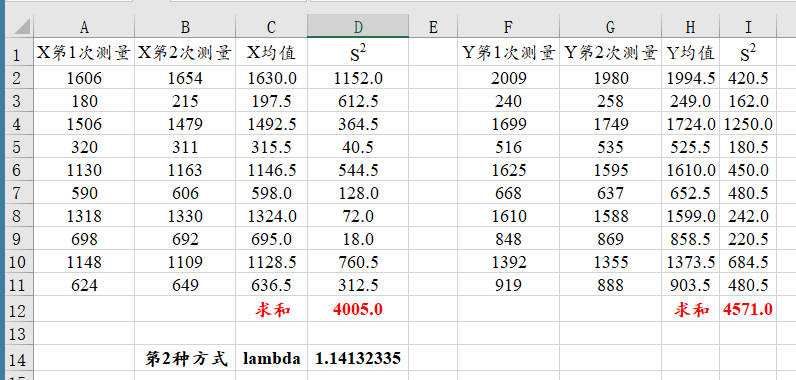
第2种方式是针对X和Y均测量多次,比如X在同一时间点(或同一部位,或同一测量员)测量2次,Y也类似。此时可参考下述公式进行计算。
具体计算类似下图(可参考案例数据文档):
-
至于使用第1种还是第2种方式计算‘误差方差比值’(误差方差率),建议以实际情况为准即可。
-
-
3、操作
本案例操作如下,分别将X和Y放入对应框中,并且输入‘误差方差比值’(误差方差率):
-
4、SPSSAU输出结果
SPSSAU共输出2个表格和散点图,如下说明:
项 说明 回归系数表格 展示回归系数及其95%置信区间等 误差方差表格 此表格仅列出误差方差值,意义极小可忽略 散点图 散点图直观展示数据,且可带趋势线。 -
5、文字分析
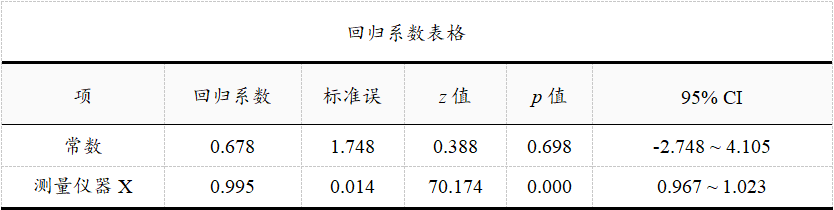
上表格Deming回归分析后的回归系数表格,如果回归系数对应的95%置信区间包括数字1,则说明具有一致性,不存在比例偏差,如果回归系数对应的95%置信区间不包括数字1,则说明不具有一致性,存在比例偏差。从上表格可以看出,测量仪器X的回归系数为0.995,95% CI(0.967~1.023),包括数字1,因而说明测量仪器X和测量仪器Y之间并不存在比例偏差,也即说明两种测量仪器具有测量一致性。
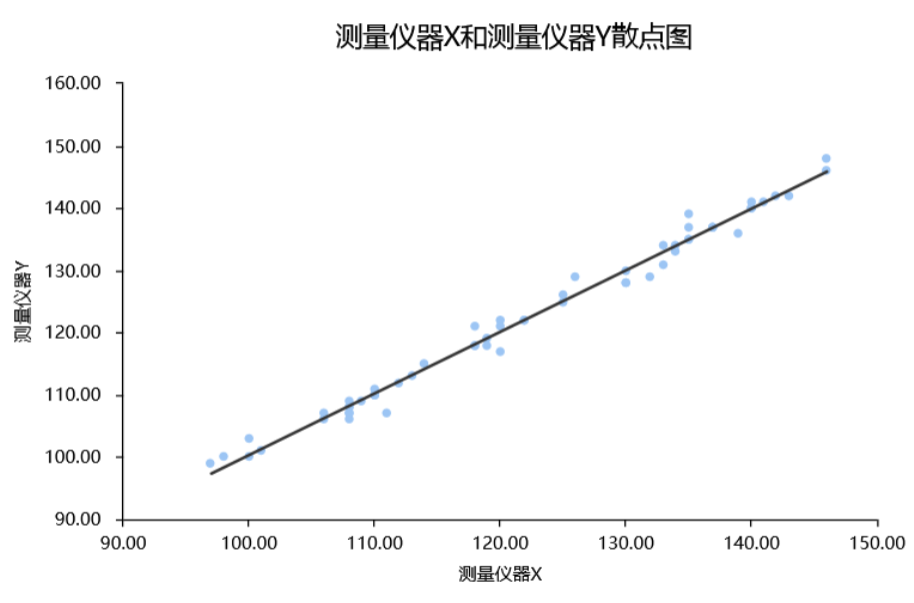
与此同时,也可通过散点图直观查看两个测量仪器的测量一致性,如下图:

-
结合输入的误差方差率,也可单独计算出测量仪器X和测量仪器Y的误差方差值,但该值对于分析基本无帮助可忽略此指标。
-
-
6、剖析
涉及以下几个关键点,分别如下:
-
Deming回归时,‘误差方差比值’(误差方差率)需要事先计算好,然后输入参数,而且其通常有2种计算方式,具体建议以实际情况为准即可。
-
如果不输入‘误差方差比值’(误差方差率),SPSSAU默认为1。
-
测量一致性的研究方法有很多,除Deming回归外,还可选择使用比如ICC,Kappa,Kendall,或者Spearman相关系数等,建议结合实际情况使用即可。
-
Deming回归算法参考文献:[1]孟虹. Deming′s线性回归法在临床检验方法比较研究中的应用[J]. 现代预防医学, 1990.
-
