-
Cox回归模型,又称“比例风险回归模型(proportional hazards model)”,简称Cox回归。它是一种研究相关因素对于生存时间影响的回归模型,其已在医疗,金融和市场研究等专业领域中广泛使用。比如医学研究中,新药物使用是否会有效的增加癌症病人的存活时间;企业创始人能力素质对于企业生存时间的影响关系研究等。
-
当前某研究人员拟观察一种新型癌症药物的疗效情况,首先将50名癌症患者随机分成两组,对照组使用传统治疗方式,实验组使用新式药物治疗方式。并且随访时间为2年。并且以是否死亡为作为结局。希望通过研究了解到新式药物是否对于生存时间带来影响,同时性别和年龄有可能对于生存时间产生影响,因而性别和年龄也考虑在内。
Cox回归的目的在于研究X对于Y的影响,而此处的Y需要使用2项表示,分别为生存状态和生存时间,简单地讲即需要同时考虑结局(死亡)是否发生,同时还需要考虑结局发生的时间。
比如从当前时间点到2年后的随访,有可能患者仅生成4周,也有可能生成20周,更有可能在2年后依然存活,此处的生存时间即为存活的时间长度。同时还需要单独用一项表示生存状态,分别用数字1和0表示,1表示死亡,0表示生存。
需要特别说明的是,结局很可能不是死亡或者存活,很可能会出现两类分别是:“未知状态”和“未确定状态”。“未知状态”:比如失访,某患者失去联系;“未确定状态”:比如2年后的随访时间点时依然存活,那么生存时间最多会记录2年,但事实上生存时间会更长。此两类数据也称“删除censor数据”,录入数据时均录为数字0(即表示“生存”), 可参见下表格:
举例 生存时间 生存状态录入 失访,不知道生存状态 可确定的生存时间,但最终生存状态未知 0 随访时依然稳定 2年(随访时间点) 0 无论删失还是截尾数据,录入数据格式均如上表格即可。通常对于分析影响甚小,但数据录入需要备加注意。
SPSSAU操作示例如下:
-
特别提示,针对Cox回归,需要特别注意以下三点:
-
Cox回归共有两个因变量(一个是生存时间,另外一个是生存状态);缺一不可;
-
“生存状态”项只能为1和0; 1表示死亡,0表示生存;(也或者1表示阳性,0表示阴性;1表示放弃,0表示坚持;诸如此类等等);【可通过SPSSAU的数据编码进行设置成0和1数字】;
-
如果X是定类数据,需要进行虚拟(哑)变量设置。
-
Cox回归案例
-
1、背景
某研究人员拟观察一种新型癌症药物的疗效情况,首先将50名癌症患者随机分成两组,对照组使用传统治疗方式,实验组使用新式药物治疗方式。并且随访时间为2年,以是否死亡为作为结局。希望通过研究了解到新式药物是否对于生存时间带来影响,同时性别和年龄有可能对于生存时间产生影响,因而性别和年龄也考虑在内。
原始数据如下图,下图中药物组别0表示传统治疗,1表示新式药物;性别0表示女性,1表示男性;年龄0表示50以下,1表示50及以上;生存时间以周为单位;生存状态1表示死亡,0表示生存。
药物组别 性别 年龄 生存时间(周) 生存状态 0 0 0 21 1 0 0 0 17 1 1 1 1 12 0 1 1 1 61 0 0 0 0 64 0 0 0 0 7 0 1 1 1 51 1 0 0 0 15 1 0 1 0 2 1 0 1 0 9 1 0 1 0 18 1 0 1 0 17 1 … … … … … -
2、理论
Cox回归是一种研究影响生存时间的方法,由于生存时间数据的特殊性,因而此模型的因变量会涉及两项,分别是生存时间和生存状态;并且生存状态只能使用数字1或者数字0表示(1表示死亡,0表示生存)【可通过SPSSAU的数据编码进行设置成0和1数字】;
-
除此之外,Cox回归会有生存曲线图,此图会非常直观的展示样本的生存情况。
-
针对Cox回归,其自变量的选择通常需要有一定理论依据,不能随意的选择,否则会导致无法计算等问题,并且生存曲线也无法有效展示生存情况等。以及如果自变量中有定类数据,需要首先进行虚拟(哑)变量设置【回归分析涉及定类数据时,均需要进行虚拟哑变量设置】。
-
-
3、操作
本案例研究药物对于癌症患者存活时间的影响关系,SPSSAU操作截图如下:

-
4、SPSSAU输出结果
Cox回归模型似然比检验结果 似然比卡方值 df
p
8.725 3 0.033 上表格为模型似然比检验结果,似然比检验原假设为是否放入自变量两类模型质量均一致;从上表可知,模型拒绝原定假设(χ2=8.725,p =0.033 <0.05),即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。
Cox回归模型分析结果汇总 项 回归系数 标准误 z 值 p 值 HR值 HR值95% CI(LL) HR值95% CI(UL) 药物组别 -1.171 0.453 -2.587 0.010 0.310 0.128 0.753 
-
Cox回归模型分析步骤一般分三步
-
第一步:对模型整体情况进行描述说明,以及列出模型公式;
-
第二步:逐一分析X对于Y的影响情况;如果X对应的p 值小于0.05则说明X会对Y产生影响关系,此时可结合HR值进一步分析影响幅度。
-
第三步:总结分析结果。
从上表可知,将药物组别作为自变量进行cox回归研究,模型公式为:ln[h(t,X)/h0(t)]=-1.171*药物组别 (ln代表取对数,h0(t)代表基准风险率)。最终具体分析可知:药物组别的回归系数值为-1.171,并且呈现出0.01水平的显著性(z =-2.587,p =0.010 < 0.01),意味着药物组别会对生存事件产生显著的负向影响关系。以及相对危险度(HR值)为0.310(95% CI:0.128~0.753),意味着相对于传统治疗,新式药物的死亡风险为传统治疗的0.310倍。
-
特别提示
-
针对模型公式部分:ln[h(t,X)/h0(t)]=-1.171*药物组别 (ln代表取对数,h0(t)代表基准风险率); h0(t)代表基准风险率,此为Cox回归模型结构,涉及算法原理,建议用户可查阅相关书籍,或者暂忽略理解。
-
针对影响关系上:此处p 值小于0.05且回归系数为-1.171 < 0,意味着有着显著性负向影响;即相对传统药物,新式药物会对生存状态产生负向影响,生存状态1代表死亡0代表生存,那么此处意味着:相对传统药物,新式药物患者更容易存活的意思。【负向影响可理解为,X越大Y越小即 越使用新式药物,越容易存活】
除此之外,Cox回归会生成生存曲线如下图分析:
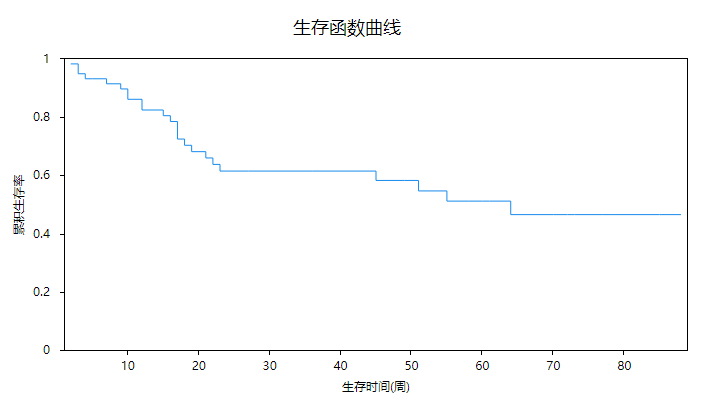
上图看出,X轴为生存时间,Y轴为累积生存率。生存时间为0即刚开始时,累积生存率为1,即均为存活状态;随着生存时间的增加,累积生存率也会明显的下降,尤其是0~20周这段时间;但是在20~45周之间时,生存率基本不会变化,意味着20~45周死亡率基本为0;另外45~65周之间时,死亡率也会明显的下降,说明这段时间也有着较高的死亡率。但约在65周之后(65周~到140周随访2年),死亡率保持稳定,即说明65周~140周这段时间内死亡率稳定。
另外,如果还希望将年龄纳入模型考虑范畴中(即作为控制变量),希望对比不同年龄组别样本时,生存曲线的差异情况,此时可将年龄放入“分层项”框中,并且得到下图。
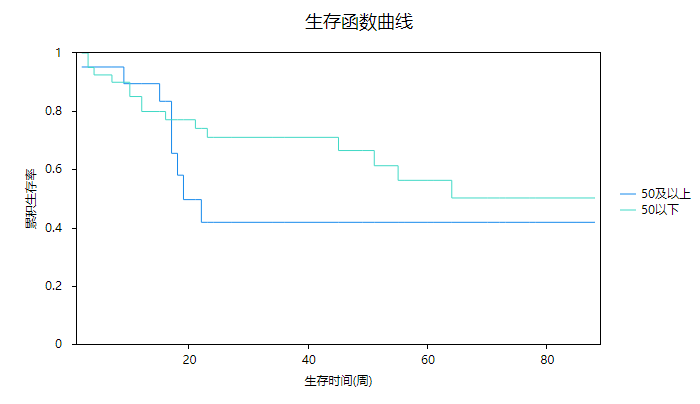
上图可以明显的看出,对于50以下的患者,从大约22周后,其累积生存率保持稳定,即说明大约22周后,50以下的患者会保持稳定的存活状态;而且在约18周后,50及以上的患者累积生存率会明显的高于50以下的患者,意味着过了18周后,50及以上的患者存活率明显更高。
如果还希望分析不同性别患者的生存曲线对比,也可类似进行分析即可。
-
-
5、文字分析
具体文字分析例子如下:
本研究数据针对50名癌症患者进行研究,将50名患者随机分为两组,分别是实验组和对照组,实验组使用新式药物,对照组使用传统药物;对于研究病例进行2年后随访。使用SPSSAU软件进行分析,利用Cox回归方法进行研究。
从上表可以看到,模型拒绝原定假设(χ2=8.725,p =0.033 <0.05),即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。模型公式为:ln[h(t,X)/h0(t)]=-1.171*药物组别 (ln代表取对数,h0(t)代表基准风险率)。
药物组别的回归系数值为-1.171,并且呈现出0.01水平的显著性(z =-2.587,p =0.010 <0.01),意味着药物组别会对生存事件产生显著的负向影响关系。以及相对危险度(HR值)为0.310(95% CI:0.128~0.753),意味着相对于传统治疗,新式药物的死亡风险为传统治疗的0.310倍。
针对生存曲线分析可知,随着生存时间的增加,累积生存率也会明显的下降,尤其是0~20周这段时间;但是在20~45周之间时,生存率基本不会变化,意味着20~45周死亡率基本为0;另外45~65周之间时,死亡率也会明显的下降,说明这段时间也有着较高的死亡率。但约在65周之后(65周~到140周随访2年),死亡率保持稳定,即说明65周~140周这段时间内死亡率稳定。
对比不同年龄患者的生存曲线可知:对于50以下的患者,从大约22周后,其累积生存率保持稳定,即说明大约22周后,50以下的患者会保持稳定的存活状态;而且在约18周后,50及以上的患者累积生存率会明显的高于50以下的患者,意味着过了18周后,50及以上的患者存活率明显更高。
-
6、剖析
-
特别提示,针对Cox回归,需要特别注意以下几点:
-
Cox回归共有两个因变量(一个是生存时间,另外一个是生存状态);缺一不可;
-
“生存状态”项只能为0和1;1表示死亡,0表示存活;(也或者1表示阳性,0表示阴性;1表示放弃,0表示坚持;诸如此类等等);【可通过SPSSAU的数据编码进行设置成1和0共两个数字】;
-
如果X是定类数据,需要进行虚拟(哑)变量设置;
-
Cox回归的模型涉及算法原理,建议可忽略可查看相关书籍内容;
-
生存曲线可直观展示生存时间与生存率之间的关系,建议详细对比分析。
-
疑难解惑
-
PH假定检验是什么意思?
-
通常情况下,Cox回归模型希望满足PH假定,即p 值需要大于0.05,如果某项有违反,即p 值小于0.05,此时可考虑将该项放入分层项中分析,以解决PH假定检验问题。
-
如何画图?
-
如果有定类的X数据,将其放入对应框中,SPSSAU默认针对定类数据画生存图。并且默认提供整体的生存图。
-
HR值和RR值的区别?
-
SPSSAU中COX回归或者kaplan-meier曲线时,HR值和RR值的计算公式均一致,计算公式为exp(b),即自然对数的回归系数次方。该两个指标在实际研究中意义可能有所不同,但数学计算公式完全一致。
-
p for trend这个指标如何计算?
-
p for trend指标是指某个X对于Y的影响时的趋势情况如何。实际研究中计算该指标,其步骤如下:
-
第1步:对X进行分组处理得到新的标题Xnew,比如预期将血压分为低、中和高共三组:
-
第2步:对Xnew中的组别赋值编码数字,比如低赋值编码为0,中为1,高为2(此种方式为常见的编码方式,当然也可使用低/中/高组分别的中位数作为赋值编码数字);
-
第3步:将Xnew纳入模型中,其对应得到p值即为p for trend指标。
-
原理上:即将X分成几个组别,并且用不同的数字标识出各个组别的相对大小后得到分组后的Xnew,这样Xnew只包括几个数字且数字代表各个等级组别,此时将Xnew纳入模型时,其得到的p 值即为p for trend。
-
另提示:将X进行分组和编码,建议可使用SPSSAU数据处理-》数据编码功能实现,也或者在EXCEL中处理。
-
Cox回归时回归系数如何解读?
-
Cox回归研究X对于生存事件的影响,从数学理论上,Cox回归是基于HR(Hazard ratio,风险比或危险率)概念进行研究,其研究‘生存风险’的影响。
-
如果某X的回归系数>0且显著,此时X对于生存风险有正向影响,可理解为X越大时生存时间相对更短,以及回归系数>0时HR值>1,即为风险因素,比如HR为2,其意义为X增加一个单位时,阳性事件发生的风险概率加大2倍。
-
如果某X的回归系数<0且显著,此时X对于生存风险有负向影响,可理解为X越大时生存时间相对更长,以及回归系数<0时HR值<1,即为保护因素,比如HR为0.2,其意义为X增加一个单位时,阳性事件发生的风险概率减少0.2倍。
-
如果某个X的回归系数=0(即不显著时认为其无法明显偏离0),即X对于生存时间无影响,此时HR值为1,即无关因素。
-
回归分析时某X标准误特别小或者特别大,也或者出现null值?
-
如果出现此类现象,通常是共线性问题所致,建议使用进阶方法模块里面的共线性分析,然后按照SPSSAU智能分析建议进一步处理即可。
-
Cox & Snell R 方和Nagelkerke R 方为Null值?
-
从计算公式上看,该两个指标会取指数次处理,指次数为2/n,n为样本量,当样本量较大时,该两个指标容易出现计算结果为null的情况。建议使用McFadden R 方值即可。
-
保存生存函数和保存风险函数?
-
选中保存生存函数时,系统会新生成标题,名称类似为:Life_Function_1234用于标识生存函数预测值。类似地,选中保存风险函数时系统也会新新生成标题,名称类似为:Risk_Function_1234。与此同时,风险函数 = 1-生存函数。新生成的标题可用于进一步分析使用,比如校准曲线,NRI/IDI等。
-
C-index即C指数(C统计量)?
-
COX回归时默认输出C指数及其95%置信区间值,该指数是一个综合性指标,其用于评估Cox回归模型的预测能力情况,一般情况下,该指标会介于0.5~1之间,如果该值为0.5则意味着模型没有预测能力,如果该值为1则意味着预测与实际情况完全一致,通常情况下该指标介于0.5~0.7则意味着预测能力一般,介于0.7~0.8意味着预测能力较强,介于0.8~0.9意味着预测能力强,大于0.9意味着预测能力非常强。需要提示的是,如果使用Cox回归研究影响关系,此时通常不用关注该指标值。
-
如果是二元logit回归希望进行预测能力判断,研究者可使用ROC曲线得到AUC值(使用联合诊断),该值即为C指数值,具体可查阅ROC曲线帮助手册。
